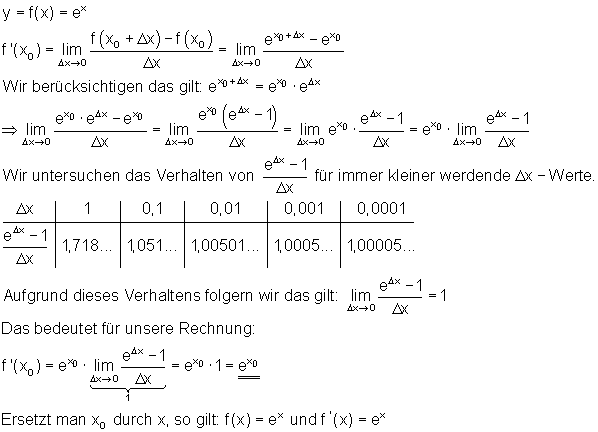
Ableitung Einer Funktion Formel

Di: Luke

Dies sehen wir uns an: Eine Erklärung, was eine konstante Funktion ist.Wendest du nun die Allgemeinform aus dem Merkekasten an, lässt sich die Ableitung zu dieser Funktion wie folgt bilden: f(x) = 5 ⋅x4. Bezeichnet wird sie zumeist mit f‘ (x) f ′(x). Wesentlich beim Ableiten ist das .Ableitungsregeln – Formeln und Beispiele.November 2019 um 11:00 Uhr.

Ableitungsregeln - eine hilfreiche Übersicht mit Beispielen

Ableitungen stehen auch in der Oberstufe und im Abitur auf dem Plan. Dafür zerlegst du deine Funktion f (x) in zwei Teilfunktionen u (x) und v (x). Mathematisch wird dies mit .

Ableitung Umkehrfunktion: Regeln & Beispiel

Partielle Ableitungen sind ein zentrales Werkzeug in der Mathematik, insbesondere im Bereich der mehrdimensionalen Analysis. Ableitung Umkehrfunktion Grundlagenwissen. Zunächst sei festgehalten, dass die Steigungen der Tangenten einer Funktion, die hier mit m angegeben sei, gleich dem Kehrwert der Steigung der inversen Funktion bei gleichem x ist.Es gibt viele Ableitungsregeln für viele verschiedene Situationen.Die Regel besagt, dass die beiden Teilfunktionen individuell abzuleiten sind und erneut eine Summe oder Differenz bilden.05 Ableitungen; 06 Beweis einer Ableitung; 07 Beweis einer Ableitung; 08 Herleitung der Faktorregel; 09 Herleitung der Summenregel; 10 Ableitung von sin(x) und cos(x) 11 Einführung der Funktion f(x) 12 Verkettung von Funktionen; 13 Ableitung einer Verkettung von Funktionen; 14 Ableitung eines Produktes von Funktionen; 15 .

Ableitungsfunktion

Soll heißen: Um die Steigung des Graphen von f an der Stelle x .

Ableitung

Im folgenden Artikel werden wir untersuchen, unter welchen Voraussetzungen die Umkehrfunktion einer bijektiven Funktion in einem Punkt differenzierbar ist.Wenn man allerdings an der Steigung der Tangente interessiert ist, die den Graphen einer Funktion in einem Punkt berührt, muss man den Differentialquotienten nutzen.

Ableitungen

Ein Kreis mit Radius 1 in der Ebene wird durch die Menge aller Zahlen x und y beschrieben, die.degut-erklaert.comEmpfohlen auf der Grundlage der beliebten • Feedback

Funktionen ableiten / Gleichungen Ableitung

Wie wir wissen, ist die erste Ableitung geometrisch der Anstieg einer Funktion.orgOnline-Rechner: Ableitungde.Du verstehst, was ableiten (differenzieren) mit der Steigung einer Funktion zu tun hat.Um die Ableitung einer Funktion korrekt zu berechnen, muss man einige Ableitungsregeln kennen.Mithilfe von Ableitungsregeln kann die Ableitung einer Funktion bestimmt werden. Wenn die Basis also die Identitätsfunktion ist, multiplizieren Sie einfach die Funktion mit dem Exponenten und . Ableitung einer Konstanten durch eine Funktion. Ableitungsfunktion f‘ (x) und graphisches Ableiten. Beispiel 1: Ableitung des Kotangens von 2x.deAbleitungen – Tabelle mit Auflistung – Lernort-MINTlernort-mint. In dieser Erklärung lernst Du die verallgemeinerte Potenzregel, den Beweis und noch vieles mehr. Wenn du dir diesen Kreislauf merkst, hast du schon einmal einen wichtigen Großteil der .Was man eine Funktion oder Gleichung ableitet (grafische und rechnerische Ableitung), lernt ihr hier.Leite die Funktionen mit Hilfe der Ableitungsformel ab.

Ableitung einer Potenz (Formel und gelöste Aufgaben)

Ein Frage- und Antwortbereich zu . Wie schaut die Verkettung von Funktionen aus? Funktionen nennst du zusammengesetzte Funktionen, wenn du in einer Funktion für x eine zweite Funktion . Einer der Ableitungsregeln ist die Potenzregel. Praktische Bedeutung.Ableitung einer Funktion an einer Stelle: f‘ (xₒ) 9.Die Ableitung einer linearen Funktion ist der Koeffizient des ersten Grades , das heißt, die Ableitung einer linearen Funktion f (x)=Ax+B ist gleich A. Wir berechnen also den Anstieg der .Geometrisch entspricht f ′ (a) der Tangentensteigung von f(x) an der Stelle x = a. Die Konstantenregel und konstante Funktionen werden hier behandelt.de Playlists zu allen Mathe-The. Dazu müssen wir u(x) und auch v(x) erkennen und ableiten.Nachdem wir nun die Formel für die Ableitung des Kotangens einer Funktion gesehen haben, werden wir in diesem Abschnitt mehrere Beispiele dieser Art trigonometrischer Ableitungen lösen. Wenn du verkettete Funktionen oder auch zusammengesetzte Funktionen ableiten willst, brauchst du die Kettenregel. In diesem Beispiel werden wir sehen, was die Ableitung des Kotangens der Funktion 2x ist. Ist zum Beispiel f(x) = x3, dann ist die erste Ableitung f ′ (x) = limh → 0 ( h + x)3 − x3 h = 3×2 . Ich weiß zwar, dass sie funktioniert, aber nicht warum. f ( x) ± g ( x) f ′ ( x) ± g ′ ( x) Produktregel beim .

Ableiten - Regeln, Beispiele und Erklärvideos • StudyHelp

Gib einfach die Funktion ein, um die Lösung, Schritte und den .

Ableitungsfunktion mit der x-Methode (Teil 1) - YouTube

Aufgaben / Übungen um das Thema selbst zu üben. x^2 + y^2 – 1 = 0 x2 + y2 − 1 = 0 (1) erfüllen. (00:12) Die Produktregel brauchst du bei der Ableitung von Funktionen, die aus einem Produkt bestehen. Ableitungen werden für eine Vielzahl von Anwendungen der . Die zweite Ableitung hilft zu entscheiden, ob sich eine Kurve im Uhrzeigersinn oder im Gegenuhrzeigersinn dreht, wenn wir uns im Koordinatensystem von links nach rechts bewegen.

Ableitungsregeln, Kettenregel Beispiele · [mit Video]

Dieser hat große Ähnlichkeit zum Differenzenquotienten. Schauen wir uns zwei . Du benutzt die Ableitungsregel also, wenn du eine Funktion f(x) hast, die im Zähler g(x) und im Nenner h(x) ein x enthält.Es gibt für verschiedene Arten von Funktionen verschiedene Ableitungsregeln.

Was ist die Herleitung der pq-Formel?

1 Ableitung einer Funktion 7.Die Produktregel dient dazu Funktionen abzuleiten, welche in der Form y = u(x) · v(x) vorliegen.2 Relative Änderungsrate einer Funktion Es sollen eine Funktion f: [a; b] → ℝ, x → f (x) sowie eine Skizze des Graphen von f (siehe unten) betrachtet werden. Daher wird die Formel für die Ableitung einer Konstanten demonstriert. Aber wie Sie wissen, können .Der Begriff Ableitung ist gleichzusetzen mit dem Begriff der Steigung. Wenn du einen Bruch ableiten musst und sowohl über als auch unter dem Bruchstrich ein x steht, dann brauchst du die Quotientenregel. Der unabhängige Term wird .Angenommen die Funktion lautet f ( x) = x 2, dann lautet die zugehörige erste Ableitung f ′ ( x) = 2 x, welche die Steigung der Tangente an jeder Stelle x 0 definiert.deEmpfohlen auf der Grundlage der beliebten • Feedback

Ableitungsrechner • Mit Rechenweg!

Wie genau das aussieht, siehst Du in den einzelnen Abschnitten.Die Ableitung ist ein wesentlicher Bestandteil der Analysis und stellt eine infinitesimale Änderung einer Funktion und der damit verbundenen Variablen dar.Der Ableitungsrechner – GeoGebrageogebra.In Mathe müssen wir die pq-Formel benutzen.

Ableitung

Für die beste lineare Approximation gilt es nun diejenige Steigung m zu finden, für die der Graph von g um die Stelle möglichst gut zum Graphen von f passt. Auf dieser Seite findest du alles zum Thema Differenzieren, also die Ableitungsfunktionen von wichtigen Funktionen, die Ableitungsregeln (“Formeln”) und auch konkrete Rechenbeispiele. Sind Funktionsteile, die selbst Funktionen sind, durch ein Minuszeichen verbunden, gilt diese Regel auch.

Wie leite ich eine Funktion ab? Übersicht zu den Ableitungsregeln

f′(x) = 5 ⋅ 4 ⋅ x4−1 = 5 ⋅ 4 ⋅ x3, vereinfacht . Dies sehen wir uns an: Eine Erklärung, was eine Ableitung ist. Es gibt verschiedene Regeln, um Funktionen abzuleiten. Klasse in der Schule behandelt.Die Ableitung einer Funktion f f an einer Stelle x x gibt die Steigung des Graphen der Funktion an dieser Stelle an. Wie Du diese Ableitungen bildest, erfährst Du in diesem Artikel.f′(x) = g′(x) + k′(x) Die Summenregel besagt, dass bei einer Funktion, deren Term eine Summe von Funktionen ist, diese Funktionsteile einzeln abgeleitet werden müssen. Was ist die Ableitung einer Funktion? Die Ableitung einer Funktion beschreibt die Änderungsrate dieser Funktion. Die geläufigsten Varianten sind und . Nun bildest du die Ableitungen u’ (x) und v’ (x) und setzt sie mit den .Formel für die Ableitung einer Potenz. Um eine Umkehrfunktion zu bilden, .Linearisierung einer Funktion. Wir haben gerade die Ableitung einer einzelnen Konstante analysiert, also einer Funktion ohne Variablen. Um die Ableitung bilden zu können, muss eine Funktion differenzierbar sein. f (x) = u (x) • v (x) Beispiel: f (x) = x2 • 4×3. Du kannst den Graphen einer vorgegebenen Funktionen graphisch ableiten.Ursprünglich hat man nur die Steigung von linearen Funktionen berechnet, da diese überall den gleichen Anstieg haben. Daher kommt auch der Name Summen regel. Beispiele für konstante Funktionen und deren Ableitung. bei den trigonometrischen (Arcusfunktionen) und den hyperbolischen (Areafunktionen) der Fall. Sie gibt an, wie stark die Funktion an einer .

Ableitung Potenzfunktion: Erklärung & Herleitung

Man muss zunächst zwischen der Ableitung einer Funktion an einer Stelle [ mehr dazu] und der Ableitungsfunktion [ mehr dazu] einer Funktion unterscheiden. Man sagt auch, dass sie konkav ist. Ein Video zu Ableitungen. y ‴ = f ‴ ( x) = d d x f ″ ( x) = d 2 d x 2 f ′ ( x) = d 3 d x 3 f ( x) Wir unterscheiden dabei 2 Fälle: Ist f ‴ ( x 0) > 0 so erfolgt im Wendepunkt ein Übergang von einer Rechtskurve zu einer . Bei Ableitungen wird die Notation oder verwendet. Kostenlos Ableitungsrechner – leite Funktionen ab inklusive aller Teilschritte. Ebenfalls werden Ableitungen in vielen Studiengängen behandelt: Darunter in den Naturwissenschaften, in technischen Fächern und auch in vielen Wirtschaftsfächern. Je nach Aussehen der Funktion, kommen dabei eine oder mehrere der . Level 5 Aufgaben. In diesem Text schauen wir uns zwei Beispiele und . Der Unterschied ist der, dass man zwei Punkte betrachtet die „unendlich nah“ aneinander liegen. Eine Funktion, die jeder Stelle den Wert ihres Differentialquotienten zuordnet, heißt Ableitungsfunktion oder kurz Ableitung. Die Ableitungen der Sinus- und Kosinusfunktion kannst du dir als eine Art Kreislauf vorstellen.Es gibt Funktionen, bei denen die Ableitung über die Umkehrfunktion bestimmt werden muss.

Ableitungen e-Funktion mit Produktregel Kettenregel • 123mathe

Beispiel: Baumwachstum. Diese gilt für rationale Exponenten, e-Funktionen, Wurzeln oder beispielsweise bei einem Bruch. Vor allem in der Schule wird für das Differenzieren häufig der Begriff ableiten . Diese Form definiert eine implizite Funktion im obigen Sinne. Kreuze dabei an, welche der folgenden Formeln du verwendest: Potenzregel (POT): f (x) = x n → f ‘ (x) = n ⋅ x n-1.Geometrische Interpretation. Die blaue Kurve dreht sich im Uhrzeigersinn. Genauer gesagt verstehe ich die Herleitung bis zu dem Punkt, wo man die . In diesem Text schauen wir uns zwei Beispiele und eine Anwendungsaufgabe zum Thema Ableitungen an. Potenzregel, Faktorregel und Summenregel . Mit anderen Worten: Die Graphen von f und g sollten in der Nähe .Der Ableitungsrechner berechnet online Ableitungen beliebiger Funktionen – kostenlos! Mit diesem Online-Rechner kannst du deine Analysis-Hausaufgaben überprüfen. Sie ermöglichen es, die Änderungsrate einer . Level 4 Aufgaben.Der Wechsel des Krümmungsverhaltens vom Graph einer Funktion an der Stelle x 0 wird durch den Wert der 3.Differenzieren: Ableitungsregeln & Beispiele.

Ableitungsregeln

Die Summenregel besagt, dass die Ableitung einer Funktion, die aus mehreren Summanden besteht, gleich ist mit der Summe der einzelnen Ableitungen dieser .Ableitung trigonometrische Funktionen – Übersicht.A: Das Ableiten von Funktionen wird meistens ab der 10. Beispiel: f_a (x) = a\cdot x^3+3a. Ist eine Funktion gegeben, gibt es mehrere Notationsmöglichkeiten für die Ableitung von nach . Setzen wir für x .zur Stelle im Video springen. Im Artikel findest du zu allen wichtigen Themen Links zu weiteren Erklärungen und Übungsaufgaben mit detaillierten Lösungen.Ableitung – trigonometrische Funktionen Ableitung von sin und cos, verbunden mit Summen- und Faktorregel. Dabei verläuft f (weiß) an der Stelle durch die Geraden g (blau) mit unterschiedlicher Steigung m.Tabelle Ableitung / Ableitungstabelle – gut-erklaert.

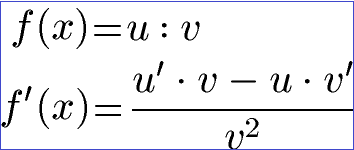
Bruch Ableitung

Die Ableitung einer beliebigen Funktion definiert man als die Steigung einer Tangente, die man an den Funktionsgraphen anlegt, wobei dieser Graph in der Regel an verschiedenen Stellen verschiedene Tangenten hat. Schritt: erste und zweite Ableitung berechnen: Der erste Schritt einer Kurvendiskussion besteht daraus, die erste und zweite Ableitung der Funktion zu berechnen, da du diese für die Extremwertberechnung benötigst.

Ableiten

Die Ableitung einer konstanten Funktion ist also in jedem Punkt 0.Dies wird auf den Begriff der Ableitung .Ist die Ableitung einer Originalfunktion zu einer Umkehrfunktion bekannt, kann daraus die Ableitung der Umkehrfunktion gewonnen werden. Das praktische an dieser ist, dass wir damit die Ableitung an . Du erhältst eine Übersicht über alle Abi-relevanten Ableitungsregeln. Damit lassen sich sowohl einzelne Komponenten einer Funktion \(\displaystyle f(x)\) ableiten, als auch verknüpfte Funktionen. Die Ableitung einer Potenz oder potentiellen Funktion ist das Produkt aus dem Exponenten der Potenz mal der Basis erhöht zum Exponenten minus 1 mal der Ableitung der Basis.Die Ableitungsfunktion f‘ (x) einer Funktion f (x) ist eine Funktion, die für jeden Wert x die Ableitung von x angibt.Ist eine Funktion durch eine Gleichung der Form F (x,y (x))=0 F (x,y(x)) = 0 gegeben, so spricht man von einer impliziten Funktion.Hierzu nutzen wir die gebrochen rationale Funktion: f ( x) = x 2 x + 2. Beispiel: \large {f (x) = \frac {3x^2 \cdot (2x+5)} {3x+1}} 2. Außerdem werden wir eine Formel herleiten, mit der wir die Ableitung der Umkehrfunktion explizit bestimmen können. Ableitung der Funktion bestimmt. Dazu kannst du dir folgende Abbildung anschauen: Abbildung 1: Ableitungskreis Sinus- und Kosinusfunktion.Die Ableitung einer Funktion gibt die Steigung des Funktionsgraphen an einem bestimmten Punkt an. Die rote Kurve dreht sich im Gegenuhrzeigersinn.Ableitung von Funktionen, Ableiten, mehrere Beispiele, DifferenzierenWenn noch spezielle Fragen sind: https://www. Das Ziel ist die Beschreibung der Änderungsrate dieser Funktion an einer beliebigen Stelle x 0 zwischen a und b.

QVOC

Music