QVOC

Additionstheoreme Winkelfunktionen

Di: Luke

Besonders bei der mathematischen Beschreibung von Schwingungsvorgängen wird häufig von Winkelfunktionen, speziell der Sinusfunktion mit Gleichungen der Form y = f ( x ) = a ⋅ sin ( b x + c ) Gebrauch gemacht. Für Sinus und Kosinus lassen sich die Additionstheoreme aus der Verkettung zweier Drehung um den Winkel bzw.Subtraktion) folgt.Additionstheoreme [ Bearbeiten] Doppelwinkelfunktionen [ Bearbeiten] Winkelfunktionen für weitere Vielfache [ Bearbeiten] Rekursionsformeln mit : .comEmpfohlen auf der Grundlage der beliebten • Feedback

Formelsammlung Trigonometrie

Die Bezeichnung . Die Additionstheoreme für Winkelfunktionen sind Formeln, mit denen du die Funktionswerte der trigonometrischen Funktionen (Sinus, Cosinus, Tangens) von Summen . (01:24) Schauen wir uns die Sinus, Cosinus und Tangens Formeln nochmal an zwei konkreten Beispielen an: Beispiel 1: Mit den Winkelfunktionen Sinus, Cosinus und Tangens kannst du nicht nur Winkel berechnen. diese Werte für 50° bestimmt werden sollen, dann geht man an diesen Winkel in kleinen Schritten von beispielweise 0,1° vom Winkel 0,1° ausgehend heran.Als Additionstheoreme für Winkelfunktionen werden Formeln bezeichnet, durch die die Funktionswerte von Summen und Differenzen von Winkeln auf die Werte der . Es ist allerdings auch möglich, ausgehend von der Definition dieser Funktionen am Einheitskreis die zu einem Winkel als Abszisse eines Graphenpunktes gehörende Ordinate sofort aus . In: Mathematik für die Fachschule Technik. Ein Punkt P werde nach einer Drehung um α noch einmal um einen Winkel β gedreht.zur Stelle im Video springen. Theoretisches Material, Tests und Übungen Additionstheoreme für Winkelfunktionen, Trigonometrie, 9.Winkelfunktionen am Einheitskreis Betrachtet man die Winkelfunkionen ausschließlich im rechtwinkeligen Dreieck, dann beschränken sich die Winkel auf den Bereich zwischen 0° und 90°. Für die Summen bzw. Das rechtwinkelige . Summensatz Winkelfunktionen. Wenn wir die Formeln umstellen , können wir auch die Längen der Dreiecksseiten berechnen. sin(x) – sin(y) = 2 · cos( ) · sin( ) cos(x) – cos(y) = –2 .

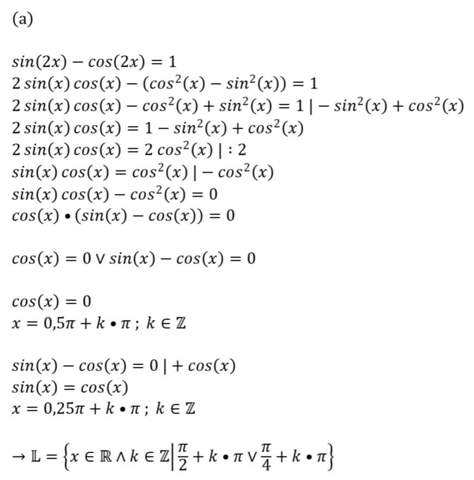
Ein allgemeines Verfahren zur direkten Bestimmung der Lösung oder der Lösungen einer goniometrischen Gleichung gibt es nicht, – oft sind die Lösungen nur durch Näherungsverfahren zu ermitteln.

Additionstheoreme sind Formeln zur Vereinfachung von Winkelfunktionen der Form: \(\sin(\alpha\pm\beta)\), . Nachfolgend die Betrachtung der Winkelfunktionen am Einheitskreis, also einem Kreis mit dem Radius r=c=1, wodurch die trigonometrischen Funktionen für .Das wohl wichtigste Werkzeug bei der Umwandlung und Vereinfachung trigonometrischer Ausdrücke sind die Addititonstheoreme für Sinus und Kosinus: Als .Winkelfunktionswerte, Beziehungen.deSinus, Kosinus & Tangens ⇒ einfach & verständlich erklärtmathe-lerntipps.Alternativ folgen die Additionstheoreme aus der .1 Die Additionstheoreme und funktionales Denken 137 Mentally (or physically) constructing a standard right triangle containing an angle of 20 , and then comparing the length of the side of this triangle opposite to the 20 angle with the length of its hypotenuse, noting that the former length is considerably shorter than the latter, perhaps by a ratio of . Differenzen trigonometrischer Funktionen können Produktdarstellungen angegeben werden, die für das praktische Rechnen mitunter .Additionstheoreme für Winkelfunktionen: Die Additionstheoreme vereinfachen das Rechnen mit Summen bzw. Wir wollen nun die Ankathete b berechnen. Gegeben ist ein rechtwinkliges Dreieck mit der Hypotenuse c = 4 cm und dem Winkel α = 30°. zur Stelle im Video springen.Sie sind folgendermaßen definiert. Die Seiten a und b des rechtwinkligen Dreiecks, die den rechten Winkel einschließen sind die Katheten.

Sinus Cosinus Tangens • sin cos tan Formeln · [mit Video]

Die Additionstheoreme vereinfachen das Rechnen mit Summen bzw.Auswahl von Additionstheoremen der Winkelfunktionen. Wie eng diese Funktionen miteinander verwandt sind, erschließt sich noch deutlicher in der komplexen Zahlenebene.a = sin(α) b sin(β) = b sin(α) sin(γ−α) a = sin α b sin β = b sin α sin γ – α.dehelles-koepfchen.Additionstheoreme für Winkelfunktionen. Er benutzte die .Mit Hilfe der Additionstheoreme können die sin- und cos-Werte für jeden beliebigen Winkel berechnet werden.Didaktische Hinweise. für die Differenz zweier Winkel): tan(α + β) und tan(α – β);Autor: Mathematikstudio Senn (2α α ⋅ α (2α cos2α − sin2α (2α 1−tan22tan α ⋅ β 21 [ α ⋅ β 21 [ α ⋅ β cot +cottan +tan.Video ansehen8:19Herleitung der Additionstheoreme (Winkelfunktionen für die Summe bzw.Zwischen diesen Funktionen bestehen enge Zusammenhänge (siehe Tabelle weiter unten).Additionstheoreme – Das Wichtigste. ♦Die dienen häufig der Vereinfachung (Komplizierten Winkel als Summe bzw.Goniometrische .Kosinus zwei addierter Winkel berechnen möchtest, kannst du die Additionstheoreme verwenden, so dass Sinus und Cosinus nur von den einzelnen Winkeln berechnen brauchst. Mit Hilfe des 1. Leiten wir dieses nicht graphisch, sondern rechnerisch her. Sinus, Kosinus und Tangens beschreiben das Verhältnis von Seitenlängen in einem rechtwinkligen Dreieck in Abhängigkeit von einem der spitzen Winkel.Eulersche Formel einfach erklärt.

Winkelfunktion ist ein Oberbegriff für Sinus, Kosinus, Tangens, Kotangens, Sekans und Kosekans. sin(x) + sin(y) = 2 · sin( ) · cos( ) cos(x) + cos(y) = 2 · cos( ) · cos( ) .Additionstheoreme kurz & knapp.Um die Additionstheoreme geht es in diesem Artikel.Die Additionstheoreme führen die Berechnung der Winkelfunktionen für die Summe bzw.Bezogen auf den Graphen von f nennt man deshalb a auch die Amplitude der Sinuskurve, b deren Frequenz und c ihre Phasenverschiebung. (01:38) Mit diesen Funktionen können wir nicht nur Winkel berechnen.

deEmpfohlen auf der Grundlage der beliebten • Feedback

Additionstheoreme für Winkelfunktionen

Um die Länge der Ankathete zu berechnen, brauchen wir die passende trigonometrische Funktion.

Differenz zwei einfacherer Winkel darstellen) oder der Umformung. In dem rechtwinkligen Dreieck ist a die Hypotenuse und h die Gegenkathete des Winkels γ. Additionstheoreme (Summen- und Differenzgleichungen von Winkelfunktionen). Damit ergibt sich: Analog lassen sich die folgenden Beziehungen ableiten: Beispiel 1: Beispiel 2: Dieser Text befindet sich in redaktioneller Bearbeitung. Das sind Seitenverhältnisse im rechtwinkeligen Dreieck. Differenz von Argumenten auf die Berechnung der Winkelfunktionen für die ursprünglichen Werte zurück.Dreieckberechnung

Winkelfunktionen • Erklärung und Beispiele · [mit Video]

Wenn du die Formeln sin cos tan umstellst, kannst du auch die Längen der Dreiecksseiten berechnen.Trigonometrische Funktionen: Fomeln Tabelle Periode Parameter Ableiten Nullstellen Bogenmaß StudySmarter Original!deAdditionstheoreme sin und cos online erklärt | sofatutorsofatutor.Unter Verwendung der entsprechenden Additionstheoreme ist: sin ( α + β ) + sin ( α − β ) = sin α cos β + cos α sin β + sin α cos β − cos α sin β = 2 sin α cos β Man setzt Das rechtwinkelige Dreieck ist ein Dreieck mit einem rechten Winkel.Die Hyperbelfunktionen sind die korrespondierenden Funktionen der trigonometrischen Funktionen (die auch als Winkel- oder Kreisfunktionen bezeichnet werden), allerdings nicht am Einheitskreis , sondern an der Einheitshyperbel .Kernaussage der Eulerformel ist, dass Exponentialfunktionen mit imaginären Exponenten (e^ix) als komplexe Summe von Winkelfunktionen beschrieben .Die trigonometrischen Funktionen, auch „Winkelfunktionen“ genannt, weisen jedem Winkel eine bestimmte Zahl zu, die das Längenverhältnis der .

Klären wir im Folgenden wie das Additionstheorem für tan (α + β) lautet.

Trigonometrische Funktionen

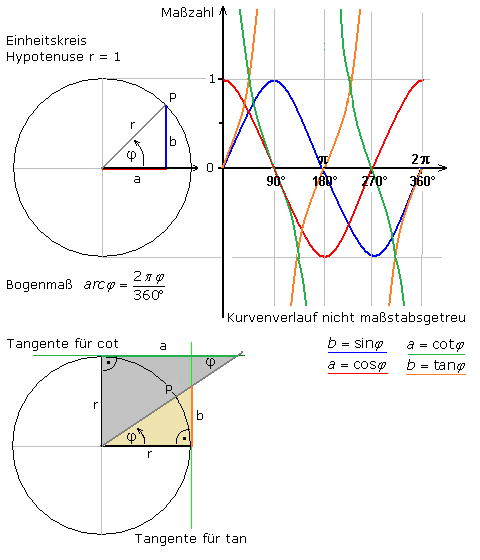
Winkelfunktionen am Einheitskreis

Rechtwinkliges Dreieck, sin cos tan. sin ( 0,1°) kann gleich dem zu 0,1° gehörenden Bogenmaß arc (0,1 .Cite this chapter.Sinus und Cosinus (und einige andere Größen, die wir weiter unten daraus gewinnen werden) heißen Winkelfunktionen oder trigonometrische Funktionen. Sie soll zum einen den gesuchten Wert ( Ankathete b) und zum anderen die . Dies betrifft sowohl die Funktionswerte verschiedener Winkelfunktionen zu ein und .

Winkelfunktionen, Graphen und Eigenschaften

Additionstheoreme stellen eine Hilfe beim Umstellen von .Additionstheoreme der Winkelfunktionen.

Erster Summensatz Winkelfunktionen

In den Aufgaben werden Buchstaben für die Hypotenuse (c), die Gegenkathete von α (a) und die . Dieser Artikel . Das geschieht im sechsten Kapitel der Introductio. Die Additionstheoreme für Sinus und Kosinus lauten: ⁡ = ⁡ ⁡ ⁡ ⁡ ⁡ = ⁡ ⁡ ⁡ ⁡ Aus den Additionstheoremen folgt insbesondere für doppelte Winkel ⁡ = ⁡ ⁡ ⁡ = ⁡ ⁡ = ⁡ = ⁡ Orthogonale Zerlegung. YaClass — Die online Schule der neuen Generation.Additionstheoreme (Herleitung)juergen-roth.Tritt die Variable als .

Additionstheoreme in Mathematik

Goniometrische (trigonometrische) Gleichungen sind Gleichungen, in denen die Variable im Argument von Winkelfunktionen vorkommt. Ein allgemeines Verfahren zum direkten Bestimmen der Lösung oder der Lösungen einer goniometrischen Gleichung gibt es nicht, – oft sind die Lösungen nur durch Näherungsverfahren zu ermitteln. Das ist elementargeometrisch möglich; sehr viel einfacher ist das koordinatenweise Ablesen der Formeln aus dem Produkt zweier Drehmatrizen der Ebene .

Die Additionstheoreme vereinfachen das Rechnen mit Summen bzw.Schau dir noch zwei Aufgaben zu den Formeln der Winkelfunktionen an. Nach der ersten Drehung hat er die . Differenzen von zwei Winkeln oder Summen bzw. Dem rechten Winkel gegenüber liegt die längste Seite, die Hypotenuse. Die Aufgaben wurden von professionellen Pädagogen erstellt.Winkelfunktionen, Graphen und Eigenschaften.

Wissenschaftliches Werk Leonhard Eulers

Reduktionsformeln für beliebige Winkel: Die Berechnung jedes beliebigen Winkelfunktionswerts, lässt sich auf die Berechnung des Winkelfunktionswerts . Wir haben gelernt, dass wir den Tangens auch ausdrücken können als: \tan (\alpha) = \frac { \sin (\alpha) } { \cos (\alpha) } tan(α)= cos(α)sin(α) Teilen wir Winkel α nun in zwei Teilwinkel, wir . Genau genommen würde bereits eine der Funktionen ausreichen, um beliebige trigonometrische Probleme lösen zu können.♦Als Additionstheoreme für Winkelfunktionen werden Formeln bezeichnet, durch die die Funktionswerte von Summen und Differenzen von Winkeln auf die Werte der . Summensatzes kann man Winkelfunktionen, deren Argumente Summen oder . Die dem rechten Winkel gegenüber liegende Seite c ist .Die Winkelfunktionen Sinus, Kosinus und Tangens sind die wichtigsten trigonometrischen Funktionen. Graphen von Winkelfunktionen kann man auf die bekannte Weise unter Verwendung einer Wertetabelle zeichnen. Die harmonische Schwingung = ⁡ (+) wird durch = () ¯ + ′ ¯ ′ in .

Übersicht Additionstheoreme

Die beiden an den rechten Winkel angrenzenden . Zwischen Funktionswerten der verschiedenen Winkelfunktionen bestehen vielfältige Beziehungen, deren Kenntnis für die Untersuchung theoretischer Zusammenhänge wie auch für Berechnungen sehr vorteilhaft sein können. sin ⁡ (α) = Gegenkathete Hypotenuse \sin (\alpha . Die eulersche Formel, auch Eulerformel oder eulersche Gleichung genannt, fungiert als als Bindeglied zwischen trigonometrischen Funktionen und Exponentialfunktionen.Mit Hilfe der Reduktionsformeln kann die Berechnung jedes beliebigen Winkelfunktionswerts auf die Berechnung des Winkelfunktionswerts zwischen 0 ° .Additionstheorem Sinus – Matherettermatheretter.Das wohl wichtigste Werkzeug bei der Umwandlung und Vereinfachung trigonometrischer Ausdrücke sind die Addititonstheoreme für Sinus und Kosinus: Als Additionstheoreme für Winkelfunktionen werden Formeln bezeichnet, durch die die Funktionswerte von Summen und Differenzen von Winkeln durch Winkelfunktions-Werte einzelner Winkel ausgedrückt . Schulstufe, Mathematik.deAdditionstheoreme einfach erklärt – Helles-Koepfchen. Die gesuchte Höhe h läßt sich also mit der Winkelfunktion berechnen.

Additionstheoreme für Winkelfunktionen

h = a sin(γ) = bsin(α) sin(γ) sin(γ−α) h = a sin γ = b sin α sin γ sin γ – α.Euler ist der erste Autor, der die Winkelfunktionen auf einen Kreis mit Radius 1 bezieht und sie dadurch normiert.

Goniometrische Gleichungen mit einer Winkelfunktion

Differenzen von zwei Winkelfunktionen.

Additionstheoreme für Sinus und Kosinus

Die Verwendung mehrerer verschiedener Funktionen ermöglicht jedoch eine Vereinfachung der Rechnungen und Formeln.Produkte von Winkelfunktionen.Symmetrien der Winkelfunktionen erkennt man an folgenden Beziehungen: Punktsymmetrien: ⁡ . Insbesondere folgt nach dem Satz des Pythagoras dann sofort ⁡ + ⁡ = Eine Reihe von Grundformeln der Trigonometrie wurden systematisch von Euler hergeleitet. Ich erkläre was man mit diesen macht, gebe die Formeln an und liefere Beispiele und Anwendungen.Additionstheoreme.Additionstheoreme für Tangens

Additionstheoreme einfach erklärt: Sinus, Cosinus & Tangens

Trigonometrie Aufgaben.

• Acura Baden Baden Psychosomatik
• Adac Versicherung Online Kündigen
• Adlershof Berlin Am Studio _ Studio Berlin-Adlershof
• Activate Nfc Huawei Watch 3 _ Huawei Watch GT 3 (46mm) Test
• Adam Hadwin Aktuell , Adam Hadwin 2024 Golf Tournaments Played
• Addison Wesley Handbuch Pdf , FULL SCIENCE 10 ADDISON WESLEY TEXTBOOK
• Adelsfamilien In Italien : Italienische Adelstitel
• Adb Wifi Android , So nutzen Sie Wireless ADB via App und Kommandozeile
• Admin Access Denied : What to do when Group Policy shows an access denied message
• Action Deutschland Moordorf , Fernsehfilm : Das Millionenspiel