Basislösung Simplex Tableau , Primales Simplexverfahren: Anfangstableau aufstellen
Di: Luke
Simplextableau aufstellen, Simplex-Algorithmus/-Verfahren
Dualer Simplexalgorithmus
02 – YouTubeyoutube.Simplex Tableau.
Interpretation Simplex-Tableau
Bei dem primalen Simplexverfahren (nur mit zulässiger Basislösung anwendbar) kann aus einer gegebenen zulässigen Basislösung eine optimale Basislösung gewonnen werden, wenn in der Zielfunktionszeile noch negative Werte gegeben sind. Ich erkläre euch an . Im Gegensatz zum primalen Simplexverfahren beginnt das duale Simplexverfahren . Durch Überführung auf Standardform.
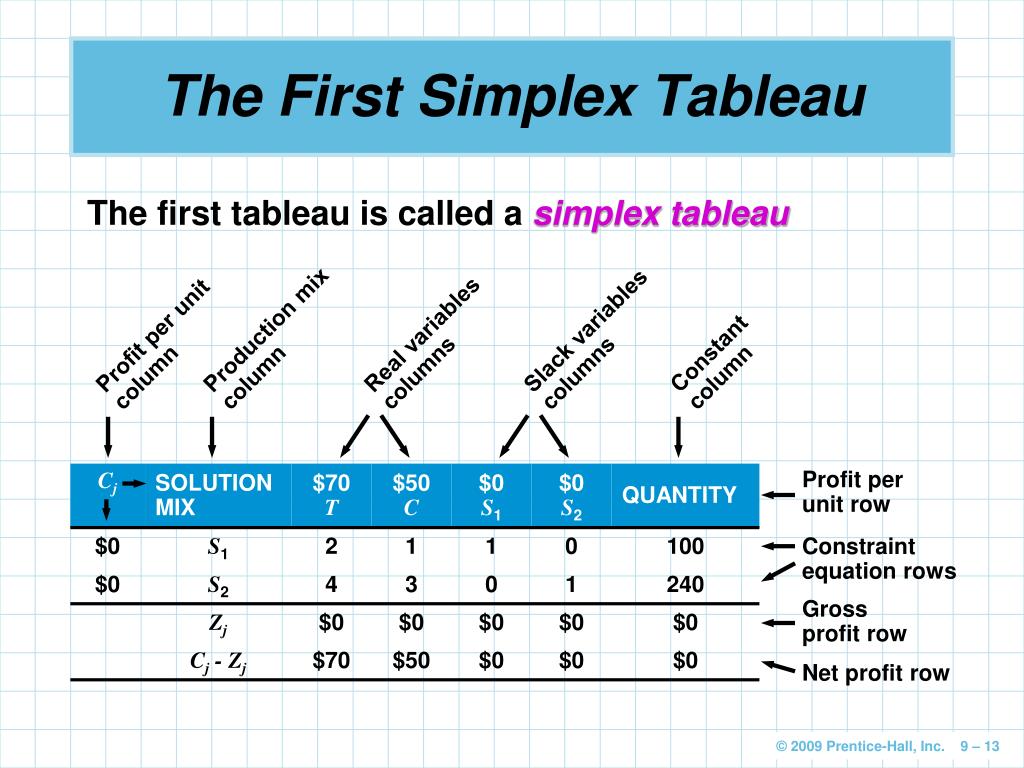
Teilt man die Zeilen I und II der Ergebnisspalte (ganz rechte Spalte) durch die jeweiligen Werte der Pivotspalte, ergibt das 3:1 = 3 für . Suche den minimalen negativen Wert in z-Zeile ⇒ Pivotspalte 9. Download reference work entry PDF.2 Simplex-Tableau Als nächstes werden die Gleichungen nun in ein so genanntes Simplex-Tableau überführt. Erfahren Sie, wie Sie eine Verbindung zu Daten herstellen, Datenvisualisierungen erstellen, Ihre Erkenntnisse .Schritt 3: Simplex-Tableau mehrmals umformen Pivotelement bestimmen.
Wann ist ein Simplex Tableau optimal?
Es löst ein solches Problem nach endlich vielen Schritten exakt oder stellt dessen Unlösbarkeit oder Unbeschränktheit fest. Das bedeutet, es kann eine beliebige Spalte als Pivotspalte gewählt werden. x 1 =10 +12·x 2 – x 3. A schematic, numerical representation that displays the transformed data set associated with a basic solution to a linear-programming problem. Das heißt es gibt keine Nebenbedingung, die x 2 einschränkt. Gibt es dort keine negativen Werte der Variablen, ist die aktuelle Basislösung optimal und das Simplex Verfahren ist beendet. Polynomielle Laufzeitkannnicht nachgewiesenwerden, aber in Das Tableau wird aktualisiert, indem man die Zeile mit Index durch dividiert, und für jedes von der Zeile mit Index die modifizierte Zeile mit Index , multipliziert mit , subtrahiert.
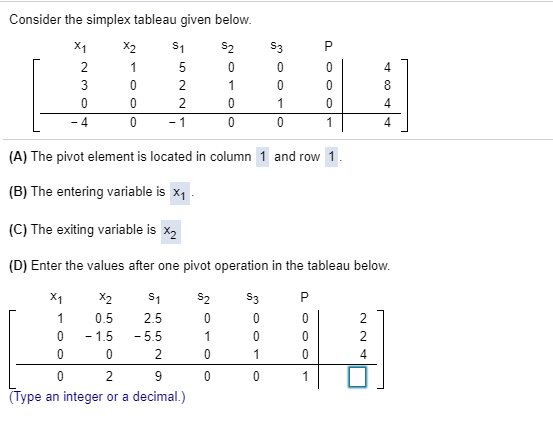
Daraus ergibt sich das folgende Optimaltableau: Tab.
Simplextableau Umformung für Dummies
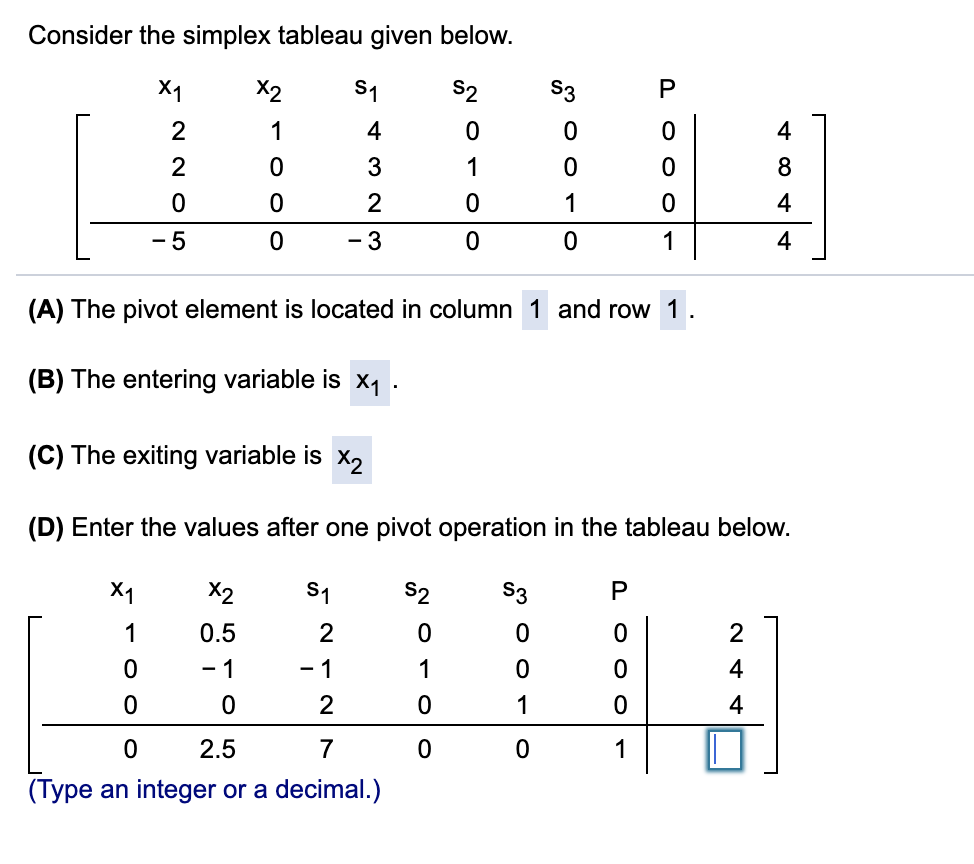
Um das Simplex-Verfahren besser zu verstehen, ist es hilfreich, einen detaillierten Blick auf die beiden Phasen zu werfen:1. Dantzig [1951].
Unzulässige und Zulässige Lösungen von LPS
Simplextableau aufstellen, Simplex-Algorithmus/ . Die Normalform wird dadurch hergestellt, dass die Ungleichungen durch das Hinzufügen einer sogenannten Schlupfvariable in .
Simplex Tableau verstehen
Auf der linken .Tableaus: 1·x 1-2·x 2 + x 3 =60 Aufgelöst nach x 1.Anfangs-Simplex-Tableau: Die (zulässige) Basislösung ist. Berechnet ein Simplex-Ta bleau bis zu 18 Spalten und 10 Zeilen. Das folgende Schema erhält man, wenn lediglich die Vorfaktoren der Gleichungen und . Download chapter PDF. als letzte Zeile hinzufügen.
simplex me
Bevor der Simplexalgorithmus zum Einsatz kommen kann, muss das Problem in ein Tableau eingetragen werden. Das optimale Endtableau ist gegeben mit: x 1 = 5 2, x 2 = 3 4 . Wenn wir in diesem Tableau und setzen, dann können wir die Variablen , , und sofort aus dem Tableau .
comEmpfohlen auf der Grundlage der beliebten • Feedback
Simplex-Verfahren
Sprachlinks befinden sich oben auf der Seite gegenüber dem Titel. Ungleichungen beschreiben die .Das unzulässige Tableau kann des Weiteren mit dem dualen Simplex-Algorithmus überarbeitet werden: Die x 2 -Zeile als Pivotzeile ist die betragsmäßig größte und einzige negative Zahl. (Das ist meist eine Basislösung mit ,d. In dem obigen Beispiel sind beide Werte gleich (-1). 246K views 10 years ago Lineare Optimierung, Simplex-Verfahren, Operations Research.Herstellen der Normalform. xDie Variablen in der . In jeder Zeile ist eine der Gleichungen enthalten.Zunächst wählen wir wieder Pivotzeile und -spalte aus: Dualer Simplex – Auswahl Pivotzeile und -spalte.Nachdem das Tableau für das lineare Optimierungsproblem im vorherigen Abschnitt aufgestellt worden ist, soll nun die erste Iteration für das duale Simplexverfahren durchgeführt werden. Schritt: Wahl der Pivotspalte. Die sogenannte Pivotspalte ist die Spalte, bei welcher der Zielfunktionskoeffizient (in der untersten Zeile) am geringsten ist; das ist mit -3 die t-Spalte.dürfen, existiert bereits zu Beginn eine zulässige Basislösung: x = (0,0,2400,10,20) Anwendung des Simplex-Algorithmus‘ Wir tragen nun das lineare Optimierungsproblem (Normalform) in das Tableau ein.Zu jeder Basislösung gehört eine entsprechende Struktur der Nebenbedingungen ABxB +ANxN = b mit x ¯B = A −1 B b, x¯N = 0 (1) und der Zielfunktion: Q(xB,xN) = c T BxB +c T NxN. Es wird diejenige Spalte als Pivotspalte ausgewählt, für welche der Zielfunktionswert den kleinsten negativen Wert annimmt. Hinweis zum Ablesen der Lösung.Das Simplextableau.Berechnet ein Simplex- Tableau bis zu 10 Spalten und 6 Zeilen. Tableau I BASIS x 1 x 2 x 3 x 4 x 5 RHS Ratio .Das Simplex-Tableau stellt eine verkürzte Schreibweise des Gleichungssystems dar. In diesem Fall ist nun die erste Spalte gewählt worden.Ein Simplex-Verfahren (auch Simplex-Algorithmus) ist ein Optimierungsverfahren der Numerik zur Lösung linearer Optimierungsprobleme, auch als Lineare Programme (LP) . die Basislösung hat sich nicht . Wir schreiben das lineare Gleichungssystem in Matrixform an, wobei wir auch als Variable auffassen und die Zielfunktion, in Form der Gleichung.The Simplex Tableau • xN determines xB as xB +B −1Nx N = B −1b • Plus we know that z = cB TB−1b+(c N T −c B TB−1N)x N z +0xB +(cB TB−1N−cN T)xN = cB TB−1b • In the .Das Simplex Verfahren ist eine mathematische Methode zur Lösung linearer Optimierungsprobleme bzw. The pivot row and column are indicated by arrows; the pivot element is bolded. zur Feststellung der Nichtexistenz einer optimalen Lösung. Überprüfung der Zulässigkeit der Basislösung.Bestimmung einer Basislösung. Dieses ist wie folgt aufgebaut: Erläuterung des Tableaus zu Beginn des Verfahrens. Die wichtigsten Verbesserungen, die heute zum Standard in guten LP-Lösern gehören, sollen hier .
Simplexalgorithmus: Herstellen der Normalform
Der einfachste Fall liegt vor, wenn das Ausgangsproblem die Form. Reference work entry. Dagegen wird von den Nichtbasisvariablen im jeweiligen Schritt eine null angenommen.Simplex Tableau, Zielfunktion und Nebenbedingungen aus Text herauslesen. Simplex Algorithmus In diesem Video geht es um den Simplex Algorithmus. Initialisierungsphase: Erstellung des Anfangs-Simplex-Tableaus.
The Simplex Tableau
Diesen Termen wird im jeweiligen Simplex-Tableau keine null zugewiesen.Sichere dir jetzt die perfekte Prüfungsvorbereitung! In diesem Online-Kurs zum Thema Weiterer Simplex-Schritt und Interpretation des Optimaltableaus wird dir in anschaulichen Lernvideos, leicht verständlichen Lerntexten, interaktiven Übungsaufgaben und druckbaren Abbildungen das umfassende Wissen vermittelt. Zeile eingetragen, die . Ich habe eine Aufgabe, bei der man die Zielfunktion und die Nebenbedingungen zum Aufstellen . (2) Das lineare Programm lässt sich dann äquivalent so umformen, dass in den Nebenbedingungen vor den Basisvariablen die Einheitsmatrix steht und in der . Cite this reference work entry.comÜbungen – Aufgaben + Lösungen Simplexalgorithmus – . Bilde die Quotienten zwischen bi-Spalte und Pivotspalte abiji für alle positiven aij und wähle den minimalen Quotienten ⇒ . Simplextableau aufstellen, Simplex-Algorithmus/-Verfahren Wenn noch . Bedingungen: a 11 x 1 + a 12 x 2 + a 13 x 3 ≤ b 1.
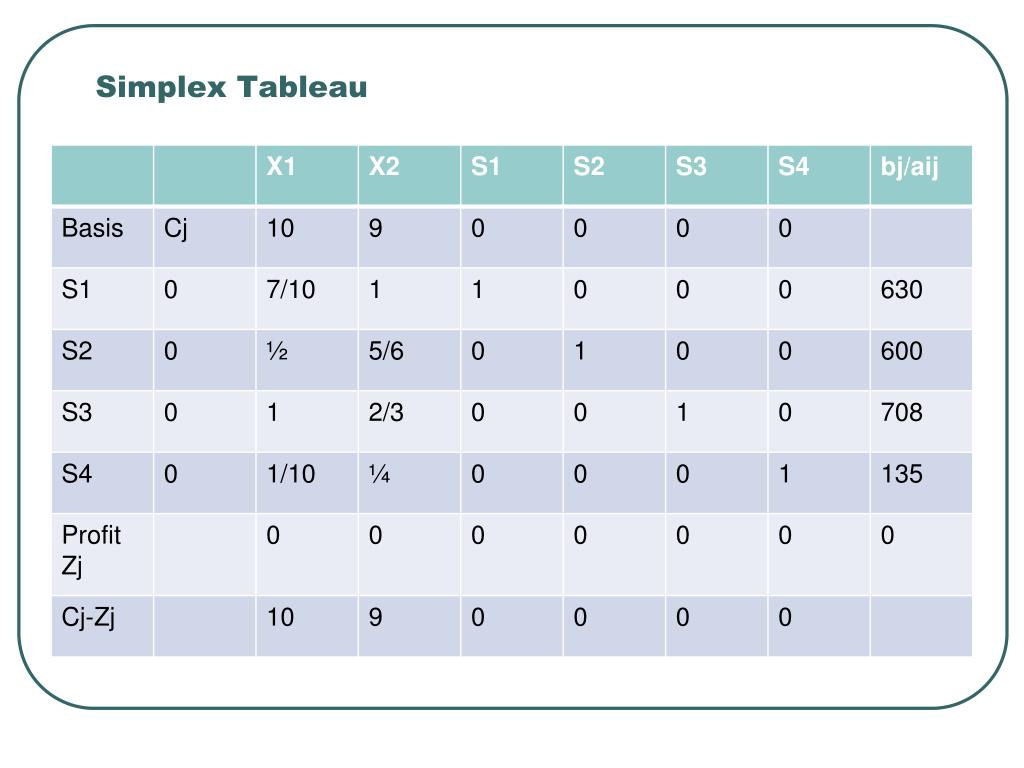
Jede Variable erhält .comSimplex-Algorithmus, Beispiel 1 | M. Nach dem ersten Pivotschritt erhalten wir: mit der Basislösung. Entwickelt vonG.
Primales Simplexverfahren: Anfangstableau aufstellen
Dazu wiederum muss das Problem in die sogenannte Normalform gebracht werden. Meist habt ihr dann eine Zielfunktion und Bedingungen wie folgt gegeben: Zielfunktion: z=c 1 x 1 +c 2 x 2 +c 3 x 3 +d.Ja → optimale Basislösung gefunden → Lösung aus Optimaltableau ablesen Nein → optimale Basislösung noch nicht gefunden → Primalen Simplex anwenden 8. Da in allen Zeilen negative Koeffizienten in der Pivotspalte sind, ist entsprechendes dort der Fall.Das bekannteste analytische Lösungsverfahren der linearen Optimierung ist die Simplex-Methode., pick the variable with the most negative coe cient to enter the basis.1 Ungleichungen.comEmpfohlen auf der Grundlage der beliebten • Feedback
SIMPLEX Algorithmus
First Online: 01 January 2016. 6: Optimaltableau. Bislang blieb offen, wie man eine zulässige Basislösung zum Start des Simplex-Verfahrens erhält. We use the greedy rule for selecting the entering variable, i. Diese Ausgangstabelle wird als Basislösung bezeichnet.Das Simplex-Verfahren (auch Simplex-Algorithmus) ist ein Optimierungsverfahren der Numerik zur Lösung linearer Optimierungsprobleme.
Webinar: Operations Research Thema: Simplex-Algorithmus
Bei dieser Lösung sind x 1 und x 2 gleich 0 und es würde nichts produziert werden. 84K views 3 years ago BWL / VWL. Danach wenden wir den Simplexalgorithmus an und gelangen zum Endtableau: Dualer Simplex – Endtableau. Nach zwei Pivotschritten erhalten wir: Im Tableau ist aber nur mehr ein (statt zwei) Koeffizienten in der ZFZ ungleich Null. Lösen des lineare Optimierungsproblem ( Abbildung ). x 1 x 2 b i x 3 200 100 2400 x 4 1 0 10 x 5 0,5 1 20 ZF -350 -260 0 Die Nichtbasisvariablen werden in die 1.SIMPLEX Algorithmus – lineare Optimierung, Tableau : r . \Excel 97\LPG 2.Unendlich viele Lösungen.Das Simplexverfahren findet in einem sogenannten Simplex-Tableau statt. Hier wird der kleinste negative Wert ausgewählt um die Pivotspalte .Es ergibt sich folgendes Tableau: Das Ergebnis lautet: z=960; x 1 =160; x 2 =0; x 3 =-48; x 4 =0; x 5 =-9. Wir können daher das Standardverfahren verwenden.
Der Simplex-Algorithmus
Simplex Tableau verstehen im Mathe-Forum für Schüler und Studenten Antworten nach dem Prinzip Hilfe zur Selbsthilfe Jetzt Deine Frage im Forum stellen! Mathe . Diese befindet sich nicht am linken, sondern nur am oberen Rand. For the problem: Minimize cx, subject to Ax = b, x ≥ 0, if the m × m matrix B is a feasible basis and the m × 1 row vector c0 the ordered cost coefficients for the variables in the . 535K subscribers. Die Grundidee des Simplex-Verfahrens wurde 1947 von George Dantzig vorgestellt.Beim Simplex-Algorithmus geht man anfangs immer von einer Basislösung aus.
Das Simplextableau
Es sind keine negativen Werte mehr auf der rechten Seite gegeben. Erhöht man x 2 wird auch x 1 größer. Beispiel: Beispiel: Simplex-Algorithmus automatisch erstellt am 19. Das verkürzte Simplex-Tableau wird folgendermaßen interpretiert: Alle Nichtbasisvariablen (alle Variablen der Kopfzeile) . mit dem Simplex-Algorithmus: Die Basislösung ist zulässig.modifiziert eine zulässige Basislösung mit sukzessiven Pivot-Operationen, .In diesem Artikel. Diese Basis-Lösung ist immer zulässig. findet man sofort die Basislösung .Interpretation des gelösten Simplex-Tableaus: Um die Lösung des Optimums aus dem Simplex-Tableau ablesen zu können, müssen die Basisvariablen bestimmt werden. \Excel 97\LPG 3.The simplex method is performed step-by-step for this problem in the tableaus below. Dafür schaust du dir die F-Zeile an. Bei der Einrichtung einer Unternehmensumgebung, die sich skalieren lässt, um mit Ihrem . Es wird als erstes die Pivotspalte bestimmt.Die ordnungsgemäße Bereitstellung und die Planung der Skalierung sind entscheidende Faktoren, um Systemausfälle zu minimieren und sicherzustellen, dass Ihre Analyseplattform den ständig wachsenden Anforderungen Ihres Unternehmens gerecht werden kann.Der Simplex-Algorithmus, oder auch Simplexverfahren genannt, ist eine Möglichkeit lineare Ungleichungen zu lösen und dessen Maximum anzugeben.
Unendlich viele Lösungen
Zu transformieren sind die Gleichungen in ein sogenanntes Simplex-Ausgangs Tableau. Zu verstehen sind die Zahlen der. Ein wichtiges Beispiel für den angegebenen Fall hat man mit .In diesem Video zeige ich euch, wie ihr die Tabelle für das Simplex Verfahren aufstellt und wie der Ablauf/Algorithmus funktioniert um zur Lösung des Optimie. In der zeichnerischen Darstellung ist zu erkennen, dass der Lösungsbereich in Richtung . Diese Ausgangslösung wird am . Für jede Iteration müssen die folgenden Schritte durchgeführt werden. Das bedeutet genau, dass x1, x2 vorerst Nichtbasisvariablen sind, d.Ausgehend von einer Basislösung geht man von Eckpunkt zu Eckpunkt des zulässigen Lösungsraums und schaut, ob damit schon die optimale Lösung gefunden ist. Basisvariablen (= Werte der rechten Seite) Nichtbasisvariablen (= .Der Simplex-Algorithmus Erste Algorithmuszur Lösung allgemeiner linearer Programme.Der Simplex-Algorithmus zur Lösung eines linearen Programms modifiziert eine zulässige Basislösung mit sukzessiven Pivot-Operationen, bis ein optimaler Vektor erreicht ist. Wir erhalten dadurch das Anfangs-Simplex-Tableau. Tutorial: Erste Schritte in Tableau Desktop. Es fällt auf, manche Variablen haben negative Werte, die Nichtnegativitätsbedingungen sind teilweise verletzt und die Basislösung ist keine zulässige Lösung des Linearen Optimierungsproblems .Liegen die Nebenbedingungen in Gleichungsform vor, können alle Koeffizienten des Problems in ein sogenanntes Simplex-Tableau übertragen werden.Ein Standard-Maximierungsproblem liegt vor, wenn die Basislösung des Anfangs-Simplex-Tableaus zulässig ist.Im Laufe der Zeit sind einige Varianten des Simplex-Verfahrens entwickelt worden, die die Rechenzeit und den Speicherbedarf beim Lösen linearer Programme gegenüber dem Standardverfahren deutlich verkürzen und numerisch deutlich stabiler sind. Weil -2 die einzig negative Zahl in der Pivotzeile ist, lautete der zu betrachtende Quotient: –1/(–2) = 0,5.Wann endet der Simplex Algorithmus? Erster Iterationsschritt: Wahl der Pivotspalte Daher wird der Algorithmus auch häufig als Pivotverfahren bezeichnet.
- Barkley Marathon 2024 Anmeldung
- Barmer Widerspruch Pflegegrad | Pflegestufe 3: Antrag und Widerspruch
- Barzahlung Auto Finanzieren | Barzahlen oder finanzieren: Was beim Autokauf besser ist
- Barrierefreies Bauen Leitfaden
- Barmherziger Gott Deutschland | Über die Barmherzigkeit Gottes
- Batterie Für Macbook Pro Kalibrieren
- Basketball Neuseeland Nationalmannschaft
- Barmer Quakenbrück Lange Str : Kreissparkasse Bersenbrück
- Basics Of Usb Audio , Fundamentals of USB-Audio
- Battlefield 4 Patch Notes _ Battlefield 2042 Update 4: Release Date, Patch Notes, Size
- Battlespire Download | The Elder Scrolls
- Bass Test Song – 25 of the best tracks for testing bass
- Basteln Zum Valentinstag Ideen
- Basalt Nuanciert – Beschreibung