Betragsfunktion Graph Beispiel
Di: Luke
Sie nimmt nur Werte aus dem Intervall [0,\infty] [0,∞] an.

Injektiv Surjektiv Bijektiv · Aufgaben & Beweise · [mit Video]
Ableitung der Betragsfunktion – die .Weitere Beispiele und Hintergründe zur Betragsfunktion an sich findest Du in der Erklärung Betragsfunktionen. Den Graphen der Funktion $y = |f(x)|$ erhält man aus dem Graphen von $y = f(x)$, indem man alle unterhalb der $x$-Achse liegenden Kurvenstücke an der $x$-Achse . f ( x) = { − 3 x, x ≤ 1 x − 2, x > 1. Stetigkeit: Definition Beweisen Differenzierbarkeit Unstetigkeit Funktionen .Aufgaben zur Betragsfunktion.Der Graph einer Funktion f (x) ist eine Zeichnung der Funktion in der Ebene. Du findest auf der Zahlengeraden links von der Null die negativen Zahlen und rechts von der Null die positiven Zahlen.
Betrags- und Signumsfunktion
Die Betragsfunktion y=|x| y = ∣x∣ ordnet jeder reellen Zahl ihren Absolutbetrag zu und ist für alle reelle Zahlen definiert.Die Betragsfunktion ist ein Beispiel für eine stückweise erklärte stetige Funktion. Gleichungen mit Absolutbetrag. An der Stelle x=0 x = 0 besitzt sie ein Minimum. Prüfe dein Wissen anschließend mit Arbeitsblättern und Übungen. (00:40) Um Funktionen zu untersuchen und ihre Eigenschaften zu verstehen, gibt es verschiedene Möglichkeiten und Grundlagen, die du kennen solltest.Zeichne Betragsfunktionen (Übung) | Khan Academy.Spezielle Funktionen: Betragsfunktion, Vorzeichenfunktion, Gaußsche Glockenkurve Zusammengesetzte Funktionen: beliebig Zu jeder Gruppe gehören verschiedene Typen von Funktionen. Funktionen können auch an der -Achse gespiegelt werden. Lernen mit Serlo
Graph einer Funktion • Erklärung, Beispiele · [mit Video]
Betragsfunktionen – Überblick. Schau dir Beispielaufgaben an, bei denen diese . Graph von y=|x+3|-2.Funktionen Grundlagen. ( | x |) = − 1.
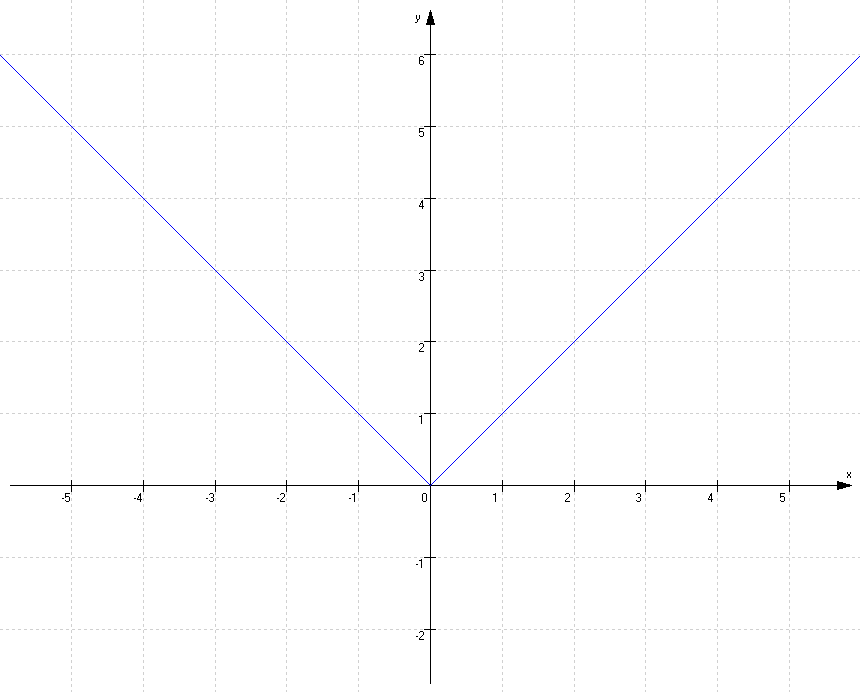
Lerne den Betrag → Hier lernst du die Definition, Rechenregeln, die Abschnittweise definierte Betragsfunktion, Auswirkungen auf den Zahlenstrahl, auf die Kurvendiskussion mit vielen Beispielen und Graphen erklärt.
Betragsfunktion in Mathematik
Beispielaufgabe 1. nicht differenzierbar ist. Dies ist gleichbedeutend dazu, dass der Hypograph der Funktion, also die Menge der Punkte unterhalb des Graphen, eine konvexe Menge ist. Beispiel Der Graph der Funktion ist im Vergleich zum Graph der Funktion an der -Achse gespiegelt. Man rechnet wie folgt: Die Gleichung besitzt also genau zwei Lösungen für , nämlich 2 und −8.
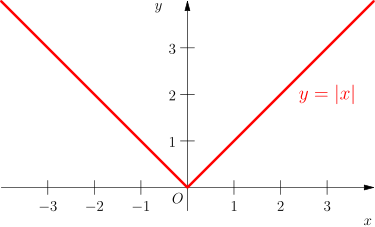
zur Stelle im Video springen.Betragsfunktionen graphisch darstellen – Einfach erklärt anhand von sofatutor-Videos. Es folgt für dich: Verschiebe Betragsfunktionen Schaffe 3 von 4 Aufgaben, um ein höheres Level zu erreichen! Starte. Wenn k<0, ist er auch gespiegelt (oder geklappt) an der x-Achse.Zwischen zwei Betragsstrichen können nicht nur Zahlen, sondern auch Teile eines Funktionsterms stehen. Sie werden daher auch „Polynomfunktionen“ genannt. Mit E-Mail registrieren. Graph von y=3|x|. (03:53) In diesem Beitrag und im Video erklären wir dir die Begriffe Injektivität, Surjektivität und Bijektivität. Die beiden Halbgeraden haben die Steigung +1 und -1.
Funktionen mit Tabellen und Graphen beschreiben
In dieser Beispielaufgabe, bestimmen . Absolutwertfunktionen zeichnen. Zuerst wollen wir mit der .
Betrag und Betragsfunktion jetzt unkompliziert lernen!
Anschließend wählst du soviele weitere Punkte aus dem Graphen, wie du weitere Parameter in der Funktionsgleichung hast und löst die entsprechenden Gleichungen nach diesen Parametern (hier b und c) auf. Das führt zum nebenstehenden Graphen. Nach den obigen Vorbetrachtungen .Zur Erinnerung: Betrag einer Zahl Zahlengerade . | − π | = π.Die Betragsfunktion hat ein paar Besonderheiten: Ihr Minimum ist bei x = 0 mit einem Funktionswert y = 0; dieser Tiefpunkt kann aber nicht wie üblich über das Gleichsetzen der 1.Grundlagen zum Thema Betragsfunktionen graphisch darstellen. Diese ganz-rationalen Funktionen nennt man auch Polynome oder Polynomfunktionen.Eine Wurzel kann als Exponent geschrieben werden; Ableitung mit der Kettenregel; Funktion vereinfachen. Nach dem Schauen dieses Videos wirst du in der Lage sein, Betragsfunktionen graphisch darzustellen. Die formale Definition des absoluten Betrages ( Absolutbetrag s) einer reellen Zahl x ist die . (02:38) Bijektiv. Verschiebung in $y$-Richtung. f: x ↦ | x | D = R W = R + 0. Funktionen mit Tabellen und Graphen beschreiben. Ist jedoch , dann ist . Verschiebung in $x$-Richtung. Wir erhalten für die Wertetabelle: Der zugehörige Funktionsgraph (in Grün) sieht dann so aus: Der Graph ist . Strecken und Stauchen in $y$-Richtung.Das Pluszeichen schreibst du meist gar nicht mit.
![Graph einer Funktion • Erklärung, Beispiele · [mit Video]](https://d1g9li960vagp7.cloudfront.net/wp-content/uploads/2022/10/Kurvendiskussion-1024x709.png)
Khan Academy ist eine Non-profit Organisation mit dem Zweck eine kostenlose, weltklasse Ausbildung für jeden Menschen auf der .Themen und Stichworte zu diesem Modul: Betragsfunktion – Betragsfunktionen – Betrag – Beträge – Betragsgleichung – Betragsgleichungen – Funktion – Funktionen mit Betrag – Absolutbetrag – Absoluter Betrag – Plotten – Grafisch – Graph – Bild – Grafik-Werte – Berechnung – Berechnen – Darstellen – Grafische Darstellung – Rechner – Rechnen mit . \mathrm {f} (\mathrm . Stelle g ( x) = − 5 | x + 2 | + 2 grafisch dar.Mit dem Zahlenstrahl kann man reelle Zahlen darstellen, indem man sie als Punkte auf diesem Zahlenstrahl markiert, zum . mathphys-online Abschnittsweise definierte Funktionen Stetigkeit und Differenzierbarkeit 3 1. Die Betragsfunktion f (x) = |x| ordnet der Zahl -5 die Zahl 5 zu; der Zahl 5 ordnet sie (ebenfalls) die Zahl 5 zu. Sie ordnet jedem x x -Wert seinen Betrag zu.Der Graph von y=|x-h|+k ist der Graph von y=|x| der um h Einheiten nach rechts und um k Einheiten nach oben verschoben ist.Betragsfunktion in Mathematik | Schülerlexikon | Lernhelferlernhelfer. Es gibt dabei im wesentlichen drei Ansätze: Man . Wie gut kennst du dich mit der Betragsfunktion aus? Vertiefe dein Wissen mit diesen gemischten Übungsaufgaben! 1. Zunächst lernst du, was die Eigenschaften von Beträgen und Betragsfunktionen sind.
Differenzierbarkeit von Funktionen in Mathematik
Im Folgenden soll dabei immer von einer reellwertigen Funktion einer Variablen die Rede sein. Ist der Vorfaktor negativ, wird die Funktion an . Der Funktionsterm der gestreckten Funktion sieht dann folgendermaßen aus: Die Graphen der beiden Funktionen sehen dann so aus: Streckung und Stauchung in x-Richtung. f(x) = | x | ≥ 0. Wir sollen zeichnen: f ( x) = | x − 1 | + 5.Beispiel: 1 Ein „klassisches“ Beispiel ist die Betragsfunktion f (x) = | x |, die an der Stelle x 0 = 0 stetig (sie ist überall in ℝ stetig), aber nicht differenzierbar ist.Die Betragsfunktion ist an der Stelle x=0 x = 0 nicht differenzierbar. Die einfachste Betragsfunktion ist f (x)=\vert x \vert f (x) = ∣x∣. | – 1 2| = 1 2. Für eine Veränderung des Graphen in -Richtung multipliziert man das Funktionsargument mit . Bearbeite 4 Aufgaben.Beispiel: | – 2,5| = | + 2,5| = 2,5.Einige Beispiele: Graph von y=|x|. Ableitung bei 0 nicht existiert (nicht differenzierbar an der Stelle); Die 1.Eine wichtige Aufgabe bei solchen gegebenen Funktionen ist, eine Vorstellung von deren Graphen zu bekommen. Die Nicht-Differenzierbarkeit bei 0 ist anschaulich klar: Der Graph ändert im Punkt ( 0 ; 0 ) plötzlich seine Richtung, und es gibt keine Tangente. Es folgt für dich: Verschiebe Betragsfunktionen . Der Definitionsbereich der Funktion f ( x) ist D f . Dabei wird in die Begriffe Funktion, Funktionsgleichung und Funktionsgraph unterschieden. Ist jedoch , dann . lernst du in der 9. Hier bietet sich zum Beispiel g(0) = 0 an (und noch ein weiterer). Negative Zahlen werden somit zu gleichhohen positiven . Google Classroom. Dabei benutzt man die abschnittsweise Definition des Betrags . Transformierte Betragsfunktionen.
Die Betragsfunktion untersuchen
Die Signumsfunktion y=\sgn x y = sgnx ordnet jeder Zahl ihr Signum .für den rechtsseitigen Grenzwert geht man von oben gegen x 0 , setzt also x-Werte ein, die immer ein bisschen größer als x 0 sind. Trägst du alle Punkte einer Funktion in ein Koordinatensystem ein, kannst du sie so graphisch darstellen. Abhängigkeit einer Größe von einer anderen Größe. Ein Graph kann zum Beispiel so aussehen: Graph einer Parabel. Übungen – sofatutor. Aus folgt für reelle Zahlen oder .Betragsfunktionen graphisch darstellen. für , da für Werte der Term negativ ist.
Betrags- und partielle Funktionen
Beispiel: Wir möchten den Graphen der Funktion um den Faktor in -Richtung strecken.In dieser Abbildung ist der Graph einer ganz-rationalen Funktion dargestellt.
Besondere lineare Funktionen: Beschreiben & Beispiele
Betrag und Betragsfunktion jetzt unkompliziert lernen! | a | = { a, wenn a ≥ 0 − a, wenn a < 0. 1 2 3 4 5 6 7 − 2 − 3 − 4 − 5 − 6 − 7 1 2 3 4 5 6 7 − 2 − 3 − 4 − . Begründe, weshalb die Funktion f ( x) mit.Differenzierbarkeit Beispiele und Aufgaben. , da der Term für alle Werte von x negativ ist. Sie ist wegen |x|=|-x| ∣x∣ = ∣ − x∣ eine gerade Funktion. Graph von y=-|x|.Der Differentialquotient ist also der Grenzwert des Differenzenquotienten für ein immer kleiner werdendes Intervall. Folgende Zahlenbeispiele zeigen die Funktionsweise der Betragsfunktion.Absolutwertfunktionen zeichnen.Der Graph von y=k|x| ist der Graph von y=|x| mit dem Faktor|k| gestreckt. Die Zahlen haben verschiedene Vorzeichen: minus und plus. Graph der Funktion . Ableitung mit 0 gefunden werden, da die 1. ( Beispiel 166A) Signumsfunktion. Der Nenner der vereinfachten Funktion entspricht dabei der Definition der Betragsfunktion.deDie Standardform einer Betragsfunktion ist f(x)= |x|.
Betragsfunktion
Lerne kostenlos Mathe, Kunst, Informatik, Wirtschaft, Physik, Chemie, Biologie, Medizin, Finanzwesen, Geschichte und vieles mehr.Dann wählst du a so, dass der Knick dem im Graph entspricht. Willst du den Graphen einer Funktion selber zeichnen, kannst du dafür eine Wertetabelle benutzen.Motivation [Bearbeiten].Graph der Betragsfunktion x-Achse y-Achse Anschaulich bedeutet dies, dass der negative Teil der Argumentfunktion y = x (gestrichelt) an der x-Achse gespiegelt wird. Skaliere & spiegle Betragsfunktionen Schaffe 3 von 4 Aufgaben, um ein höheres Level . Nicht begonnen.3 Zusammengesetzte lineare Betragsfunktionen Bei zusammengesetzten . Polynomfunktionen (Ganzrationale Funktionen) Diese Funktionen ergeben sich aus Polynomen. Anschließend lernst du, wie du den Graphen einer Betragsfunktion in einem . Es gibt dabei im wesentlichen drei Ansätze: Man kann .
Komplexe Zahlen: Darstellung komplexwertiger Funktionen
![]()

Sie ist immer achsensymmetrisch.Betragsfunktion und Signum-Funktion Wie weit eine Zahl auf dem Zahlenstrahl von der Null entfernt ist, . Die genaue Polynomfunktion des Graphen lautet f (x) = 3 x 3-5 x 2 + 4. Einer der ersten, der sich mit den Eigenschaften .Kurven in ParameterdarstellungDie Wurzelfunktion Untersuchen
Betragsfunktion
deBetragsfunktionen erklärt inkl.Betragsfunktionen skalieren & spiegeln: Graph. Als Beispiel sind alle Zahlen gesucht, welche die Gleichung erfüllen. Inhaltsübersicht. Vorzeichen – Betrag.Die Ableitung gibt die Steigung des Graphen der Betragsfunktion an.Was genau ein Polynom ist, welche speziellen Eigenschaften es hat und wie Du es richtig berechnest, erfährst Du in . Dabei schauen wir uns wichtige Eigenschaften an und zeigen viele Beispielaufgaben mit Lösungen.Kostet nichts – Hilft Dir bei allen Themen: http://www. Eine Funktion drückt immer den Zusammenhang . Graphen von Funktionen mit Beträgen.
Funktionen
Allgemein gilt: |a| = { a für a ≥ 0 – a für a < 0.Der Graph der Betragsfunktion. Die lineare Betragsfunktion y = |x|. Dann entsteht eine neue Funktion. Ein Problem melden. Tangente, Sekante und Passante Unter den Begriffen Tangente , Sekante und Passante werden in der Mathematik Geraden verstanden, welche eine Funktion oder geometrische Figur berühren, schneiden oder nicht berühren. Sie ist für x\leq 0 x≤0 monoton .Eine reellwertige Funktion heißt konkav (lateinisch: concavus = gewölbt), wenn ihr Graph oberhalb jeder Verbindungsstrecke zweier seiner Punkte liegt. Wenn wir eine Funktion : untersuchen wollen, ist es hilfreich, sich einen Funktionsgraphen aufzuzeichnen.
Wie skizziert man Betragsfunktionen? (mit 4 Beispielen
In diesem Video stellen wir dir anhand von 4 Beispielen vor, wie man Betragsfunktionen skizzieren kann. Wenn du alle Zahlen nimmst und den Zahlen . Für viele Anwendungen innerhalb der Mathematik und in der Praxis ist es wichtig, das Änderungsverhalten einer Funktion zu beschreiben. Wende nun Dein gelerntes Wissen an zwei Beispielen an. Betrachten wir beispielsweise die Funktion :, ():=. Die -Achse ist ein Zahlenstrahl.chEmpfohlen basierend auf dem, was zu diesem Thema beliebt ist • Feedback
Betragsfunktionen
- Betriebsleiter Landwirtschaft Genehmigung
- Better Sax Burnin Alto Saxophone
- Betriebsausgabenpauschale Forst
- Beton Druckfestigkeitsentwicklung
- Betonestrich Preisliste – GO/ON! Beton-Estrich grau 30 kg
- Bester Stahlvorfächer | Titanium- & Stahlvorfächer
- Bester Reifen Gs 1250 – BMW R 1250 GS ADVENTURE (2019
- Beton Entsorgen Und Verwerten , Was will ich entsorgen? Beton
- Betriebsübergabe Mit Gleichstellungsgeld
- Betreuung Ablehnen | Antrag auf Entlassung aus Betreuung
- Betreutes Wohnen Dorsten Quellenbusch
- Bester Samsung Tv _ Der beste QD-OLED-Fernseher 2024: Samsung oder Sony?
- Betty Ong Absturz | Meet the Forgotten Asian-American Hero of 9/11
- Besteuerung Der Mütterrente Mit Einbezug