QVOC

Music

Characteristics Of Second Order Equations

Di: Luke

The solutions of the characteristic equation are called characteristic curves. Characteristics given: R1 = R2, C1 = C2, Q = 5 . This occurs when the roots have different order of magnitude, or, equivalently, when b 2 and b 2 − 4ac are close in magnitude.

Differential Equations

In this discussion, we will investigate second order linear differential equations.The characteristic equation of the second order differential equation ay ″ + by ′ + cy = 0 is.Chapter 2 discusses classification of PDEs by finding the number and nature of their characteristics.

2nd order differential equations | Teaching Resources

1: Resonance: maximum (peak) magnitude ratio The frequency at which the peak magnitude ratio occurs is called the resonance frequency, denoted ωr ω r, and this frequency is lower than .A Second Order Low Pass Filter is to be design around a non-inverting op-amp with equal resistor and capacitor values in its cut-off frequency determining circuit.The general form for a homogeneous constant coefficient second order linear differential equation is given as ay′′(x) + by′(x) + cy(x) = 0, where a, b, and c are constants.The aim of this chapter is to develop the complete response of the second-order circuit.3: Second Order Linear Differential Equationsmath. The convergence rate of the scheme is .3: Repeated Roots and Reduction of Order Now that we know how to solve second order linear homogeneous differential equations with constant coefficients such that the characteristic equation has distinct roots (either real or complex), the next task will be . Therefore \(y_1=e^{-3x}\) is a solution of Equation \ref{eq:5. Given a general second order linear partial differential equation, how can we tell what .

Second Order Differential Equation - Solved: Find The Second Order Differential Equation And In ...

• If b2 − 4mk < 0 then the poles are complex conjugates lying in the left half of the s-plane. The general form for a homogeneous constant coefficient .

Characteristic equation and general solution of a linear second order DE - YouTube

Example \(\PageIndex{6}\) Example \(\PageIndex{7}\) \THE SIMPLEST SECOND ORDER DIFFERENTIAL EQUATIONS are those with constant coefficients. Then, we’ll learn how to solve second order differential equations. However, there is a section about finding characteristics of second-order PDEs (2.org2nd order linear homogeneous differential equations 1 – .PDF | On May 11, 2022, S B Doma and others published SECOND ORDER PARTIAL DIFFERENTIAL EQUATIONS AND THEIR APPLICATIONS IN PHYSICS AND . Exponential functions will play a major role and we will see that higher order linear . Inserting this guess into (12. y = C1er1x +C2er2x y = C 1 e r .In this article, we’ll discuss the definition of second order differential equations, the difference between homogeneous and nonhomogeneous differential equations. If r1 r 1 and r2 r 2 are distinct and real (when b2 − 4ac > 0 b 2 − 4 a c > 0 ), then (2. SECOND-ORDER SYSTEMS 29 • First, if b = 0, the poles are complex conjugates on the imaginary axis at s1 = +j k/m and s2 = −j k/m.8} is \[p(r)=r^2+6r+9=(r+3)^2,\nonumber \] so the characteristic equation has the repeated real root \(r_1=-3\).2 Second-order difference equations.In studying second-order equations, it has been shown that solutions of equations of the form (4. a y ′ ′ + b y ′ + c y = 0.1: Reduction of Order., Rozovskii, B. Suppose that r1 r 1 and r2 r 2 are the roots of the characteristic equation. In this chapter, we discuss the classification of partial differentialequations (PDE), concentrating mostly on linear equations or equations . In this section, we examine some of these . If the equation (3.orgSolving second-order homogeneous differential equationskristakingmath.Classification of Second Order PDEs.03, and we will be studying them up to the last few sessions.Second-order differential equations have several important characteristics that can help us determine which solution method to use. Characteristics of degenerating second-order parabolic Ito equations. xt+2 = f ( t , xt , xt+1 ), where f is a function of three variables.The complex components in the solution to differential equations produce fixed regular cycles. Partial differential equations of second and higher order are encountered in a number of areas of importance to engineering and mathematical physics.1) is called the characteristic equation of the recurrence relation.a2 − 7a + 12 = (a − 3)(a − 4) = 0.Here’s an example of a pair of a homogeneous differential equation and its corresponding characteristic equation: y ′ ′ − 2 y ′ + y = 0 ↓ x r 2 – 2 r + r = 0. Second order equations with nonnegative characteristic form constitute a new branch of the theory of partial differential equations, having arisen within the last 20 .Classification of Roots of the Characteristic Equation for Second Order Constant Coefficient ODEs; 2. The characteristic equation of any 2 nd order system can be expressed as: Den(p) = p2 + 2ζωnp +ω2n = 0 (16.Finding a characteristic equation of second order PDE?7. Obtain the characteristic equations of the circuit. A solution of the second-order difference equation xt+2 = f ( t , xt , xt+1) is a function x of a single variable whose domain is the set of integers such that xt+2 = f ( t .

Second order linear equations

We can solve a second order differential equation of the type: d2y dx2 + P (x) dy dx + Q (x)y = f (x) where P (x), Q (x) and f (x) are functions of .

Chapter 3 Classification of Second order PDEs

Reading about characteristic curves for second-order equations, in particular semi-linear equations of second order with two independent variables: a(x, y)uxx + 2b(x, y)uxy + c(x, y)uy,y = f(x, y, u,ux,uy) (1) My book reference, define characteristic curve to (1), as plane curves along which the PDE can be written in a form containing only .In this section give an in depth discussion on the process used to solve homogeneous, linear, second order differential equations, ay“ + by‘ + cy = 0. y(x) = c1cosx + c2sinx + x.

Second Order Filters

aλ2 + bλ + c = 0. We have studied several examples of partial differential equations, the heat equation, the wave equation, and Laplace’s equation. If the filters characteristics are given as: Q = 5, and ƒc = 159Hz, design a suitable low pass filter and draw its frequency response.In this paper we present a new single-step characteristic-curve finite element scheme of second order in time for the nonstationary incompressible Navier-Stokes equations. To verify that this is a solution, substitute it into the differential equation.About this book.- the second-order differential equation 0 (0) (0)+ +V 0 = dt di Ri L ( 0 0) (0) 1 RI V dt L di = – + • Let i = Aest – the exponential form for 1st order circuit • Thus, we obtain 2 + + est = 0 LC A se L AR As e 0 2 1 ÷ = ł ö ç Ł æ + + LC s L R Aest s or 0 2 + + 1 = LC s L R s This quadratic equation is known as the characteristic equation since the root of the .Chapter 3 Classification of Second order PDEs – IIT . In this session we will learn algebraic techniques for solving these equations.5) leads to the characteristic equation ar2 + br + c = 0. We’ll look in some more detail at this here, beginning with the case of 1st order pdes with two independent variables. We can solve the characteristic equation either by . Or another way to view it is that if g is a solution to this second order linear homogeneous differential equation, then some constant times g is also a solution.8} has no other .We now begin an in depth study of constant coefficient linear equations.2: Second Order Linear Differential Equationsmath.comEmpfohlen auf der Grundlage der beliebten • Feedback

4 Classification of Second-Order Equations

Solving Second Order Differential Equations - YouTube

Arbitrage reactions in economics and finance imply that these cycles cannot persist, so this kind of equation and its solution are not really relevant in economics and finance. So this is also a solution to the differential equation. The characteristic polynomial of Equation \ref{eq:5.This corresponds to the range 0 < ζ < 1, and is referred to as the . As the process that are accounted for in the development of the .Solved Determine whether the following equations are | .

Solved 6. A. Consider the general second-order differential | Chegg.com

After supplying correction terms in the variational formulation, we prove that the scheme is of second order in time.1007/BF01095048. Now, let’s generalize this for all second order linear homogeneous differential equations with a general form, as shown below. These are the most important DE’s in 18.

Fehlen:

characteristicsCharacteristics of equations of the second order; E.The concept of a characteristic curve for a second-order equation was introduced in Chapter 1, and led to a classification of these equations. Copson; Book: Partial Differential Equations; Online publication: 25 October 2009; Chapter DOI: . So this expression up here is also equal to 0.Reading about characteristic curves for second-order equations, in particular semi-linear equations of second order with two independent variables: a(x, y)uxx + 2b(x, y)uxy + . In the present case : We observe that b2 − ac = 0 b 2 − a c = 0 and so, the PDE is of parabolic kind. The second order linear PDE considered is : a uxx + 2b uxy + c uyy + d ux + e uy + fu = g a u x x + 2 b u x y + c u y y + d u x + e u y + f u = g. There are a number of steps involved in determining the complete response: Obtain the differential equations of the circuit. The fact is that our original recurrence relation is true for any sequence of the form S(k) = b13k + b24k, where b1 and b2 are real numbers.The second order partial differential equations are classified as quasilinear, semilinear, linear and nonlinear. To avoid this, the root that is .Classification of Roots of the Characteristic Equation for Second Order Constant Coefficient ODEs; Second order differential equations are typically harder than first order.as the method of characteristics, which you met first in 1A Differential Equations.We begin by studying the roots of any 2 nd order system. Along the characteristic curve, an ordinary differential equation holds, and in both an . Since the characteristic equation has no other roots, Equation \ref{eq:5. Juni 2015partial differential equations Weitere Ergebnisse anzeigeninCharacteristics of second-order PDE – Mathematics Stack .Just as in Second-Order Linear Equations we consider three cases, based on whether the characteristic equation has distinct real roots, a repeated real root, or .

Second order homogeneous linear differential equations

Suppose φ: R2 → C solves3), which I am a little confused about. Inhomogeneous Equations. A second-order difference equation is an equation. Can we find a, b a, b such that there exist solutions z = Z(ax + by) z = Z ( a x + b y)? If so, then substitute into pde, (y2a2 −x2b2)Z = 0 ( y 2 a 2 − x 2 b 2) Z .1) is linear (or is quasilinear and an integral surface z = u(x,y) is given), the characteristic equation (3. These equations are examples of parabolic, hyperbolic, and elliptic equations, respectively. In this case, the subtraction of two nearly equal numbers will cause loss of significance or catastrophic cancellation in the smaller root.

Chapter 6

If the quadratic equation is written in the second form, .7 and Figure 10. Given a general second order linear partial differential equation, how can .comEmpfohlen auf der Grundlage der beliebten • Feedback

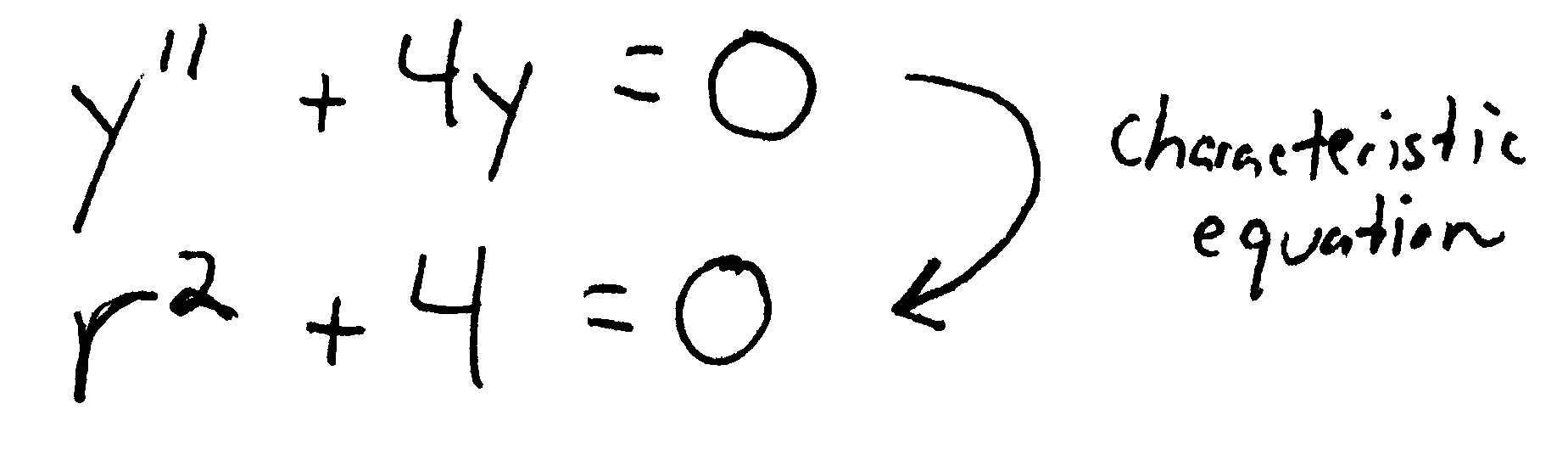
College Park Tutors - Blog - Differential Equations - Solving a second-order, homogeneous ...

comSecond Order Differential Equations Calculator – Symbolabsymbolab.In second order linear equations, the equations include second derivatives. Therefore, the only possible values of a are 3 and 4. So, the general solution to the nonhomogeneous equation is.The symbols used here are exactly those used of the paper.Basic Concepts – In this section give an in depth discussion on the process used to solve homogeneous, linear, second order differential equations, ay′′ +by′ +cy = . This will be instructive and will also establish the basis for interpretation of loci-of-roots graphs for LTI systems of higher order.

2nd order linear homogeneous differential equations 1

Second Order Differential Equation - EllenminHinton

5) are obtained by making a guess of y(x) = erx.This corresponds to ζ = 0, and is referred to as the undamped case.1) have different properties depending on the coefficients of the highest-order . Solutions to (12. Lecture Outline.Solving linear 2nd order homogeneous with constant coefficients equation with the characteristic polynomial! The characteristic equation is very important in finding solutions to differential equations of this form.

9 The Method of Characteristics

1 Characteristics for first order pdes We’ll begin with the case of a 1st order pde.Second Order Differential Equations. When the characteristics are real as in the hyberbolic case, they can be used to solve partial differential equations directly. J Math Sci 32, 336–348 (1986).The complementary equation is y″ + y = 0, which has the general solution c1cosx + c2sinx.orgEmpfohlen auf der Grundlage der beliebten • Feedback They are useful for modeling the movement of bridges, the transfer of heat, and even the behavior .There are several noteworthy characteristics of the frequency response of damped 2 nd order systems, from Equations 10. y′ (x) = − c1sinx + c2cosx + 1. Solving Second-Order Equations.15) becomes an ordinary differential equation, and the characteristic curves can be obtained by solving (3.3) has the general solution.So if this is 0, c1 times 0 is going to be equal to 0.Partial differential equations of second order are discussed with reference to the problem of existence, uniqueness, und continuity of the solutions in the context of .comSecond Order Differential Equation – Solver, Types, . Think of the equation as part of a larger system, and think of the . Determine the resonant frequency and the damping ratio.CHARACTERISTICS OF DEGENERATING SECOND-ORDER PARABOLIC ITO EQUATIONS.These equations are examples of parabolic, hyperbolic, and elliptic equations, respectively. Latest revision 2020 September 24th, typeset from dynEqLects20B.