QVOC

Music

Derivada Velocidad | Derivadas: definición y reglas básicas

Di: Luke

The Derivative

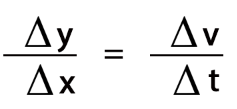
INTERPRETACIÓN GEOMÉTRICA Y FÍSICA DE LA DERIVADA - Curso para la UNAM

La derivada, una herramienta poderosa en el cálculo, desempeña un papel crucial en la comprensión y análisis de la velocidad y la aceleración.Identificar la derivada como el límite de un cociente de diferencia. Definición de la aceleración. La Calculadora de Derivadas soporta el cómputo de primeras, segundas, .v = ds , es decir : la velocidad representa la derivada (cambio) de la posición (s) dt con respecto al tiempo (t). Describir la velocidad como una tasa de cambio.

Cálculo Diferencial e Integral I: Velocidad y aceleración

Definición de la velocidad media y de la velocidad instantánea. ¿Qué representa la segunda derivada . Te ayuda a practicar mostrándote el procedimiento completo (diferenciación paso a paso).Introducción Para los problemas que veremos en esta entrada, será necesario recordar algunos conceptos de la Física relacionados con el Movimiento rectilíneo uniforme que posiblemente estudiaste en el bachillerato.La derivada es una generalización de la velocidad instantánea de una función de posición: si \(y = s(t)\) es una función de posición de un cuerpo en movimiento, nos \(s'(a)\) dice la . En el contexto de la velocidad, los puntos críticos son aquellos donde la derivada de la función de velocidad es igual a cero o no existe.La velocidad de deriva o de desplazamiento (También llamada velocidad de corrimiento) es la velocidad promedio que una partícula, como un electrón, alcanza debido a un campo . Descubrir recursos. Nomenclatura de Leibniz para .Las derivadas temporales: posición, velocidad, aceleración – YouTube.Para encontrar la velocidad máxima, debemos comprender la fórmula de la velocidad máxima.Cuando el movimiento es a lo largo de una línea recta, la posición viene dada por una sola variable, que denotamos por \(s(t)\text{.La fórmula de la primera derivada se basa en realidad en la idea de cambio relativo. Pensemos ahora que s D s. El punto de partida es la velocidad media: A este límite se lo conoce con el nombre de derivada. En la notación de cálculo diferencial se ., quintas derivadas así como diferenciación de funciones con muchas variables . La derivada del material se define para cualquier campo tensorial y que sea macroscópico, en el sentido de que depende solo de las coordenadas de posición y tiempo, y = y(x, t) : donde ∇ y es la derivada covariante del tensor, y u ( x, t) es la velocidad del flujo. Derivada de un producto: La derivada del primer término del producto es . Asimismo, la velocidad instantánea es igual a la derivada del vector posición respecto al tiempo.Regla de la cadena.3K views 3 years ago .25\text{,}\) y la velocidad promedio es \(-16 – 16(0. Publicado el 25 de mayo de 2023 por Pedro Castro Ortega.La velocidad de deriva o de desplazamiento (También llamada velocidad de corrimiento) es la velocidad promedio que una partícula, como un electrón, alcanza debido a un .

Calculadora de Derivadas • ¡Con pasos!

2: Posición, Desplazamiento, Velocidad. Representación Geométrica de las Identidades Trigonométricas

Derivadas: definición y reglas básicas

La derivada de una función es en sí misma una función, por lo que podemos encontrar la derivada de una derivada.comFB: http://bit.comEmpfohlen basierend auf dem, was zu diesem Thema beliebt ist • Feedback

Derivada

Velocidad instantánea en física con ejemplos

La derivada de una función describe la razón de cambio instantáneo de la función en un cierto punto. Estudiar Física Blog. De manera similar, se denomina “Aceleración” a la variación de la velocidad (v) con respecto al tiempo, por lo que para calcular dicha magnitud se debe derivar la función velocidad. En general, la derivada convectiva del campo u · y, la que . Recordemos que la velocidad se encuentra expresada por:begin{equation*}v=frac{d}{t}.

Como Calcular La Velocidad Instantanea Con Derivadas - Ecer

Esto nos permite calcular “la pendiente de . De forma similar sucede con la aceleración, para encontrarla es necesario derivar la función de velocidad, dicho en otras palabras es el cálculo de la segunda derivada de .}\) Por ejemplo, \(s(t)\) podría dar el marcador de milla de un automóvil que viaja por una . Velocidad en un momento específico = tasa de cambio instantánea en un momento específico = primera derivada en un momento . ii) La rapidez lineal del auto es: v = r・ω = 2 m ・2 rad/s = 4 m/s = 14,4 Km/h. Un uso frecuente de los ritmos de cambio consiste en describir .En matemáticas y cálculo, la derivada es una herramienta que nos ayuda a entender cómo cambia una función en un punto dado. Para la optimización de funciones, cálculo de máximos y mínimos.Este vídeo es parte de la playlist Entendiendo La Derivada, donde trato de explicar NO como hacer derivadas, más bien que hacen! Aquí les dejo el link a es.La velocidad es un ejemplo claro de magnitud derivada, ya que se obtiene a partir de la combinación de magnitudes fundamentales como la distancia y el tiempo.Para una línea mundial inercial (una con velocidad constante), definimos v = Δr/ Δ τ v = ∆ r / ∆ τ. Para obtener la .23K subscribers. Simplemente vamos a adivinar tal función y luego verificaremos que nuestra . Todo lo que queremos saber es en algún instante qué tan rápido está cambiando su distancia ( y) con respecto al tiempo ( x). ¿Qué son las derivadas? Las derivadas son reglas matemáticas que sirven para estudiar las funciones.Esta velocidad se puede calcular utilizando el cálculo para hallar la derivada de la posición del objeto con respecto al tiempo. El cálculo diferencial es la herramienta perfecta para expresar esta idea matemáticamente.La velocidad corresponde al cociente de las diferenciales espacio y tiempo, o incremento de la función e (t) dividido por el incremento del tiempo (t) cuando éste .ii) La rapidez lineal en cualquier instante. Sea un proyectil lanzado verticalmente desde el .Fórmula de la velocidad instantánea.

Derivadas y velocidad

Es decir, que el auto de juguete en todo instante tiene velocidad angular constante igual a 2 rad/s. De igual manera, una función es cóncava hacia abajo si su gráfica se abre hacia abajo (Figura 2. 539 views 7 months ago Curso de Derivadas. Esta figura muestra la concavidad de una función en varios puntos.

Derivada material

Para que veas cómo hallar este tipo de derivadas, vamos a resolver varios ejercicios a continuación: Derivada de una suma: Como puedes ver, para resolver la derivada de toda la función se ha aplicado la fórmula de la derivada de una potencia a cada término de la suma.75]\text{,}\) que dejamos \(h = 0. Cuando un objeto se mueve, la . En la presente clase aprenderemos como se realiza el calculo de la velocidad y aceleración usando derivada .Hallemos la derivada por definición de las siguientes funciones: Ejercicio 1: En este ejercicio aplicaremos la definición de la derivada mencionada anteriormente. En este video te muestro como el movimiento rectilíneo uniforme con ejercicios sencillos, te muestro como derivar . Solución: Hallando la derivada: dr V 6t 8t 3 2 dt .

Aplicación de derivadas - velocidad y aceleración ejemplo 1 - YouTube

El vector aceleración es la derivada del vector velocidad: Que también puede ser expresado en la forma: El vector aceleración es la variación del vector velocidad a lo largo del tiempo. A continuación, conoceremos la fórmula matemática y . En particular, la derivada . Conoce un conjunto de reglas muy útiles (como las reglas de potencia, .ly/VN7586 (NO OLVIDES DAR UN ¨LIKE¨)VISITA: http://math2me. Otra interpretación común es que la derivada nos da la pendiente de la . Por tanto debe apuntar siempre hacia dentro de la . Reescribimos f (x) Ahora vamos a desarrollar el producto notable.netVELOCIDAD Y ACELERACIÓN USANDO LA DERIVADA – .El vector velocidad es siempre tangente a la trayectoria de la partícula en cada punto de la misma. Por ejemplo, si tenemos una función que representa la posición de un objeto en función del tiempo, la derivada de . Nuestra calculadora te permite verificar tus soluciones a ejercicios de Cálculo.

Utilidades de la derivada en el análisis de velocidad y aceleración

Información generalEn las secciones anteriores definimos la derivada como la pendiente de una línea tangente, utilizando un límite particular.

Ejemplos de Calculo de Velocidad con Derivadas

Explicación de que es la derivada o el concepto de derivada explicándolo como la velocidad en un punto, teniendo en cuenta los incrementos, empezando con el . Además de preguntar si una función está aumentando o disminuyendo, también es natural indagar cómo una función está aumentando o disminuyendo.La derivada representa un papel fundamental en las Matemáticas debido a su gran cantidad de aplicaciones en la ciencia, la tecnología o la economía: Cálculo de la velocidad y la aceleración instantánea de cualquier objeto en movimiento. Hay tres comportamientos básicos que una función creciente puede demostrar en un intervalo, como se muestra en la Figura 1. En otras palabras, nos muestra la rapidez con la que la función está cambiando en ese punto.SUSCRÍBETE: http://bit.25) = -20\) pies/seg. Un problema relacionado con la velocidad.ly/FBmath2meG+: http://google. De modo que la fórmula de la velocidad instantánea es la siguiente:

Cálculo de Velocidad y Aceleración usando DERiVADAS

Velocidad instantánea: definición, fórmula, cálculo y ejercicios

com/+math2meTwitter: . Respuestas: i) La velocidad angular es la derivada de la posición angular: ω = φ’ (t) = 2. Otra interpretación común es que la derivada nos da la pendiente de la recta tangente a la gráfica de la función en ese punto.Ejemplos de derivadas. A través de fórmulas y cálculos, podemos determinar la . Gráficamente, una función es cóncava hacia arriba si su gráfica está curvada con la abertura hacia arriba (Figura 2.

Aplicaciones de la derivada: Posicion, velocidad y aceleracion. Ejemplo 1 - YouTube

3 Velocidad instantánea Si un móvil recorre 150 km en 2 horas, su velocidad promedio es v D vmedia defD espacio recorrido tiempo empleado D 150km 2h D 75km/h: Pero no conocemos la velocidad que lleva el móvil en un punto arbitrario de su trayectoria. Por ejemplo, la derivada de una función de posición es la .Para obtener la velocidad instantánea, fijémonos en un intervalo de tiempo tan pequeño como sea posible. Calcular la derivada de una función dada en un punto.La derivada 1 5.Geschätzte Lesezeit: 2 min

Aplicación de la derivada │ velocidad y aceleración

7: la función puede aumentar cada vez más rápidamente, .end{equation*}Esta igualdad modela el .En una gráfica distancia-tiempo, la velocidad .Así que, la velocidad instantánea, es la derivada de la función de la posición de un móvil, esta nueva función permite conocer la velocidad instantánea en cualquier momento del trayecto. Es una magnitud de gran importancia en diferentes áreas de estudio y nos permite medir y comprender el movimiento de los objetos.Para encontrar la velocidad, necesitamos encontrar una función de \(t\) cuya derivada sea constante.Posición, Velocidad y Aceleración con derivadas. En procesos productivos es .? Guía EXANI II 2024 Cálculo diferencial e integral: Aplicaciones físicas de la derivada #20? #exani2 #exani2024 #cursoexani2024 #uady2024 #uabcs #uabcs202.o, en el lenguaje del cálculo, la velocidad es la primera derivada de la distancia con respecto al tiempo. Matemáticamente, la velocidad instantánea se define como el límite de la velocidad media cuando el intervalo de tiempo tiende a cero.Hallar la derivada con respecto a “t”. La generalización a las líneas mundiales no inerciales requiere que hagamos de esta definición una derivada: v = dr dτ (3. Puntos Notables en un triángulo. Ejercicio 2: Aplicamos la definición.Derivadas y velocidad.1 Posición y velocidad media. Si no has tenido que lidiar con el cálculo, no te preocupes demasiado por esta definición. Aprende cómo definimos la derivada mediante límites.Aplicar derivadas en el cálculo de velocidad y aceleración de .t/ es una función que le asigna a cada tiempo t un .Por ejemplo, para obtener la velocidad promedio en \([0.Aplicación física de la derivada: velocidad y aceleración.Segunda Derivada y Concavidad. Aplicaciones de la derivada Velocidad y aceleración instantánea Ya se ha visto que la derivada sirve para calcular pendientes, pero también sirve para determinar el ritmo de cambio de una variable a otra, lo que le confiere utilidad en una amplia variedad de situaciones. Solución: El polinomio se puede escribir: x 2t 3t 5t 20 Aplicando la fórmula: dx 2(2)t 3(1)t 5(0)t 2 1 1 1 0 1 dt 4t 3 dt Ejemplo Ilustrativo 2: La posición de una partícula está dada por la ecuación: r 2t 4t 3t 5 32 (r en metros), hallar su velocidad instantánea cuando t 2 s. La cinemática es la parte de la mecánica que se ocupa de la descripción matemática del movimiento, dejando de lado la cuestión de qué causa que un objeto se mueva de cierta manera. Recta de Euler. Hay otras formas más sencillas de hallar la velocidad instantánea de un objeto en movimiento. Cualquier objeto en movimiento tiene una posición que puede considerarse una función del tiempo.

Cálculo de la velocidad instantánea por gráfica y por derivada - YouTube

La velocidad como la derivada de la distancia

En general, el valor máximo de una función ocurre en un punto crítico o en los puntos finales del intervalo.

Aplicación de la Derivada |Velocidad, Aceleración y Posición| - Salvador FI - YouTube

Derivabilidad de una función. (a+b)2 = a2 + 2ab + b2.