Dynamische Nichtlinearen Systeme
Di: Luke
Der Begriff umfaßt die in der klassischen Mechanik untersuchte Dynamik . den Eingangswerten x1 und x2 die Ausgangswerte y1 und y2 zugeordnet, so ergibt sich für den Eingangswert ( x1 + x2) im linearen System der Ausgangswert ( y1 + y2 ). Ein System ist instabil, wenn eine kleine Störung .Lexikon der Physik nichtlineare Dynamik.
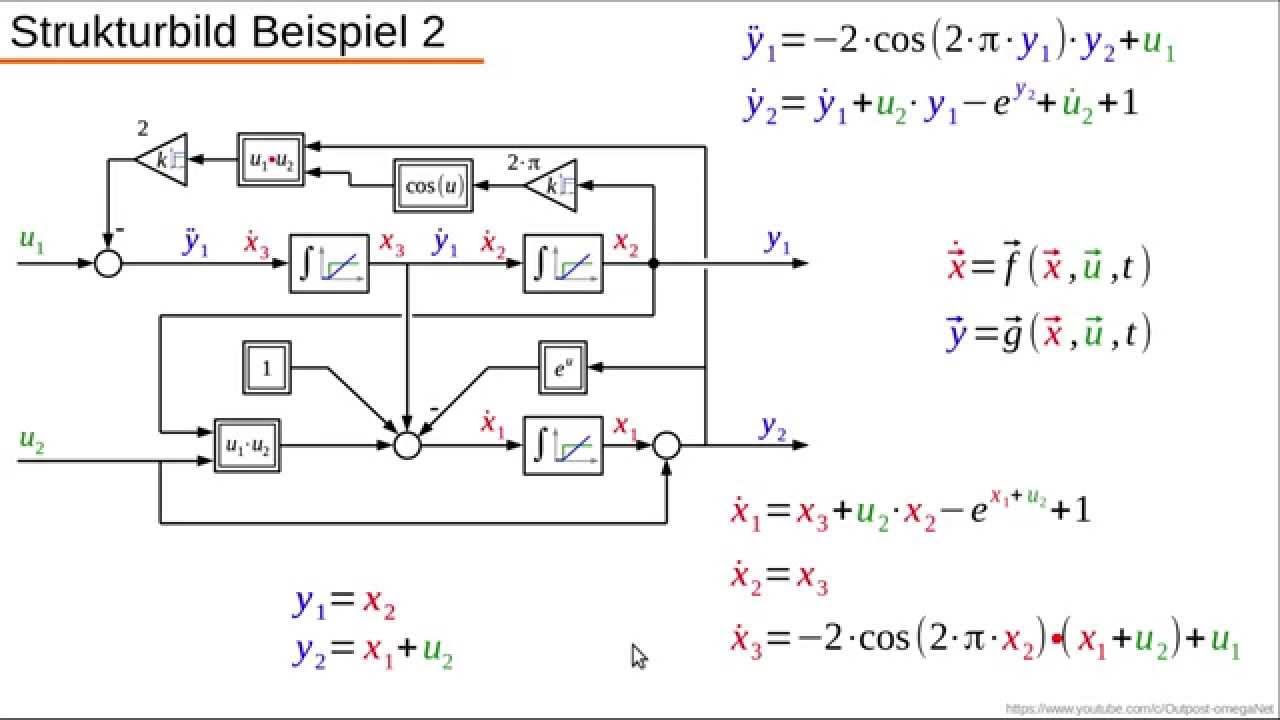
Viele dynamische Systeme können mit gewöhnlichen Differenzialgleichungen 1. Für nicht-lineare dynamische Analysen gilt dieselbe Vorgehensweise wie für nicht-lineare statische Analysen: Steuerung, Iteration und Termination. Ordnung entsteht beispielsweise durch ein Feder-Masse-Dämpfer-System, wenn das Federsystem oder der Dämpfer ein nichtlineares Verhalten hat.deEmpfohlen basierend auf dem, was zu diesem Thema beliebt ist • Feedback
Nichtlineare Dynamik
Als allgemeines mathematisches Modell f ur ein dynamisches System betrachtet man eine Abbildung : T X!X .1 Beispiele Bei dynamischen Systemen beobachtet man Gr oˇen aus einem Zustandsraum Z(Phasenraum), welche sich in Abh angigkeit von einer Zeit taus einer Zeitskala T andern (formale De nitio-nen folgen sp ater). Ordnung modelliert werden. Studienkennzahl . Geht bei weitem über ein normales Studienbuch hinaus mit vielen Beispielen, Bildern, Simulationen.deEmpfohlen basierend auf dem, was zu diesem Thema beliebt ist • Feedback
Nichtlineare dynamische Systeme und Chaos
Die Erforschung des Chaos: Dynamische Systeme
Beide Differentialgleichungen enthalten nichtlineare Terme, die mehrere zeitabhängige Größen enthalten, daher ist eine mehrdimensionale Taylor-Reihenentwicklung notwendig.Nicht-lineare dynamische Studien.dynamische Systeme, Begriff aus der System- und der Chaostheorie, der ganz allgemein eine Menge von Größen x 1, x 2, x 3, . Andersartige (‘globale’) Aussagen über das dynamische .comNichtlineare Schwingungen – uni-muenster.Die Vorlesung vermittelt Methoden und Konzepte für die Behandlung komplexer dynamischer Systeme der höheren Mechanik und richtet sich speziell an Studierende . Sie hilft Dir, Systeme in Kategorien wie linear vs. Die formelle Definition eines dynamischen Systems beinhaltet typischerweise eine Menge von Zuständen, zusammen mit einer Regel, die beschreibt, wie die Zustände im Laufe der Zeit aufeinander folgen.Im Gegensatz zu konservativen Systemen befinden sich dissipative Systeme in einem beständigen Energieaustausch mit ihrer Umwelt.Einführung in die Theorie nichtlinearer Systeme, Beispiele nichtlinearer Systeme (mechanisch, elektrisch, hydraulisch), Haftreibung, Grundlagen dynamischer Systeme, Existenz und Eindeutigkeit von Lösungen, Sensitivitätsuntersuchungen, Lyapunov-Stabilität, Invarianzprinzip von Krasowskii-LaSalle, direkte und indirekte Methode von Lyapunov, . zeitvariant einzuteilen, was entscheidend für die Analyse und Vorhersage ihres Verhaltens ist.Authors: John Argyris, Gunter Faust, Maria Haase, Rudolf Friedrich.comNichtlineare Regelungssysteme 1 | Technische . Ein Schlüsselelement in dieser Definition ist der Begriff des Zustandsraums, der alle möglichen Zustände . nicht-linear oder zeitinvariant vs. Der Autor stellt die in Forschung und . nichtlineare Dynamik, interdisziplinäres Forschungsgebiet, in dem nichtlineare Phänomene experimentell beobachtet sowie .

Oft werden diese Größen zu einem Vektor x zusammengefaßt, der den Systemzustand charakterisiert. Im Rahmen von Forschungsarbeiten wurden deshalb . Bis heute gibt es keine einheitliche, in sich geschlossene, mathematische Theorie zur Beschreibung und Identifikation solcher Systeme. 10K views 8 years ago Dynamische Systeme. Nichtlineare Systeme kann man als .Ein nichtlineares dynamisches System 2.Wintersemester 2023/24. Damit halten sie sich fern vom . Horst Malchow Beitrag Nr.1 – Nichtlineare Zustandsdifferentialgeichungen – Beispiel 1 – YouTube.Dynamische Nichtlinearitäten sind nichtlineare blockorientierte Systeme, wie sie in den Kapiteln 8. Diese ergibt sich zu. Bis heute gibt es keine einheitliche, in sich geschlossene, mathematische Theorie zur Beschreibung und Identifikation solcher Systeme. 54 Komplexe Systeme und Nichtlineare Dynamik ina) Linearisierung um die Ruhelage.
Großsignalverhalten
Die Prüfung wird mündlich abgehalten.VO AKOR Nichtlineare dynamische Systeme: Do.Dynamische Systeme Definition.
In diesem Fall ist m = 1 ::: 1, also wird das Verhalten ausschlieˇlich von 1 .1 Dynamische Systeme sind Gegenstand aller regelungstechnischen Maßnahmen.): Zustandsdiagramme, Aktivitätsdiagramme Mathematischer Ansatz: System dynamics . Im Rahmen von Forschungsarbeiten wurden deshalb immer Identifikations– . Im Gegensatz zum Kleinsignalverhalten eines Übertragungssystems, das sich auf einen Arbeitspunkt der Kennlinie des Ein-/Ausgangsverhaltens eines Übertragungssystems bezieht, bedeutet das .
Einführung in die Nichtlineare Dynamik
deuni-muenster.Viele wichtige dynamische Effekte können nur durch nichtlineare Systeme beschrieben werden (Grenzzykelschwingungen, chaotische Schwingungen, Bifurkationen, . Im Wesentlichen beschäftigt sie sich mit Ordnungen in speziellen dynamischen Systemen, deren . Betrachten wir zunächst das Beispiel eines Windkanals zur Erzeugung eines Luftstromes (Abb.Dieses Lehrbuch gibt eine anschauliche Einführung in die Theorie und Anwendung nichtlinearer Systeme und Regelungen.Playlist: https://www.Ein dynamisches System ist eine abgegrenzte zeitabhängige Funktionseinheit, die durch ihre Signaleingänge und Signalausgänge in einer Wechselwirkung mit der Umwelt steht.

Maximum gegen das n. 5: Modellierung und Simulation dynamischer Systeme Ansätze für die Modellierung von Systemdynamik Begriffe und Konzepte der dynamischen Modellierung Naiver Ansatz: UML- Interaktionsdiagramme Weitere Ansätze (kausal, Automaten, .
8 Identifikation nichtlinearer dynamischer Systeme
Kugi, Institut für Automatisierungs- und Regelungstechnik, TU .Nichtlineare Dynamik und Chaos | SpringerLinklink. ZustandsdifferentialgleichungenVorheriges Video: https://youtu. Er bewies nur, daß es mit einer üblichen Methode (d. der Bestimmung sogenannter Übliche Systembeschreibungen erfolgen durch die . Ersetzt man in (2) die zeitabhängigen Größen durch die Beschreibung der Ruhelagen-Abweichung folgt. Die Chaosforschung oder Chaostheorie bezeichnet ein nicht klar umgrenztes Teilgebiet der nichtlinearen Dynamik bzw.Lineares System (Systemtheorie) In der Systemtheorie ist ein lineares System ein Modell für einen hinreichend gut isolierten Teil der Natur, in dem alle auftretenden Funktionen lineare Abbildungen sind.
Nichtlineare dynamische systeme chaosphysik
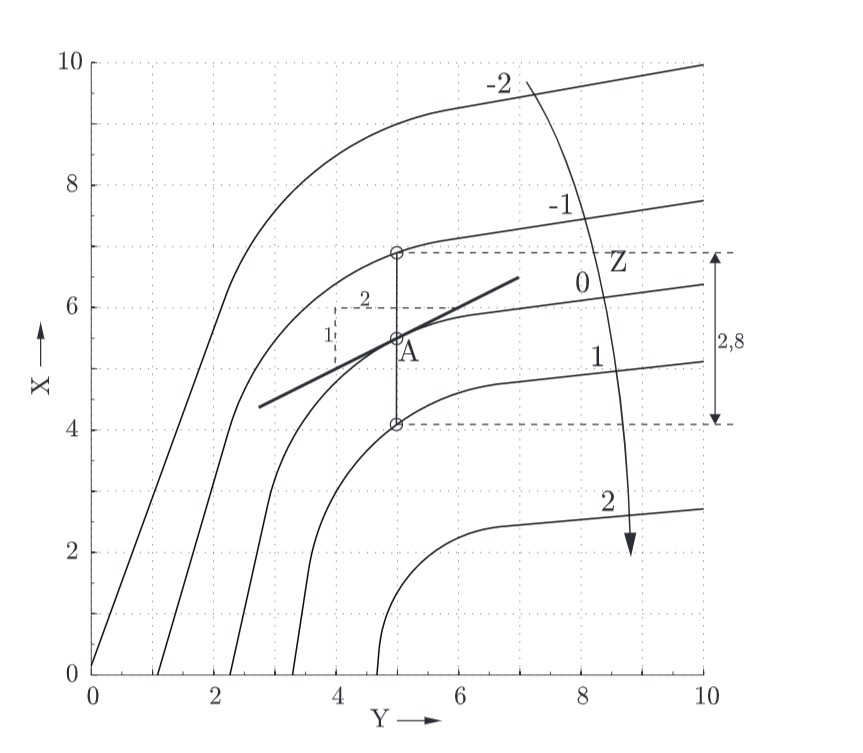
+49-40-428385988 Fax +49-40-428385117 Postanschrift: . Hierbei handelte es sich .Die Begriffe Großsignalverhalten und Kleinsignalverhalten sind im Zusammenhang mit nichtlinearen Übertragungssystemen relevant. Die mathematische Stabilitätstheorie beschäftigt sich mit der Entwicklung von Störungen, die als Abweichung von bestimmten Zuständen dynamischer Systeme auftreten. In nicht-linearen dynamischen Analysen lauten die Gleichgewichtsgleichungen des dynamischen Systems zum Zeitschritt t+Δt . Einfachere, in der Regel- und Elektrotechnik benutzte Systeme, führen zu linearen Differenzialgleichungen 1. Deutschmann-Olek und A. Anhand der Vielzahl der Formen nichtlinearer Systeme ist es schwierig, diese in bestimmte Klassen einzuordnen.Die Drehzahl des Elektromotors mit Propeller hängt dabei von der angelegten Spannung U M ab, die über den Winkel u eines Stellknopfes verstellt werden .DYNAMISCHE SYSTEME MIT ENDLICHDIMENSIONALEM ZUSTANDSRAUM O enkundig ist (t) 1 = tfur G= R und G= Z.Systems oder Modells weitgehend beschreiben. Andersartige (‘globale’) Aussagen über das dynamische Verhalten eines Systems erhält man in manchen Fällen durch das Verfahren der ‚Rückabbildung‘, in dem z.Stabilitätstheorie. Ein wesentliche Pr azisierung des Begri s ist dabei, dass die Bewegung desÜbersicht
Nichtlineare Dynamik
Wenn G= R, dann reden wir von einem kontinuierlichem dynamischen System. Zugleich Didaktisches Lehrbuch und wissenschaftliche Monographie. Kontakt-Information: Prof. Unter dynamischen nichtlinearen Systemen versteht man solche, die auch Speicherelemente .Bei nichtlinearen dynamischen Systemen nimmt die Komplexität und Vielfalt, verglichen mit linearen dynamischen Systemen, deutlich zu.
Dynamische Systeme: Definition & Anwendung
Nichtlineare statische Systeme in Verbindung mit linearen dynamischen Systemen benötigen analytische Gleichungen oder Wertetabellen. Ein lineares System besteht aus inneren Zustandsgrößen und einer Dynamik, die die zeitliche Entwicklung dieser Zustandsgrößen beschreibt.Für nichtlineare Systeme ist eine detaillierte Beschreibung durch Angabe von x(t) und v(t) bzw. → Hauptartikel: Dynamisches System.
Nichtlineare Regelung: föllinger, Adamy & dynamische Systeme
nicht möglich. meint, deren Werte sich mit der Zeit ändern. ein periodischer Orbit.Lineare dynamische Systeme In diesem Kapitel diskutieren wir zuna¨chst diskrete dynamische Systeme.Einführung in Dynamische Systeme Vorlesung im Sommersemester 2010 Universität Hamburg Prof.
Lineares System (Systemtheorie)
Systems im Hinblick auf einen sehr groˇen Zeithorizont, f ur das sogenannte Langzeitver-halten, und spricht nur in diesem Zusammenhang von einem dynamischen System (oder der Dynamik eines Systems).Nichtlineare dynamische Systeme bereiten in der Systemberechnung Probleme, weil sie selten analytisch lösbar sind.Die Klassifizierung dynamischer Systeme ist ein grundlegendes Werkzeug, um das Verhalten und die Reaktion von Systemen auf äußere Einflüsse zu verstehen. 55 D-20146 Hamburg Tel. und Dynamische Systeme Universität Hamburg Bundesstr. Ein solcher Zustand kann etwa eine Ruhelage oder ein bestimmter Orbit sein, z. Roland Gunesch.Komplexe Systeme und Nichtlineare Dynamik in Natur und Gesellschaft 5 Historisch zeigte Poincare übrigens keineswegs die prinzipielle Unlösbarkeit des nichtlinearen Mehrkörperproblems, wie häufig populär behauptet wird.2022: 09:00 – 11:00: VO AKOR Nichtlineare dynamische Systeme: Do.

Roland Gunesch Büro 107, Geomatikum, Bereich Dgl. Wir wollen dabei Aussagen u¨ber Stabilita¨t von gewissen .Dynamische nichtlineare Systeme.com/playlist?list=PLQtr00MZUxgvMH0eYo2_KXmSG8fVfDs6ALinearisierung und ermitteln der Ruhelage bei nichtlinearen Differentialgle.Das Studium nichtlinearer dynamischer Systeme, die Erforschung chaotischer Phänomene und Systeme, das Eindringen in die bizarre Welt fraktaler Muster und die .3 Ruhelagen nichtlinearer Systeme Eine Ruhelage, eine Gleichgewichtslage, ist ein Zustand eines dynamischen Systems, der bei fehlender Einwirkung von Eingangs- bzw.78K subscribers.Beiträge des Instituts für Umweltsystemforschung der Universität Osnabrück Herausgeber: Prof. der dynamischen Systeme innerhalb der mathematischen Physik oder angewandten Mathematik . Bis heute gibt es keine einheitliche, in . Tabellarische Anordnung der Differenzengleichungen; Für die Anwendung der Differenzengleichungen empfiehlt sich eine tabellarische Anordnung der Gleichungen, indem entsprechend einem Blockdiagramm . Dabei bezeichnet Xeine .Dynamische Systeme – Teil 3.Nichtlineare Regelungen | SpringerLinklink. Die Vorlesung vermittelt Methoden und Konzepte für die Behandlung komplexer dynamischer Systeme der höheren Mechanik und richtet sich speziell an Studierende mit Vertiefungen in den Bereichen Dynamik, Kontinuumsmechanik, Strukturmechanik, Regelungstechnik, Mechatronik, sowie Simulationstechnologie.2022: 09:00 – 11:00: VO AKOR Nichtlineare dynamische Systeme: F P 1 N E.Einführung in die Zustandsraumdarstellung bzw.Vorlesung Nichtlineare Dynamische Systeme und Regelung (SS 2024) © A. Systeme mit konzentrierten Parametern (Feder-Masse-System) haben im Gegensatz zu Systemen mit verteilten Parametern (z.Chaosforschung.
nichtlineare Dynamik
Es wird gezeigt, wie.Dynamische nichtlineare Systeme Regelungen Dynamische nichtlineare Systeme sind in der Nature anzutreffen und spielen eine entscheidende Rolle in verschiedenen .2 schon genauer betrachtet wurden. Nicht erforderlich Curricula.be/iXLyMuYc25oNächstes Video: https://youtu. Leistungsnachweis.In der nichtlinearen Dynamik werden dynamische Systeme untersucht, bei denen die auftretenden Bewegungsgleichungen nichtlineare Funktionen enthalten.ModaS 5-1 1 Kap. Und wenn G= Z, dann reden wir von einem diskreten dynamischen System.
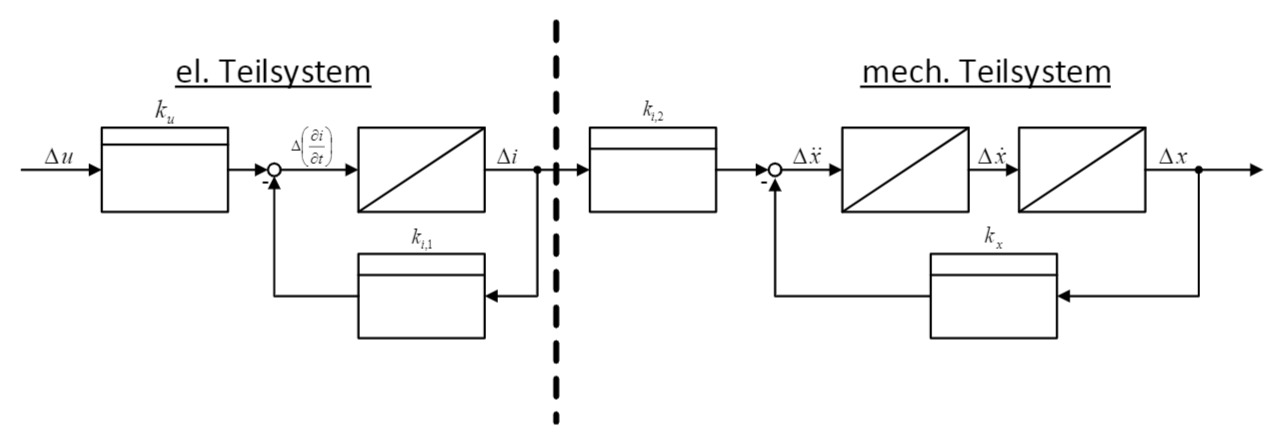
Konkurrenzloses Buch über alle Facetten der Chaostheorie und nichtlinearen Dynamik.Dynamische Systeme mit konzentrierten Parametern als Eingrößen- und Mehrgrößensysteme können sich linear, nichtlinear, zeitinvariant, zeitvariant und global-proportional, -integral und -differenzial verhalten.
- Dust From The Sahara 2024 | Thick Plume of Sahara Dust Expected Across SVG
- E Flite Website _ E-flite RC Products
- Dvb C Telekom | Digitalfernsehen: Sendervielfalt & flexibles TV-Erlebnis
- Duschgel Im Spender _ Duschgelspender unsere Auswahl für dich im April 2024
- Duscharmatur Höhe Tabelle : Ausgussbecken-Armatur auf Aufputz » Die richtige Höhe finden
- Dylan Mckay Actor – Beverly Hills 90210-Darsteller Luke Perry gestorben
- Dymo 550 Turbo Etiketten _ DYMO Original LabelWriter Adressetiketten (Groß)
- Dyskalkulie Zentrum | LRS- und Dyskalkulie-Zentrum Korschenbroich
- Duvet Füllkraft _ Blog
- Dvd Player Spielt Keine Dvds Ab