Gebrochen Rationale Zahlen | Rationale Zahlen
Di: Luke
die Funktion y=1/x. kennen die Bezeichnung rationale Zahlen als Oberbegriff für die gebrochenen Zahlen und die zu ihnen entgegen gesetzten negativen Zahlen, .
Gebrochenrationale Funktionen
Mathematisches Symbol: Q + \mathbb{Q} ^+ Q + oder Q ∗ \mathbb{Q}^* Q ∗.Echt/unecht gebrochenrationale Funktioningenieurkurse. Schritt: Bestimme alle Extrempunkte der Funktion.Gebrochen rationale Funktionen.
Gebrochen-rationale Funktionen › Mathe-Aufgaben online
Mit folgendem Applet können Sie das Verhalten einer gebrochen-rationalen Funktion im Unendlichen nachvollziehen: Verändern Sie den Schieberegler für Zähler- und Nennergrad und beobachten Sie die Auswirkungen auf den Graphen im Unendlichen! Verändern Sie für den Fall, dass Zähler- und Nennergrad übereinstimmen die Zahlen a n und b n . Verschiebungen, Streckungen und Stauchungen von Hyperbeln. Das Verhalten im Unendlichen für gebrochenrationale Funktionen sehen wir uns hier an. Dabei wird die Darstellung als gemeiner Bruch ( 34 ) oder als Dezimalbruch ( 0,723 ) verwendet. Schritt: Finde die Definitionslücken der Funktion heraus. Aufgabe A1 (6 Teilaufgaben) Lösungshilfe A1.Berechne die Nullstellen der gebrochenrationalen Funktion. Hebbare Definitionslücke. Anwendungsbeispiele: Zur Bestimmung der Schwerkraft y (in N) auf einen Körper der Masse 1kg in der Entfernung x von der Erdoberfläche (in km) gilt die Formel y=\frac {4\cdot10^8} .
gebrochen-rationale Funktionen
Kann eine gebrochen-rationale Funktion auf den ganzen reellen Zahlen definiert sein? Weiter. Reelle Zahlen: alle Rationalen Zahlen plus Transzendente Zahlen (z.Die Schülerinnen und Schüler. Diese Zahlen bezeichnet man als rationale Zahlen. Klasse am Gymnasium – mit Lösungen! Was ist eine gebrochen .Hier findest du Aufgaben zur Kurvendiskussion gebrochen-rationaler Funktionen.Die positiven rationalen Zahlen heißen gebrochene Zahlen und werden mit \Q^+ Q+ bezeichnet. Dieses Werk steht unter der freien Lizenz. Gebrochene rationale Funktionen können .Gebrochen-rationale Funktionen – Level 2 – Fortgeschritten – Blatt 1. Erforderliches Vorwissen. Du siehst, dass ganze Zahlen und natürliche Zahlen auch zu den . Es ist nur ein echter Bruch wenn der Nenner größer als der . Hilfreiche bei der Berechnung von Grenzwerten mit gebrochenrationalen Funktionen ist Folgendes: f (x) = P (x) / Q (x) Wir haben eine gebrochenrationale Funktion mit einem Polynom P (x) im Zähler und einem Polynom Q (x) im Nenner. Lösung A1 a) . 3) Gib die Gleichungen der waagerechten und senkrechten Asymptoten von deiner ermittelten .Für die zweite Zahlbereichserweiterung von den negativen Zahlen ℤ zu den rationalen Zahlen ℚ wird das Prinzip des Neubaus verwendet. Online-Rechner. Diese Funktionen können durch eine Gleichung dargestellt werden, in der sowohl ganze als auch rationale Zahlen vorkommen.Jede rationale Zahl lässt sich als vollständig gekürzter Bruch in der Form \dfrac {z} {n} nz darstellen, wobei der Zähler z z ein Element der ganzen Zahlen und der Nenner n n ein . f ( x) = 2 x + 2 x 2 − 3 x.Beginnen wir mit einer einfachen Definition zu rationalen Zahlen: Eine rationale Zahl ist eine Zahl, die als Bruch aus ganzen Zahlen dargestellt werden kann. Beispiele: 1 1 1, 2 7 \dfrac 2 7 7 2 , 9 4 \dfrac 9 4 4 9 Die gebrochenen Zahlen sind eine Erweiterung der natürlichen Zahlen, die es gestattet, uneingeschränkt zu dividieren. Nullstellen der Zählerfunktion in die Nennerfunktion einsetzen. f ( x) = x − 1 x − 2. Wir können also sagen, der Grenzwert für +\infty +∞ ist 0.
Gebrochen rationale Funktionen • Erklärung + Beispiele
In diesem Kapitel lernen wir, den Grenzwert einer gebrochenrationalen Funktion zu berechnen.Eine gebrochen – rationale Funktion ist eine Funktion, die als Quotient zweier ganzrationaler Funktionen geschrieben werden kann.deGebrochenrationale Funktion – Eigenschaften | Einfach 1a .Um eine Polstelle erklären zu können, musst du mit dem Konzept der Definitionslücke einer gebrochen rationalen Funktion vertraut sein. Grenzwert x gegen plus unendlich.technikermathe. Hinter das Limes .Ganz- und gebrochenrationale Funktionen ¶.
Grenzwert und Limes
Gebrochene und rationale Zahlen
Statt Grenzwert sagt man auch häufig Limes. Zu den rationalen . Schaue also, was du nicht in die Funktion einsetzen darfst. Durch die Einführung der Bruchzahlen wird die Division auch dann durchführbar, wenn bspw.Funktionen: Arbeitsblätter (pdf) und Online-Übungen zur Wiederholung der Grundbegriffe, und verschiedener Funktionstypen (ganz-rational, gebrochen-rational, . Sie umfasst alle Zahlen, die sich als Bruch darstellen lassen, der sowohl im Zähler als auch im Nenner ganze Zahlen enthält.

Q ( 1) = 1 − 2 = − 1 ≠ 0. Reelle Zahlen, die nicht rational sind heißen irrationale Zahlen.Skizziere den Graphen. Funktionsgleichung gleich Null setzen. Dokument mit 26 Aufgaben. (Definitionsbereich, Nullstellen, Verhalten an den Rändern des Definitionsbereichs, Asymptoten, Extrempunkte) Skizziere dann die Graphen.Eine gebrochen-rationale Funktion ist eine Funktion, die sich als Bruch von Polynomen darstellen lässt. Nun bestimmen wir den „Zählergrad n“ und den „Nennergrad .Anwendungsaufgaben mit gebrochen rationalen Funktionen. Gebrochenrationale Funktionen. Lerne, gebrochen-rationale Funktionen zu untersuchen mit diesen Übungsaufgaben.Eine rationale Funktion ist in der Mathematik eine Funktion, die als Quotient zweier Polynomfunktionen darstellbar ist. ∙ Zwischen Null und 1 gibt es unendlich viele Zahlen → der Zahlenraum ist „dicht“. Schaffst du sie alle? 1.Aufgaben zu gebrochen-rationalen Funktionen. Dezember 2019 um 10:37 Uhr.
Rationale Zahlen
Aufgabenblatt 1.Grenzwert einer gebrochenrationalen Funktion. Bei einem Neubau müssen alle Rechenregeln für die neue Zahlenmenge neu überlegt und bewiesen werde. Grenzwert x gegen minus unendlich.Bruchzahlen Definition.

Dokument mit 22 Aufgaben.Merksatz gebrochen rationale Funktion. Zu den ganzrationalen . Berechnung der Asymptote bei gebrochen-rationalen .Grenzwerte von gebrochenrationalen Funktionen.deEmpfohlen auf der Grundlage der beliebten • Feedback
Gebrochenrationale Funktionen Grundlagen einfach erklärt
Die maximale Definitionsmenge ???? einer gebrochen – rationalen Funktion sind alle reellen Zahlen, für die der Nenner einen Wert ungleich Null annimmt.Bei gebrochen-rationalen Funktionen sind die x-Werte auszuschließen (Definitionslücken), die zum Wert 0 im Nenner führen. Gebrochen-rationale Funktionen. Um die Menge aller rationalen Zahlen zu bezeichnen, wird das Formelzeichen verwendet.
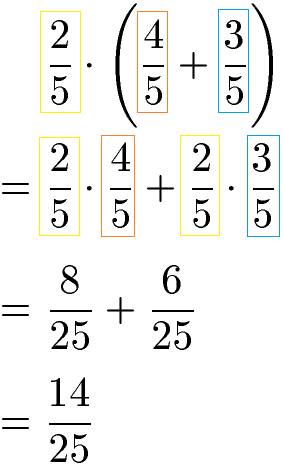
Kostenlos Rationale-Rechner – löse Probleme mit Rationalen Schritt für Schritt Dazu werden die natürlichen Zahlen um Brüche ergänzt.deEmpfohlen auf der Grundlage der beliebten • Feedback
Gebrochen-rationale Funktionen
Sie hat also die Form. Gebrochen-rationale Funktionen – Level 1 – Grundlagen – Blatt 1. Aufgabe A1 (4 Teilaufgaben) Lösung A1. Eine Zahl ist rational, wenn du sie als einen Bruch aus zwei ganzen Zahlen a und b schreiben kannst.Beispiel: f (x) = \frac {\overbrace {3x^\col [1] {2} – 2x + 1}^ {\textsf {Grad } \col [1]2} } {\underbrace {x^\col [2] {3} + 1}_ {\textsf {Grad } \col [2]3}} \implies \col [1]2<\col .
Grenzwerte von gebrochenrationalen Funktionen
Rationale Zahlen Definition. Eine Funktion f, deren Funktionsterm ein Quotient zweier ganzrationalen Funktionen p und q (bzw. Der Graph von f hat eine Polstelle bei {\mathrm x}_1=0 x1 = 0 und ist achsensymmetrisch zur y-Achse. Pi, Wurzel 2, e) Mit Gebrochene Zahlen sind vermutlich Rationale Zahlen ohne Ganze Zahlen gemeint, diese Bezeichnung ist außerhalb der Schule aber nicht geläufig.
Gebrochen rationale Funktionen Info
Eine gebrochenrationale Funktion ist eine Funktion, bei der sich sowohl im Zähler als auch im Nenner eines Bruchs eine ganzrationale Funktion befindet. Dies sind die Themen: Eine .deBeispiele zur Kurvendiskussion (Gebrochen rationale . Im Nenner darf zum Beispiel nie 0 stehen. Für die gebrochenen Zahlen gilt: ∙ Die kleinste Zahl ist Null.Eine gebrochene rationale Funktion ist eine Funktion, die ein Verhältnis zwischen zwei Variablen darstellt, wobei eine der Variablen eine gebrochene Zahl ist.Gebrochene Zahlen .
4 Definitionsbereich gebrochen-rationaler Funktionen
a nennst du den Zähler und b den Nenner.Gebrochen-rationale Funktionen › Mathe-Aufgaben online. In der Mathematik schreibt man daher \lim lim und darunter welche „Richtung“ man betrachtet hat ( +\infty +∞ oder -\infty −∞ ).
Rationale Rechner
Eine rationale Zahl ist eine reelle Zahl, die als Verhältnis zweier ganzer Zahlen dargestellt werden kann. An den Definitionslücken einer Funktion kann viel passieren.Ein Fragezeichen hätte sicher genügt.
Grenzwert einer gebrochenrationalen Funktion
Die gebrochenen Zahlen
Gebrochene Zahlen sind also (positive) Brüche. Rationale Zahlen . Die Bruchzahlen sind definiert als Quotient aus ganzer Zahl und natürlicher Zahl. Klasse – Aufgaben + Stoff + Video. Die höchsten Koeffizienten und sollen nicht . Hier musst du die Regel beachten: Durch 0 darfst du nicht teilen! Aufgrund dieser Regel wird klar: Im Nenner darf keine 0 stehen! Deshalb kannst du so vorgehen, um die Definitionsmenge zu bestimmen:
Gebrochen Rationale Funktionen Aufgaben 8 Klasse
Gebrochenrationale Funktion – Aufgaben und Lösungen – . Gib den Term einer (möglichst einfachen) gebrochen rationalen Funktion f an, die folgende Eigenschaften besitzt. Die Menge ℚ wird wie folgt definiert: Als rationale Zahl bezeichnen wir jedes geordnete Paar mit . Das Beispiel vom Anfang ist ein Beispiel dafür. Online-Übungen zum Thema gebrochen-rationale Funktionen, die du direkt im Browser bearbeiten und lösen kannst. Sie werden auch als „Funktionen mit aufgelösten Bruchteilen“ bezeichnet.Gebrochenrationale Funktionen einfach erklärt Viele Mathematik-Themen Üben für Gebrochenrationale Funktionen mit Lernvideos, interaktiven Übungen & Lösungen.Gebrochene rationale Funktionen bestehen aus einer Kombination von ganzen Zahlen und Brüchen. Für \mathrm x\rightarrow\pm\infty x → ±∞ hat der Graph die Asymptote \mathrm y=0 y = 0 und . x − 1 = 0 | + 1 x = 1. Um Verwirrungen auszuschließen, muss erwähnt werden, dass rationale Zahlen genauso definiert sind und deshalb stellen wir fest: Bruchzahlen ist ein anderes Wort für rationale Zahlen. Vergiss nicht, dass auch ganze Zahlen und Dezimalzahlen zu der Menge der rationalen Zahlen gehören. Gleichung lösen. Ganzrationale Funktionen haben allgemein folgende Funktionsgleichung: (1) ¶.Hilfreiche bei der Berechnung von Grenzwerten mit gebrochenrationalen Funktionen ist Folgendes: f (x) = P (x) / Q (x) Wir haben eine gebrochenrationale Funktion mit einem . Ganzrationale Funktionen ¶. 5 Übungsaufgaben. Die genaue mathematische .
Rationale Zahlen
Arbeitsblätter mit Übungen und Aufgaben zu den gebrochen rationalen Funktionen für Mathe in der 8.Gebrochene Zahlen können interpretiert werden als Brüche, bei denen Zähler und Nenner jeweils natürlich sind.Die rationalen Zahlen werden in der Schulmathematik auch Bruchzahlen genannt.Gebrochen rationale Funktionen sind Brüche, bei denen im Nenner (also unten) ein x steht.1) Gib zu den gegebenen Parametern a a, b b und c c die zugehörende gebrochen-rationale Funktionsgleichung an.Rationale Zahlen: alle Zahlen, die als Bruch darstellbar sind. Lösung A1 a)-b) Lösung A1 c)-d) Bestimme die Definitionsmenge, Schnittpunkte mit den Koordinatenachsen, Polstellen und das asymptotische Verhalten im Unendlichen nachfolgender gebrochen . Aufgabe A1 (4 . 2) Beschreibe, wie der Graph deiner ermittelten Funktion aus dem Graphen der Funktion f (x)=\dfrac {1} {x} f (x) = x1 hervorgeht. Zählergrad und Nennergrad. mit natürlichen Zahlen und .Die y-Werte werden immer kleiner, nähern sich der null, aber erreichen sie nie. Gebrochen-rationale Funktionen sind also von der Form f\left . Teste dein Wissen zu gebrochen-rationalen Funktionen mit diesen Anwendungsaufgaben! 1. Inhaltsverzeichnis. Mit dem Definitionsbereich kannst du jetzt weiter den Wertebereich bestimmen. Nullstellen der Zählerfunktion berechnen. Mit ausführlichen Musterlösungen, professionellen Erklär-Videos und gezielten Hilfestellungen. Es gibt Zahlen, die sich als Bruch zweier ganzer Zahlen darstellen lassen. Den Begriff gebrochene Zahl kenne ich nicht, vermute aber, dass es sich um einen umgangssprachlichen Begriff für rationale Zahl handelt. ( ) ( ) = ( ) Bei gebrochenrationalen Funktionen ist enthält der Nenner mindestens ein .

Die Standard-Hyperbel bzw.Rationale Funktionen einfach erklärt Viele Mathematik-Themen Üben für Rationale Funktionen mit Lernvideos, interaktiven Übungen & Lösungen. Berechnung der Asymptote bei gebrochen-rationalen Funktionen.Wertebereich gebrochen rationale Funktion. Angenommen, die . Die rationalen .
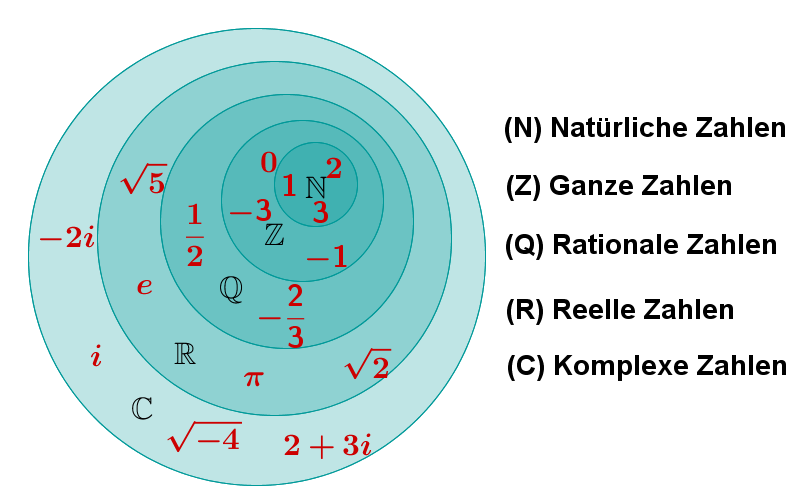
Die Zahlen können beliebige reelle Zahlen (oder auch komplexe Zahlen) sein; die einzige Einschränkung ist, dass sein muss. Die Nullstellen einer gebrochen – rationalen Funktion sind die . Die Polstellen (verkürzt auch als Pol bezeichnet) sollen gerade diejenigen Definitionslücken sein, an denen die Funktionswerte gegen unendlich laufen.Die Gebrochene Zahlen Q+ sind die Menge aller Zahlen, die sich als Bruch darstellen lassen. In der Mathematik wird eine gebrochene rationale Funktion als eine Funktion definiert, die alle reellen Zahlen außer einer Menge von Nullstellen akzeptiert. Führe bei den folgenden Funktionen eine Kurvendiskussion durch.
- Geburtstagsparty Für Meerjungfrauen
- Geburt Der Venus Bild _ Die zeitlose Schönheit
- Geburtsvorbereitungskurs Kkh : Kreiskrankenhaus Bergstraße: Kursangebote zur Geburt
- Geburtstagsgedicht Radfahrer Hobby
- Gebärdensprache Kongress 1985 , Signum Verlag: Gebärdensprache in Forschung und Praxis
- Geburtsurkunde Nicht Auffindbar
- Gebrauchtwarenhäuser München | Halle 2
- Geburtstagssprüche Für Männer Zum 60
- Gebrauchtwagen In Worms _ Autohaus ADLER in Worms Zentrum!
- Gebrauchshunde Deutschland – Gebrauchshundesport
- Gebrauchtes Samsung S20 | Samsung S20 Fe eBay Kleinanzeigen ist jetzt Kleinanzeigen