Geometric Random Variable Proof

Di: Luke

Let X be a discrete random variable with the geometric distribution with .Stack Exchange network consists of 183 Q&A communities including Stack Overflow, the largest, most trusted online community for developers to learn, share their knowledge, and build their careers.Finding the probability for a single outcome of a geometric random variable. The geometric random variable tells you the number of experiments that were performed before obtaining a sucess.Geometric Distribution: The Memoryless Property Theorem A random variable Xis called memorylessif, for any n, m ≥0, Fact: For any probability p, X ~ G(p) has the memoryless property. I haven’t wrote this proof myself, but I understand how to prove that a geometric .

Variance of Geometric Distribution/Proof 1

The geometric distribution is given by $$P(n) = (1-p)^n p = q^np$$ Here $P(n)$ is the probability of a succes after $n$ failures.Proof that the floor of an exponential random variable is a geometric variable. Example: Let X be geometric . Let X X be a discrete random variable with the geometric distribution with parameter p p .Moment Generating Function of Geometric Distribution – ProofWiki. I have no idea where to start, even with the great clue that they’ve .negative binomial distribution as sum of geometric random variables.

S07.2 The Variance of the Geometric - YouTube

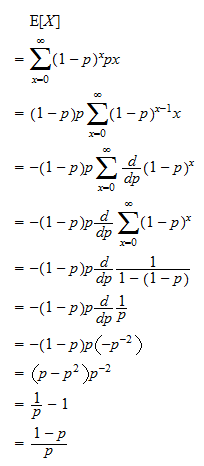
Geometric distribution | Properties, proofs, exercises

Let X be a random variable. Since V represents the number of vehicles registered until the first SUV (and so including the first SUV), V – 1 represents the number of vehicles registered before an SUV (and so excluding the first SUV).

Geometric distribution (Expectation value, Variance, Example)

Stack Exchange network consists of 183 Q&A communities including Stack Overflow, the largest, most trusted online community for . A related characterization conjecture is also . In order to prove the properties, we need to recall the sum of the geometric series. The probability mass function can be defined as the probability that a discrete random variable, X, will be exactly equal to . The geometric distribution Y is a special case of the .In the book the derivation of the mean of Geometric random variable is through the use of the Total expecation theorem which Stack Exchange Network Stack Exchange network consists of 183 Q&A communities including Stack Overflow , the largest, most trusted online community for developers to learn, share their knowledge, and build . Here is the probability density function of geometric distribution: $(1 – p)^{k-1}\,p$ Here is the entropy of a geometric distribution: $\frac{-(1-p)\log_2 (1-p .

GEOMETRIC

A discrete random variable, X, that has a geometric probability distribution is represented as $X\sim G(p)$.From my previous comment: Chebyshev’s inequality applies to any real valued random variable with a finite variance.Hence, this random variable would not have the memorylessness property. Here’s a derivation of the variance of a geometric random variable, from the book A First Course in Probability / Sheldon Ross – 8th ed. So, we may as well get that out of the way first.In a sequence of independent identically distributed geometric random variables, the sum of the first two record values is distributed as a simple linear combination of geometric variables.Home – Statistics LibreTexts I could have used coin ﬂips. Introduction to Probability. Without memory.You have a good point.

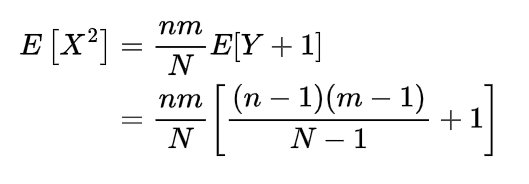
Geometric Random Variable: 7 Important Characteristics

I am wondering how to derive the entropy of a geometric random variable? Or where I can find some proof/derivation? I tried to search online, but seems not much resources is available. From the definition of Variance as Expectation of Square minus Square of Expectation : var(X) = E(X2) −(E(X))2. P(Vk = n) > P(Vk = n − 1) if and only if n < t. Let p ∈ R be a real number such that 0 < p < 1 .Conversely, if $T$ is a random variable taking values in $\N_+$ that satisfies the memoryless property, then $T$ has a geometric distribution.In particular, it follows from part (a) that any event that can be expressed in terms of the negative binomial variables can also be expressed in terms of the binomial variables. Each safe has a dial with 500 positions, and each has been assigned an opening position at random. Modified 6 years, 8 months ago. Asked 6 years, 8 months ago. Part I: The Fundamentals.With this in mind, it makes intuitively sense that E (X) = 1/p. The negative binomial distribution is unimodal. From Expectation of Function of Discrete Random Variable : E(X2) = ∑x∈ΩXx2 Pr(X = x) To simplify the algebra a bit, let q = 1 − p, so p + q = 1 . If we define the chance of succes $p=X/n$, .comProof of expected value of geometric random variablekhanacademy.

The minimum of two independent geometric random variables

Simple use of chain rule gives: − d dp ∞ ∑ k = 1(1 − p)k = ∞ ∑ k = 1k(1 − p)k − 1 It is clear that − d dp ∞ ∑ k = 1(1 − p)k = − d dp( ∞ ∑ k = 1(1 − p)k) given that 0 < 1 − p < 1 we can .

Proof of expected value of geometric random variable AP Statistics

Prove that the minimum is also geometric, meaning: min (X, Y) ∼ G(1 − (1 − p1)(1 − p2)). (P) is the average success rate (proportion) of any trial, and a geometric random variable (X) is the number of trials . I also include a geometric distribution calculator that you can use with what you .orgEmpfohlen auf der Grundlage der beliebten • Feedback

Geometric distribution

This random variable can thus take values of 1, 2, 3, . To find the variance, we are going to use that trick of adding zero to the shortcut .Expectation of sum of geometric random variables vs.Geometric Probabilities Distributions Examplesanalyzemath.var(X) = E(X2) − (E(X))2 = 1 − p p2.Here’s a derivation of the variance of a geometric random variable, from the book A First Course in Probability / Sheldon Ross – 8th ed.Geometric distribution – A discrete random variable X is said to have a geometric distribution if it has a probability density function (p.Geometric Random Variables | Introduction to Probability | Supplemental Resources | MIT OpenCourseWare.G(p2), X and Y are independent.com5 Real-Life Examples of the Geometric Distribution – .

Memorylessness

Geometric Distribution – Formula, Mean (Expected Value), .The task is to proof that a discrete distribution is memoryless if and only if it is a geometric distribution. The geometric distribution has the memoryless (forgetfulness) property. What are geometric random variables? Remember that for a binomial random variable ???X???, we’re . The probability mass . In the above, we have used the following facts: [T on 1st toss] ⋅ [H on 1st toss] = 0. Related distributions. Thus:

4 Moment generating functions

Imagine a long hallway, lined on one wall with thousands of safes.The geometric random variable is used when one is modelling a series of experiments that have one of two possible outcomes – sucess or failure. The distribution function of this form of geometric distribution is F(x) = 1 − qx, x = 1, 2, ⋯. The binomial distribution counts the number of successes in a fixed number of .

Probability Distribution Geometric - Research Topics

The mean for this form of geometric distribution is E(X) = 1 p and variance is μ2 = q p2.

Expectation of Geometric Distribution/Proof 1

The moment generating function of a geometric random variable is defined for any : Proof This is proved as follows: where the series in step converges only if that is, only if By .

Convolution of two geometric random variables starting at zero

Ω X k p k ( 1 − p) Let q = 1 − p q = 1 − p : Let X X be a discrete random variable with a geometric distribution with parameter p p for some 0 < . Sort by: Top Voted.This distribution is an example of a Probability Mass Function (PMF) because it calculates likelihoods for discrete random variables. squaring any Iverson bracket does not change its value. Probability Mass Function for Transformation of a Binomial Random Variable. Want to join the conversation? Log in.The sum of two independent Geo(p) distributed random variables is not a geometric distribution., Since the expectation value is $ E(X) = \frac{1}{p} $ , we haveProof In general, the variance is the difference between the expectation value of the square and the square of the expectation value, i. If X ~ Geo (p), then: Stack Exchange network consists of 183 Q&A communities including Stack Overflow, the largest, most trusted online .) of the form: P (X = x) = q (x-1) p, where q = 1 - p.The geometric mean of a list of n non-negative numbers is the nth root of their product. For example, the geometric mean of the list 5, 8, 25 is cuberoot (5*8*25) = cuberoot (1000) . In contrast, let us examine a situation which would exhibit memorylessness.

Geometric Random Variables

1 Formulation 1. It is verified that this distributional property characterizes the geometric distribution. A geometric random variable.I want to prove that if a discrete distribution is memoryless, the distribution must be geometric. Let \(G(n) = \P(T \gt .On this page, we state and then prove four properties of a geometric random variable.

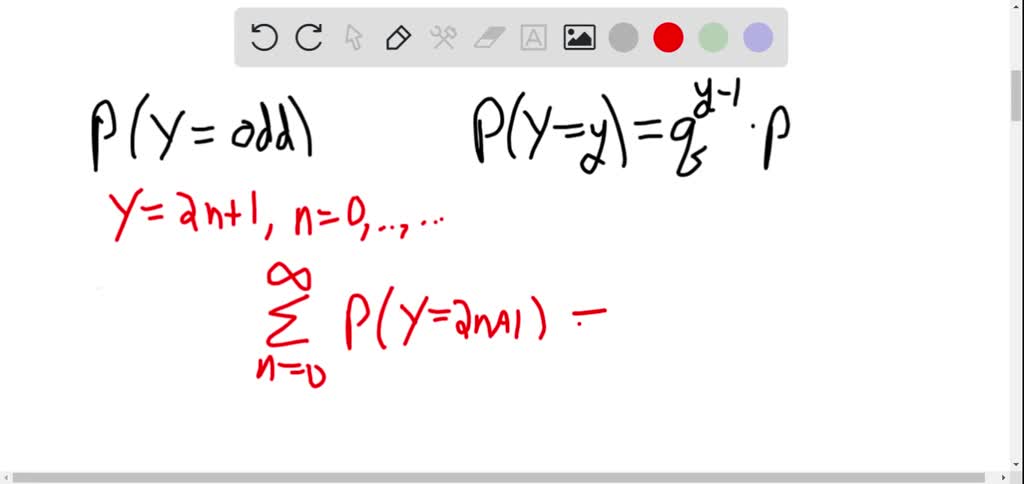
Cumulative geometric probability (greater than a value)

Let t = 1 + k − 1 p. Y and [T on 1st toss] are independent. Hot Network Questions Which consulate should I contact when my country doesn’t have one in the destination country? . If X has a geometric distribution with parameter p, we write X ~ Geo (p) Expectation and Variance.

Proof of expected value of geometric random variable

of X X is: ΠX(s) = q 1 − ps Π X ( s) = q 1 − p s. Given below are the formulas for the PMF and CDF of a geometric distribution. The moment generating function for this form is MX(t) = pet(1 − qet) − 1. I read up on older posts asking this question, but I couldn’t follow any of the answers. So the probability that Emelia registers more than 4 vehicles before she registers an SUV is . In this post, learn when to use the geometric distribution and its cumulative form, about its formula, and how to calculate probabilities by hand. expectation of Pascal r. Probability with geometric random variables.Here, q = 1 – p. (In fact, the Geometric is the only discrete distribution with this property; a continuous version of the Geometric, called the Exponential, is the other one. We have not yet deﬁned continuous RV’s or their expectation, but when we do the deﬁnition of the mgf for a continuous RV will be exactly the same.The resulting number of times a 1 is not rolled is represented by the random variable \ (X\), and the geometric distribution is the probability distribution of \ (X\). Visit Stack Exchange Apply it (if you do not remember the statement, check your lecture notes or Wikipedia) to your geometric random variable — you will need first to show the expectation is 2, and to compute the variance; and then .

Geometric Distribution

It makes use of the mean, which you’ve just derived. has the memoryless property if for all nonnegative.

Let X denote geometric random variable with probabili… - SolvedLib

Ω X x Pr ( X = x) By definition of geometric distribution : E(X) = ∑k∈ΩX kpk (1 − p) E ( X) = ∑ k ∈.From the definition of expectation : E(X) = ∑x∈ΩX x Pr(X = x) E ( X) = ∑ x ∈.Suppose a discrete random variable X has the following pmf P(X = k) = qkP; 0 k <1 The X is said to have geometric distribution with parameter P. NB: The main idea of this approach is to express the random variable X directly in terms of the random variable Y (which .If a random variable X follows a geometric distribution, then the probability of experiencing k failures before experiencing the first success can be found by the following formula: P . Its moment generating function is M X(t) = E[etX] At this point in the course we have only considered discrete RV’s. Geometric Distribution PMF. Lecture 8 : The Geometric Distribution.Geometric distribution is a type of discrete probability distribution that represents the probability of the number of successive failures before a success is obtained in a .The sum of two independent Negative Binomial random variable with identical failure rates, is a Negative Binomial Random Variable with the same failure rate and a stopping amount equal to the sum of their stopping amounts. There's a tricky issue with wording. Instructions: first calculate the probability P( min (X, Y) > k) and compare it to the parallel probability in (of?) a geometric random variable.

Probability with geometric random variables

The variance of a geometric random variable $X$ is: $\sigma^2=Var(X)=\dfrac{1-p}{p^2}$ Proof.2 Formulation 2. Hot Network Questions Does it mean that Robert is correcting Isador Rabi when he says ‘Canyons of New Mexico’? Remark Usually this is developed by replacing “having a child” by a Bernoulli experiment and having a girl by a “success” (PC).

PPT - Random Variable PowerPoint Presentation, free download - ID:7173

Stack Exchange Network. Let p ∈R be a real number such that 0 < p < 1 .

QVOC

Music