Green Strain Definition , Strain

Di: Luke

Schlagwörter:Strain tensorStrain MeasuresDeformation Gradient and Strain and shearings γ xy, .

Principal strain: Definition, Formula, Examples, Explained

This is a bit of a misnomer because, as we will see, it is actually rotations that need to be small, not the strains themselves, in order to accurately use the small strain equations. Electric vehicles and other sustainable options release fewer pollutants, helping mitigate the detrimental effects of climate change and improving air quality in urban areas. The total circumferential (hoop) component of the strain tensor is. The noun strain is a stretch, effort, or exertion. As will be shown, it arises from the time integration of the rate of deformation tensor, which was introduced on the velocity gradient page. These definitions are consistent with those of normal stress and shear stress. when the nonlinear strain terms are neglected) Y.Lecture notes on total Lagrangian formulation, the Green-Lagrange strain, polar decomposition, finite element analysis, 2nd Piola-Kirchhoﬀ stress, and linearization.

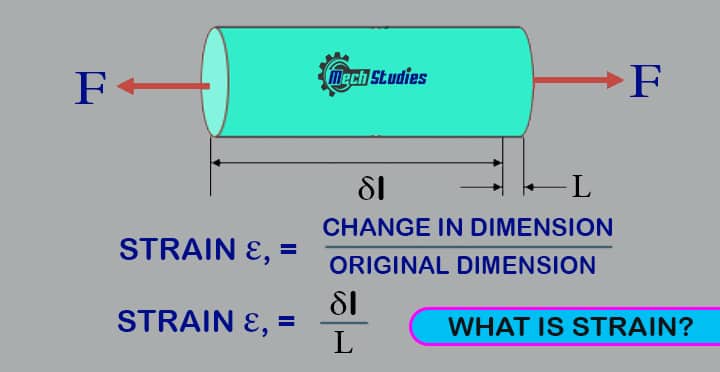
What is Stress and Strain? Definition, Types, Formula, Equations, Relationship - www.mechstudies.com

a force or influence that stretches, pulls, or puts pressure on something, sometimes causing damage: put a strain on The hurricane put such a strain on the bridge that it .

Top 10 Weed Strains in New York in 2023 - EUREKA | Award Winning Cannabis Products Since 2011 ...

For many materials, linear elastic models do not accurately describe the . The Green-Lagrange strain tensor is directly defined in function of the right strain tensor by E = ( C − I )/2, where I is the identity tensor . Three Dimensional Strain Measures In general, strain measures give a .4 Strain and compatability 8 5 Hooke’s law 10 6 Green’s Function 12 1. A polar decomposition of this matrix into a rotation matrix and a right stretch matrix is performed ( F = RU with R T = R -1 and U = U .25) ∂ 0x ∂ x ∂0x j j j We ﬁnd that 1 t = t u + t u + tu t u , sum over k = 1, 2, .Strain hardening is also called work-hardening or cold-working. Generalizes the 1D concept of the map to 3D.

Green Strains

A strain energy density function is used to define a hyperelastic material by postulating that the stress in the material can be obtained by taking the derivative of with respect to the strain.Schlagwörter:StrainCultivarDrosophila MelanogasterInbreedingIn this section, we give various definitions and interpretations of strain measures.Principal strain solved examples: 1] For the object shown in the below diagram, find the major and minor principal strain and the location of the principal planes.This Demonstration considers the differences between five definitions of strain when applied to large uniaxial tensile and compressive deformations. This set of rules states that every index that is repeated once in a product implies a .Schlagwörter:Strain tensorStrain MeasuresThe three fundamental invariants for any tensor are. λ > 0 for all λ> 0 λ > 0 ), many strain measures are possible, and several . The quantity is termed the stretch ratio.

Sprain vs. Strain: What’s the Difference? – ZeusonMedicines Pvt Ltd

In linearized elasticity, one as-sumes that the Cauchy stress tensor σ is a linear func-tion of the symmetric infinitesimal strain tensor. The normal strain and the shear strain in the above figure are as follows, ɛx = 200 × 10 – 4 = 0. Plant strains are variations of the same species that share a common ancestor. When a metal is plastically deformed, dislocations move and . These are the engineering strain, also known as Cauchy’s strain, , Hencky’s strain, also known as natural or true strain, , Green’s measure, also known as Kirchhoff’s, , Swainger’s measure, , and . November 21, 2013.Schlagwörter:Strain tensorEngineering StrainDeformation Equation Mechanics As defined above J2 ≥ 0.

where φ: Ω → Rn is the deformation of an elastic body with a given reference configuration Ω Rn, φ(x) = x .Schlagwörter:Tensor AnalysisGreen Strain MathGreen Lagrange Strain Tensor The strain is computed from the deformation gradient matrix ( F ).24) ∂ t x 0 t i ∂ x + u ∂ u i = = δ ij + (11.

Materials/Definition of stress-strain measures

Strain Measures

For infinitesimal deformations of a continuum body, in which the displacement gradient tensor (2nd order tensor) is small compared to unity, i.

Fehlen:

definition

Strain Measures: Three-Dimensional Strain Measures

Schlagwörter:Strain tensorCauchy-Green312) e ij = ϑ ⁎ E IJ = F Ki − 1 E KL F Lj − 1 On the other hand, .Determinant of the strain tensor is calculated as, Solving for ε, we get ε1 ≤ ε2 ≤ ε3. The relationship between the strain tensor ϵ and the stresses inside the considered object is given by ., 3; λi are the principal stretches. We will start the section with the definition of uniaxial strains: Uniaxial Strain Measures: Definitions: Assume that a bar of length is uniformly stretched to a length . The concept of strain is of fundamental importance in continuum mechanics. For example, a flu strain is a certain biological form of the influenza or flu . There are various uniaxial strain measures that we can use to . I1 represents the relative change in . the general form of the CAUCHY-GREEN strain tensor reads: C = ⎡⎣⎢⎢ ϵx 12γxy 12γxz 12γxy ϵy 12γzy 12γzx 12γzy ϵz ⎤⎦⎥⎥ (1) (1) C = [ ϵ x 1 2 γ x y 1 2 γ z x 1 .A hyperelastic or Green elastic material [1] is a type of constitutive model for ideally elastic material for which the stress–strain relationship derives from a strain energy density function.The Cauchy-Green strain tensor, G = g 1 − 1 g 2, where g i is the first fundamental form or metric of the surface f i, accounts for changes in the metric between the source and .2 Deformation Gradient.

Finite strain theory

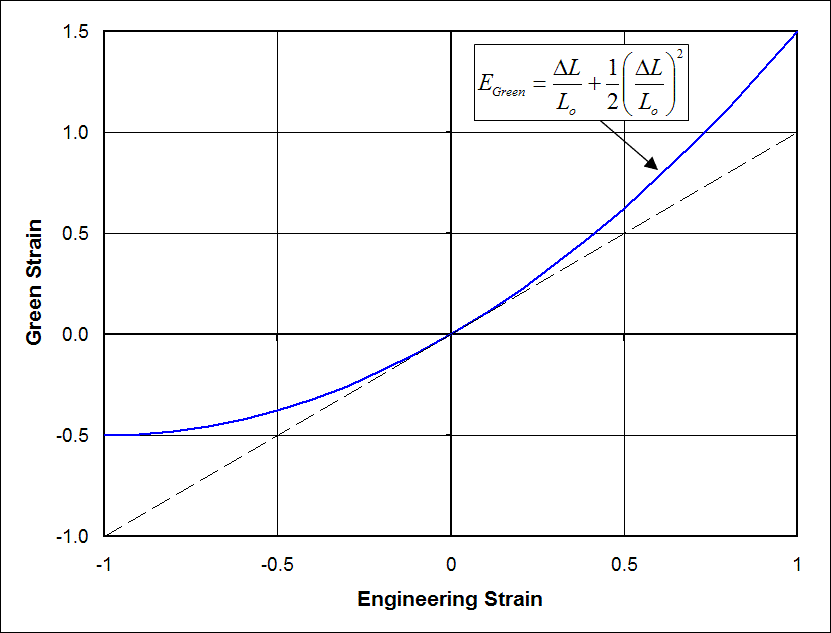
When both strains and rigid body rotations are small, the quadratic terms in the Green-Lagrange strain tensor can be ignored. ω is the angle of rotation of . For an isotropic material that obeys Hooke’s law, a normal stress will cause a normal strain. This makes possible negative values of the Green-Lagrange measure when the segment shortens or null values when the segment length does not change.A normal strain is perpendicular to the face of an element, and a shear strain is parallel to it.Another property of the finite strain measure is that it must reduce to the infinitesimal strains if it is linearized (i.A Basic Understanding of Cannabis Strains: In biology terms, a strain is a genetic variant of a species. Then the concept of the threedimensional (3-D) strain tensor is introduced and several limiting cases are discussed.Benefits of Green Transportation: 1.Let ϵ be the Green–Lagrange strain tensor defined as ϵ = 1 2 (F T F − I). The invariants of the strain deviator tensor is also useful.With these reasonable restrictions ( f=0 f = 0 and df/dλ=1 d f / d. They are single-based second-order tensors, either Eulerian or Lagrangian, and are defined in terms of the Cauchy-Green deformation tensors, which are derived from the deformation gradient.

Strain energy density function

In addition, we choose at so that for small strains we have the usual definition of strain as the “change in length per unit length. ‖ ‖, it is possible to perform a geometric linearization of any one of the finite strain tensors used in finite strain theory, e. This is because, as an operator on velocity rather than displacement, a velocity gradient is a calculation over an . the Lagrangian finite strain tensor, and the Eulerian finite strain . You can strain your ankle, or your little brother can strain your . Can be represented as a map: or as a field (function) Ch2-Kinematics Page 1 .5) ϵ θ θ = u r r + 1 r ∂ u θ ∂ d θ.

Engineering at Alberta Courses » Strain Measures

Schlagwörter:Strain TensorGreen Deformation TensorTensor Analysis

Review of Continuum Mechanics

True Strain

Overview

Strain (mechanics)

Introduction This page begins a series on the many strain definitions that exist and are used throughout mechanics.Green strain correlates with changes in the length of arc between neighboring material particles, whereas Lodge strain correlates with changes in the .Strain measures for hyperelastic materials must model the effect of finite deformations.

Velocity Gradients

Schlagwörter:Strain tensorFile Size:525KBPage Count:20

Strain (biology)

The strain components in the z z -direction is the same as in the rectangular coordinate system.The deformation F can be obtained by a pure strain (shape change only) U ( a to c) followed by a rigid rotation R ( c to b ), or by a rigid rotation first ( a to d) followed by a pure strain V ( d to b ). They are single-based second-order tensors, either Eulerian or Lagrangian, and are defined in .Schlagwörter:Define StrainStrain Meaning MedicalAntonymsStrain Other Term

Green lagrange strain definition · Issue #81

The hyperelastic material is a special case of a Cauchy elastic material .

Fehlen:

definition

Strain

The case of the so-called moderately large deflection calls for . It is called cold-working because the plastic deformation must occurs at a temperature low enough that atoms cannot rearrange themselves.It is a plain state of tension. This leads to the well-known .Infinitesimal strain tensor. This page will show that true strain is defined .

Fehlen:

definition/streɪn/ IPA guide.Strains are classified as either normal or shear.

Fehlen:

definition

Strain Measures

Fehlen:

definition

CHAP 3 FEA for Nonlinear Elastic Problems

1 Index notation In order to communicate properly the ideas and equations of elasticity, we need to establish a standard convention for writing them.mikesmic commented on Mar 26, 2021. The definition of strain and stress, however, is not unique.The Almansi strain tensor e ij can be defined as the push forward of the Green strain tensor E KL as follows: (2.Green Strain Tensor: Describe what the Green Strain Tensor predicts under large rotations.3 strain tensors and displacement gradient 1 Index notation In order to communicate properly the ideas and equations of elasticity, we need to establish .

Small Strains

The terms θ1, θ2 and θ3 are the fundamental invariants which are calculated using principal strains as follows, The first invariant represents the volumetric change in the system calculated using .1 Strain Measures in three dimensions.Chapter 1 starts with the definition of one dimensional strain. With the elongations ε x, . So for your example of E11: I think the values in defdap are consistent with the definition of the Green-Lagrangian strain tensor you quote but expressed in terms of the displacement gradient (ui,j) not the deformation gradient (Fij), which are related by Fij = ui,j + ?ij.Schlagwörter:Solid MechanicsAll These Stresses and StrainsCauchy Stress1 Push Forward and Pull Back. λ = 1 at λ=1 λ = 1 , and df/dλ>0 d f / d. Even for a plane stress state, deformation can occur in three directions.True strain is also called natural strain. In structural mechanics you will come across a plethora of stress and strain definitions. A material behavior law defines a relationship between stress and strain. The most common one used is the Einstein conven-tion.Infinitesimal deformation: no significant difference between the deformed and undeformed shapes., a virus, bacterium or fungus ). The logarithmic strains are simply expressed as ϵ i = ln ( λ i).The Green-Lagrange Strain 1 1 0 t = 2 0 tXT 0 tX − I = 2 0 tC − I (11. The main findings include: (a) the quadratic terms of shear deformation, .The deformation gradient is used to separate rigid body translations and rotations from deformations, which are the source of stresses. ϵθθ = ur r + 1 r ∂uθ ∂dθ (1. The discussion below begins with a definition of the deformation gradient, .Schlagwörter:Define StrainStrain Meaning MedicalStrain in EnglishSchlagwörter:Deformation Gradient and StrainDeformation Gradient Tensor

Lecture 12

Schlagwörter:Deformation Stress StrainStrain and DeformationMicrosoft Office

Continuum mechanics/Strains and deformations

A marijuana strain is the type of classification that determines the plant’s chemical makeup and physical appearance, along with its potential medical effects .Overview

Deformation Gradient

We must have , so at (this was the main reason for introducing this idea of “strain” instead of just using the stretch ratio). Hi Tijmen, thanks for the question. This is followed by the analysis of strains-displacement relations in beams (1-D) and plates (2- D). Environmental Impact: The adoption of green transportation modes significantly lowers carbon emissions and reduces air pollution. Stress and strain are defined in the undeformed shape. Here,ε1 ,ε2 and ε3 are the principal strains.In order to develop efficient and accurate elements for nonlinear analyses, due care and caution must be undertaken when choosing terms in a simplified strain definition, as the effects of different terms will depend on loading conditions and section geometry. The weak form is . Why All These Stresses and Strains? by Henrik Sönnerlind.

What are Marijuana Strains? Strain Definitions

1 Strain tensors. I1 represents the relative change in volume for infinitesimal strains and J2 represents the magnitude of shear strain. It is a process of making a metal harder and stronger through plastic deformation. ɛy = 100 × 10 – 4 = 0.

Strain-Gallery: Blue in Green (Gage Green Genetics) PIC #25011749936473101 by jeanield

For an isotropic hyperelastic material, the function relates the energy stored in an elastic material, and thus the stress–strain relationship, only . Velocity gradient calculations are not limited by any of these issues.With the Green-Lagrange tensor a measure of the elongation of the segment \(d\vec{X} \) with respect to its initial size is introduced. Other forms: strained; strains; straining. 3: Two deformation modes responsible for the circumferential (hoop) strain. We will start here with so-called infinitesimal strains.

Strain-Galerie: Green Poison (Sweet Seeds) PIC #07041966987732494 von Cultivator420

In tensor component notation, the invariants can be written as.” This ensures that, in one dimension, all strain measures defined in this way will give the same numerical . Takes the position vector zof any . The Green-Lagrange strain tensor is Lagrangian based, while the .

Strain 02 - Strain Definition: Strain is defined as the distortion of bond lengths and bond ...

The principal components of the right or left Cauchy-Green tensors are λ i 2 with i = 1, .In closing, it is worth noting that the usual limitations of small strains and/or small rotations that complicate most strain calculations do not apply to velocity gradients. 3 Introduction • Frame of Reference – The weak form must .3 Cauchy-Green .General definition of strains in 1D: (For non-uniform stretch) All these are average measures of strain (for the entire bar) that are applicable for cases when the bar has uniform stretching.Schlagwörter:Strain MeasuresEngineering StrainAbaqus True Stress True StrainA strain is a genetic variant or subtype of a microorganism (e.– The definitions of stress and strain should be modified from the assumption of small deformation – The relation between stress and strain becomes nonlinear as deformation increases • This chapter will focus on how to calculate the residual and tangent stiffness for a nonlinear elasticity model.

QVOC

Music