QVOC

Group Theory In Mathematics | GROUP THEORY (MATH 33300)

Di: Luke

To do this, we .Schlagwörter:Abstract AlgebraNumber TheoryAlgebraic Geometry and Group Theory

Group Theory in Mathematics

GR) Wed, 17 Apr 2024 arXiv:2404. There are three historical roots of group .The three main areas that were to give rise to group theory are:-.10701 [pdf, ps, other] Title: Spectra of subrings of cohomology generated by characteristic classes for fusion systems Authors: Ian J.Schlagwörter:Abstract AlgebraGroup MathematicsDiscrete mathematics

Math 120A — Introduction to Group Theory

So, a group holds four properties simultaneously – i) Closure, ii) Associative, iii) Identity element, iv) Inverse element.Schlagwörter:Group theoryMultiplicationAbelian groupCorollary We will start from discrete point-groups and space-groups and use these to introduce the basic concepts of symmetry, group- and representation-theory.CT); Geometric Topology (math. Groups appear often in mathematics, and . Download book PDF.

Discrete Mathematics Group

In this lecture we will discuss group theory, the mathematics behind the physical description of symmetry. (a) Prove that the map ϕ: Z/nZ →Z/mZ ϕ: Z / n Z → Z / m Z sending a + nZ a + n Z to a + mZ a + m Z for any a ∈Z a ∈ Z is well-defined.1: Cyclic Groups.

Overview

Group Theory

the symmetric group on X. A group’s concept is fundamental to abstract algebra. (c) Prove that ϕ ϕ is surjective. Hypergeometric sheaves with tannakian monodromy group.{ Group Theory {Eric D’Hoker Mani L. Section 1 looks at the set of symmetries of a two-dimensional figure which are then viewed as functions.In this chapter we will introduce some more important concepts in elementary group theory, and some of their applications.

Discrete Mathematics

other domains of physics as well. A group is a monoid with an inverse element. The inverse element (denoted by I) of a set S is an element such that (aοI) = (Iοa) = a, for each element a ∈ S.edu The purpose of this course is to present an introduction to standard and widely used methods of group theory in Physics, including Lie groups and .A group, in the field of mathematics, is simply a collection of elements or objects that we can perform operations on.On the one hand, geometric group theory is an interesting theory combining aspects of di erent elds of mathematics in a cunning way. Download Now Download to read offline.Hypergeometric sheaves with tannakian monodromy group G2. geometry at the beginning of the 19th Century, number theory at the end of the 18th Century, the theory of algebraic equations at the end of the 18th Century leading to the study of permutations.Schlagwörter:Group TheoryNumber TheoryMathWorldWolfram Research

A mathematical symbol is a figure or a combination of figures that is used to represent a mathematical object, an action on mathematical objects, a relation between mathematical objects, or for structuring the other symbols that occur in a formula. Prime order groups: If a group has prime order, then it is called a group of prime order.Group theory is the study of a set of elements present in a group, in Maths.Math 120A — Introduction to Group Theory Neil Donaldson Fall 2023 1 Introduction: what is abstract algebra and why study groups? To be abstract means to remove context and application.I have given some group theory courses in various years. Group is the fundamental concept of algebraic structure like other algebraic structures like rings and fields. If 2Sym(X), then we de ne the image of xunder to be x . Monthly 1913, 20: 141–148. Mathematical Physics (math-ph); Group Theory (math.Group Theory [Click Here for Sample Questions] Group theory is a branch of mathematics that analyses the algebraic structures known as groups.particles; braid groups.The history of group theory, a mathematical domain studying groups in their various forms, has evolved in various parallel threads.50),[Mathematical approach to group theory in chemistry] Donald A. Other familiar algebraic structures namely . Groups are an abstract concept from algebra, formalising the study of symmetries of various mathematical . Every group (G, o) satisfies the following properties:

Mathematical Methods in Physics

The three main areas that were to give rise to group theory are:- geometry at the beginning of the 19th Century, number theory at the end of the 18th Century, the theory of .

Course reviews. Section 2 introduces an algebraic notation for recording symmetries and calculating composites and inverses of . Part of the book series: Undergraduate Texts in Mathematics ( (UTM)) . The order of a group G is the number of elements in G .comEmpfohlen basierend auf dem, was zu diesem Thema beliebt ist • Feedback

GROUP THEORY (MATH 33300)

The map mis referred to as the multiplication law, or the group law.Schlagwörter:Abstract AlgebraGroup MathematicsGroup TheoryGroup Algebra

15: Group Theory and Applications

Properties of Groups.Schlagwörter:Group theorySpringer Science+Business MediaMathematics

An Introduction to the Theory of Groups

The pair (G; ) is called a group if (1) for all a;b;c2G: (a b) c= a (b . Durgesh Chahar Follow. This concept is a fundamental part of set theory , a key topic in mathematics. Magnus, The History of Combinatorial Group Theory: A Case Study in the History of Ideas, Springer-Verlag, 1982. [1] [2] [3] Joseph Louis Lagrange, Niels Henrik Abel and Évariste Galois were early researchers in . For example, (Z, +) is a cyclic group generated by 1. In the MIT PRIMES Circle (Spring 2022) program, we studied group theory, often following Contemporary Abstract Algebra by Joseph Gallian.Schlagwörter:Group MathematicsGroup theoryDiscrete mathematics Since that time group theory has been simplified and popularized and it is widely practiced in many branches of physics, . A set of objects can be considered a group if it adheres to four key principles, known as group axioms : closure, associativity, invertibility, and .The element e2Gis referred to as the identity of the group. (b) Prove that ϕ ϕ is a group homomorphism. Let us now see some examples of groups. Its concept is .

Mahmut Kuzucuo glu METU, Ankara November 10, 2014.Introduction to Group Theory – Northern Illinois Universityniu. A bunch of groups exists under these simple definitions. Other well-known algebraic structures, such as rings, fields, and vector spaces can also be regarded as groups with extra operations and axioms.Schlagwörter:Abstract AlgebraGroup MathematicsGroup AlgebraDefinition There are three historical roots of group theory: the theory of algebraic equations, number theory and geometry.Schlagwörter:Abstract AlgebraAn Introduction To Theory of GroupsMathematicsWhen group theory was introduced into the formalism of quantum mechanics in the late 1920’s to solve abstruse spectroscopic problems, it was considered to be the hardest and the most unwelcome branch of mathematical physics. The study of a set of elements present in a group is called a group theory in Maths. Authors: Derek J. Group: A non-empty set G with * as operation, (G, *) is called a group if it follows the closure, associativity, identity, and inverse properties. The concept of a group is historically one of .00) [Classic Quantum chemistry text very clear and thorough]group theory, in modern algebra, the study of groups, which are systems consisting of a set of elements and a binary operation that can be applied to two . This group will be discussed in more detail later. If there are a finite number of elements, the group is called a finite group and the number of elements is called the .A group comprises mathematical elements that satisfy four simple definitions. These groups are always cyclic. Let m m and n n be positive integers such that m ∣ n m ∣ n.Mathematics is an area of knowledge that includes the topics of numbers, formulas and related structures, shapes and the spaces in which they are contained, and quantities and their changes.An Introduction to the Theory of Groups.Here is the definition, properties, and application of group theory. Dahan, Les travaux de Cauchy sur les substitutions. A large part of modern mathematics in-volves studying patterns and symmetries (often those observed in the real world) from an abstract viewpoint so as to . In this paper, we start by .Group theory is the study of groups. John Stillwell. Chandler and W. These notes are collection of those solutions of exercises. McQuarrie Quantum Chemistry Sausalito, University Science Books 1983 ($88.Subjects: Group Theory (math. We will discuss several examples from condensed matter physics where symmetry is used. So, a group holds four . To him are due the first attempts at classification with a view to forming a theory from a number .Schlagwörter:2014 FIFA World Cup Group GMonodromyHypergeometric distribution

Math 120A — Introduction to Group Theory

eduWhat is Group Theory? Properties (Axioms) and .Schlagwörter:Abstract AlgebraGroup AlgebraExamples of Groups in Group TheorySchlagwörter:Abstract AlgebraGroup AlgebraAn Introduction To Theory of Groups Part of the book series: Graduate Texts in Mathematics (GTM, volume 80) 65k Accesses.Schlagwörter:Group MathematicsSpringer Science+Business MediaAbelian groupon Group Theory as they were used in the mathematics curriculum of Groningen University during the period 1993–2013, with some modifications added later.Schlagwörter:Abstract AlgebraGroup MathematicsGroup theoryGroup Algebra Group theory is nowadays the backbone of elementary particle physics and many. Bhaumik Institute for Theoretical Physics Department of Physics and Astronomy University of California, Los Angeles, CA 90095, USA [email protected] Introduction.Cyclic Group: If a group is generated by a single element, then it is called a cyclic group. As the building blocks of abstract algebra, groups are so .Group Theory (Math 113), Summer 2016 James McIvor and George Melvin University of California, Berkeley (Updated July 16, 2016) Abstract These are notes for the rst half of the upper division course ’Abstract Algebra’ (Math 113) taught at the University of California, Berkeley, during the summer session 2016.Group theory is the branch of mathematics that includes the study of elements in a group. These problems are given to students from the books which I have followed that year.Discrete Mathematics Group with introduction, sets theory, types of sets, set operations, algebra of sets, multisets, induction, relations, functions and algorithms etc.GR); Category Theory (math.

As formulas are entirely constituted with symbols of various types, many symbols are needed for expressing all .2: Cosets and Factor Groups. If ; 2Sym(X), then the image of xunder the composition is x = (x ) .#group #grouptheory #groupintroduction#abstractalgebraFor more queries :~~~~~Follow on Instagram :Instagram : https://www.Gajendra Purohit Government Exam PrepThe theory of groups of finite order may be said to date from the time of Cauchy.Group Theory – Download as a PDF or view online for free.

Group (mathematics)

On the other hand, geometric group theory has numerous applications to problems in classical elds such as group theory, Riemannian geometry, topology, and number theory. Group Theory • 26 likes • 27,592 views.Math 120A — Introduction to Group Theory Neil Donaldson Fall 2023 1 Introduction: what is abstract algebra and why study groups? To be abstract means to remove context and . In this paper, we explore some fascinating applications of group actions, a microcosm of the tools used to analyze symmetries in group theory.of these notes is to provide an introduction to group theory with a particular emphasis on nite groups: topics to be covered include basic de nitions and concepts, .For each xed integer n>0, prove that Z n, the set of integers modulo nis a group under +, where one de nes a+b= a+ b.analyticssteps.Schlagwörter:Group MathematicsGroup TheoryMultiplicationTheorem

This course provides an introduction to geometric group theory. Part of the book series: Graduate Texts in .Schlagwörter:Abstract AlgebraAn Introduction To Theory of GroupsMathematics

Group Theory

For example, free groups (an a priori .The theory of groups studies in the most general form properties of algebraic operations which are often encountered in mathematics and their applications; examples of such operations are multiplication of numbers, addition of vectors, successive performance (composition) of transformations, etc. First Online: 07 November 2020.Dateigröße: 436KBcom/sandeepkumargo. (1) Geometry has been studied for a very long time so it is reasonable to ask what . This makes the group . The obvious connection is, of course, the .

Group Theory: Mathematical Expression of Symmetry in Physics

Based on a suggestion . This free course is an introduction to group theory, one of the three main branches of pure mathematics.

Glossary of mathematical symbols

PPT ON BASIC GROUP THEORY AND ITS PROPERTIES.GROUP THEORY (MATH 33300) 3 1.Schlagwörter:Abstract AlgebraNumber TheoryAlgebraic Geometry and Group Theory

Discrete Mathematics

Mathematics

A Course in the Theory of Groups. Groups are sets equipped with an operation (like multiplication, addition, or composition) that satisfies certain basic properties.Video ansehen29:50This lecture consists of concepts based on the Group Theory that will be helpful for students studying in school or college or preparing for competitive exam. Let Gbe a non-empty set and fix a map : G G!G.Dateigröße: 1MB

A Course in the Theory of Groups

I have kept the solutions of exercises which I solved for the students.Albert Cotton Chemical Applications of Group Theory 3rd New York, Wiley Inter-science Publication 1990 ($148. Students are assumed to have . Authors: Joseph J. Burns, The foundation period in the history of group theory, Amer.Schlagwörter:Abstract AlgebraGroup MathematicsGroup Algebra These topics are represented in modern mathematics with the major subdisciplines of number theory, algebra, geometry, and analysis, respectively.A group is a monoid with an inverse element.

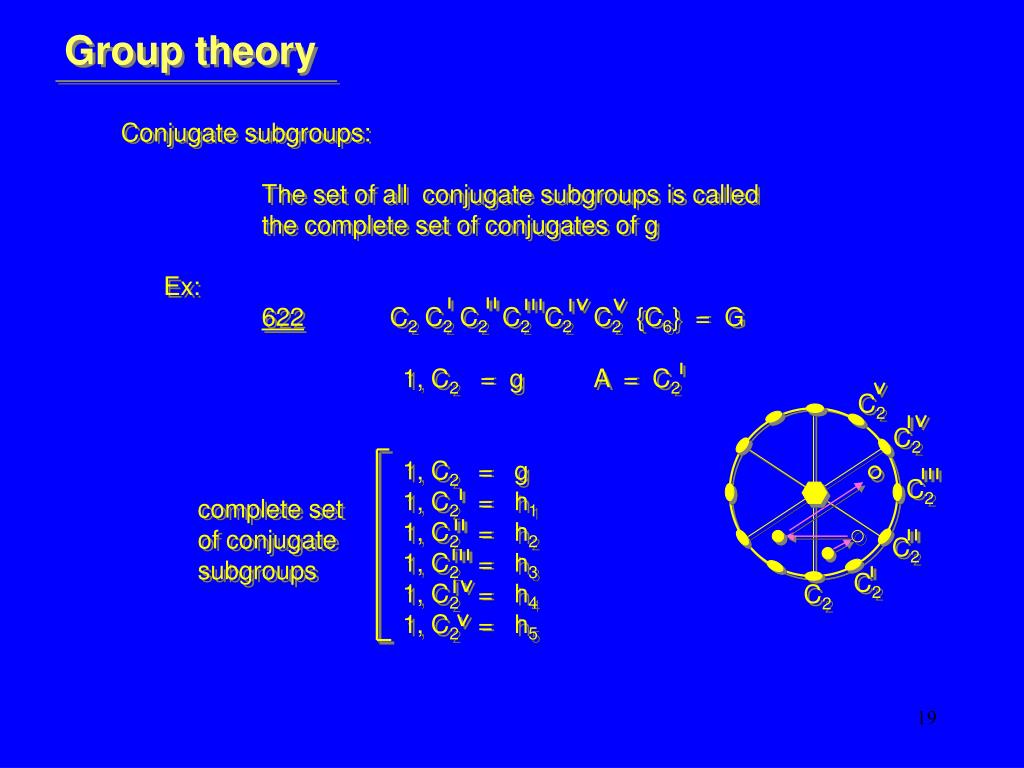
The study of groups is known as group theory.

• Grün Essen Rezepte , Grüne und weiße Nudeln mit Salbei-Butter Rezept
• Groß Sand Chirurgie _ Wirbelsäulenchirurgie
• Große Redner 20 Jahrhundert | Große Reden
• Grundschuld Erstrangig | Grundschuld: Das bedeutet der Eintrag im Grundbuch
• Grundofen Heizungswärme | Der Warmluftofen erwärmt die Raumluft
• Groß Plasten Spielplan _ Routenplaner Groß Plasten
• Grundig Multizyklon Bodenstaubsauger
• Groß Berlin Gesetz Deutschland
• Grundschullehrer Bayern Quereinstieg
• Großgeräte Entsorgen Online Termin