QVOC

Music

Implizite Funktionen Ableiten Tabelle

Di: Luke

Kategorien: Version 5. Dauer: 45 Minuten. In einer Kurvendiskussion kannst du durch Ableiten insbesondere herausfinden, wo die .Verständliche Erklärung der arctan Ableitungsregel. Diese Formel ist zentral, um die Steigung der Tangente an der . Im Fall \ (n=1\) wissen wir, dass eine stetig differenzierbare Funktion f ( x) mit \ (f‘ (x)\ne 0\) eine stetig differenzierbare . Verweise: Lösungsskizze. In der folgenden Abbildung 6 sind beispielhaft drei Stammfunktionen für C 1 = 1, C 2 = 2, C 3 = – 2 dargestellt.

Implizite Ableitung: Zusammenhang Mehrdimensionale Analysis

Implizite Funktionen Durch die Bedingung F(x;y) = C ; C 2 Rwird eine bestimmte Teilmenge des R2 festgelegt, z. Sie wird auch oft dafür benutzt, um die Ableitung von Funktionen, die zwar explizit gegeben sind, in dieser Form aber schwierig abzuleiten sind, zu berechnen. Implizit gegebene Funktionen einfach erklärt Viele Analysis-Themen Üben für Implizit gegebene Funktionen mit Videos, interaktiven Übungen & Lösungen. Betrachten wir die Situation zunächst bei Funktionen zweier Veränderlicher (Skizze).

Ableitungsrechner • Mit Rechenweg!

In der Tabelle siehst du schon mal alle Ableitungsregeln .deAbleitungsrechnerrechner-kostenlos. Anmerkung: Siehe auch den Befehl Ableitung. Der Zusammenhang zwischen zw ei V ar iab len x und y kann gegeben w erden durch eine explizite Funktion: y = f(x) Beispiel: y = x2. f‘ (x) gibt uns dann für jeden x-Wert die Steigung in diesem Punkt.Diese wahrheitsfunktionale objektsprachliche Implikation wird unter anderem materiale Implikation, Subjunktion oder (zunehmend) Konditional genannt. Weitere Videos sind im Tutorial verlinkt. für Donnerstag, 17. Ableitung einer Funktion mehrerer Veränderlicher wird mittels partieller Ableitungen auf den Fall eindimensionaler Funktionen zurückgeführt. Also ist eine stetige Familie stetiger Funktionen eine Menge von Funktionen, die alle stetig sind und von einem Parameter . was genau ist dieses dx/dy und warum steht es hinter y^3 und nicht hinter x^3. Sie drückt die hinreichende Bedingung aus, das heißt, sie behauptet keinerlei kausalen oder sonstigen inhaltlichen Zusammenhang zwischen und .

Ableitung Rechner

Satz von der impliziten Funktion | Herleitung | Beispiel x^2 y^2 - 1 = 0 - YouTube

In diesem Text schauen wir uns zwei Beispiele und eine .Dann erhalten wir für jedes feste xeine Funktion f x(y)=x +y, die dann nur noch von yabhängt, da xja fest ist. Am Graphen siehst du deshalb, dass die Funktion an x = 0 fällt: Ableitung einer Funktion. diese Auflösung durch. Handbuch (offiziell) Manual (official) Befehle. Was eine Ableitung ist, wissen wir bereits aus der Schule: Steigungsdreieck und so weiter.

Implizite Funktionen

) oder die Ableitung einer impliziten Funktion zusammen mit einer Anzeige der angewendeten Regeln.Ableitung Implizite GleichungWenn noch spezielle Fragen sind: https://www. Lösungsvorschlag. Mithilfe des Satzes über inverse Funktionen ergeben sich Kriterien für die Eindeutigkeit (Satz über implizite Funktionen).

Tabellen für Ableitungsregeln und besondere Ableitungen. | Nachhilfe mathe, Mathe abitur ...

Zu bilden sei die Ableitung der .Mehrdimensionales Ableiten. Zu bilden sei die Ableitung der Funktion f(x, y) = 3y4 + 2×2 + 10x – 5y = 0 .

Funktionen (mehrdimensionale)

Implizite Funktionen, Totale Ableitung und Jacobi-Matrix. Exponential- und Logarithmusableitungen.

Tabelle der Ableitungen

Extremalstellen unter Nebenbedingungen stellen eine wichtige Anwendung impliziter Funktionen dar.

Wichtige Stammfunktionen: Tabelle & Beispiele I StudySmarter

Die Ableitung nach den Variablen, nach denen aufgel¨ost werden soll, muss invertierbar sein. Beispiel: f_a (x) = a\cdot x^3+3a. Ableitungen trigonometrischer Funktionen. Um eine implizite Funktion zu differenzieren benutzen wir die verallgemeinerte Kettenregel. Ableitungen von Funktionen mit mehreren Variablen (partielle Ableitungen), implizite Ableitungen .Tabelle der gängisten Ableitungen. Beispiel: Baumwachstum.

Mehrdimensionales Ableiten

deEmpfohlen auf der Grundlage der beliebten • Feedback

Implizite Ableitungen Rechner

4 Wenn man sich nicht genau erinnert, welche Bedingungen in dem Satz zu impliziten Funktionen stehen, kann man sich das wie folgt merken.1 Auflösen von Gleichungen.Ableiten einer impliziten Funktion. Juli 2014 Woche 12, Implizite Funktionen Bemerkung 12. Mit anderen Ableitungsregeln kannst du beispielsweise die Exponentialfunktion und die Logarithmusfunktion ableiten. Direkte Ableitungen. grad f = (y2 + 4xz, 2xy z2, 2yz + 2×2)t. Wenn spezielle Fragen auftauchen: https://www. Schon im Altertum wurde diskutiert, .In diesem Video besprechen wir den Satz über implizite Funktionen und betrachten dazu zwei Übungsaufgaben.Implizites Differenzieren / Implizite Ableitung – Welt der BWLwelt-der-bwl.

Implizite Funktionen

Ableitung Cobb Douglas Funktion.den man eine implizite Funktion in zwei oder mehr Variablen (das heißt eine Funktion, in der nicht eine Variable in Abhängigkeit von der anderen explizit gegeben ist) nach einer . f1 f = f f1= id idist die Einheitsfunktion oder identische Funktion :id (x) = x f1(f(x)) = f1(y ) = xundf(f1(y )) = .y = 6 – x (als explizite Funktion) 2x + 2y = 12 (als gleichwertige implizite Funktion) Beide Funktionen stellen dasselbe – nur anders – dar (was man leicht überprüfen kann, wenn . Beispiel: ImpliziteAbleitung[x^2 + y^2, y, x] berechnet -\frac {x} {y}. Danach gilt: F_x (x,y)\cdot x’+F_y (x,y)y‘ F x(x,y) ⋅x′ + F y(x,y)y′ =F_x .Die implizite Differentiation (auch implizite Ableitung) ist eine Möglichkeit impliziete Funktionen mit Hilfe der mehrdimensionalen Differentialrechnung abzuleiten. Aufgabe 1: Zweite Ableitung einer Auflösung.Man kann sehr leicht die Ableitung der Funktion y f(x, g+(x)) ≡ 0 ist, folgt mit der Kettenregel: = g+(x) berechnen. Definition: Ableitung der Funktion an der Stelle wird als Grenzwert des Verhältnisses des . Aus der Tabelle der Grund- oder Stammintegrale lassen sich die Stammfunktionen direkt ablesen.zu impliziten Funktionen. Ableitung (2) Mathematik Klasse 10. Bilde die erste Ableitung folgender Funktionen.Die Tabelle der Ableitungen — notwendig für die Berechnung der Ableitung, die wiederum ist die wichtigste Operation in der differenzierten Berechnung.1 (¨uber implizite Funktionen) Sei Ω ⊂ Rm × Rk offen und f ∈ C1(Ω,Rk).Die Ableitung bezeichnest du mit f‘ (x). Dabei k˜onnen wir oBdA C = 0 annehmen, da wir stets zur Betrachtung von Fe(x;y) = F(x;y)¡C ub˜ ergehen k˜onnen.de Playlists zu allen Mathe-Themen findet ihr auf der Startseite . Gegeben sei die implizite Funktion und ein Punkt .c2006 und implizite Funktion Mathematische Methoden VII Implizite Funktionen 2 / 8. Es kommen in der .Wir haben bereits im Kap. Partielle Ableitung. f! Df, y 7! x = f1(y ) heißt inverse Funktion zuf, falls.

Implizite Differentiation

Die Ableitung von arctan \ ( x \) wird definiert als 1 1 + x 2. Deshalb unter Verwendung der abgeleiteten Tabelle können Sie schnell alle Aufgaben zu meistern. Um nun die partielle Ableitung im Punkt zu berechnen, nutze: Prüfe, ob gilt. Beispiel: \large {f (x) = \frac {3x^2 \cdot (2x+5)} {3x+1}} 2.Implizite Ableitung. Auflösen nach y′ : . f\left (x\right)=2x+3 f (x) = 2x +3. A x + B y = 0, A ∈ ℝm × m, B ∈ ℝm × d, x ∈ ℝm, y ∈ ℝd.

Ableiten • Funktionen ableiten, graphisches Ableiten

Die erste Ableitung der Auflösung einer solchen Funktion nach y ist nach dem Satz aus der VL gegeben durch: (∂xf)(x, g(x))Zwei grundlegende Sätze der reellen Analysis mehrerer Veränderlicher: der Satz von der impliziten Funktion und der Satz von der Umkehrabbildung. Banachscher Fixpunktsatz. Ist f(x0,y0) = z0 und Dyf(x0,y0) ∈ L(Rk,Rk) invertierbar, so gibt es offene Umgebungen U von . Sei f : R2 → R, (x, y) 7→f(x, y) = 0 ein implizite Funktion. f‘ (0) zum Beispiel ist dann -3, also kleiner 0.

Implizite Ableitung

(i) Auflösbarkeit: Gradient.implizite\:ableitung\:\frac{dy}{dx},\:(x-y)^2=x+y-1 ; implizite\:ableitung\:\frac{dy}{dx},\:x^3+y^3=4 ; . durch die Bedingung x ¡ y = 4 . Partielle Ableitungen kannst du von Funktionen bilden, die von mehreren Veränderlichen abhängen.Aufgabe: Implizites Ableiten. Im Spezialfall k = 1 bedeutet das. Diese Funktion ist dann stetig in y. Die Cobb-Douglas Funktion wird partiell . Sie kann oft auch benutzt werden, um die Ableitung von .

2 Implizite Funktionen

Der Ableitungsrechner kann die erste, zweite, .Überprüfen Sie mit Hilfe des Satzes über implizite Funktionen, ob sich die Gleichung \ (F (x,y,z)=0\) im Punkt (0, 3, 1) lokal nach x und y oder nach x und z oder nach y und z auflösen lässt und führen Sie ggf.Rechner löst die Ableitung einer Funktion f (x, y (x).Implizite Funktionen. 23 das Thema implizite Funktionen angesprochen: In der Praxis sind Funktionen oft nicht durch explizite Angabe der .

Implizites Differenzieren / Implizite Ableitung

Berechnet die implizite Ableitung des angegebenen Ausdrucks.Um die Ableitung einer Funktion zu berechnen , verwendest du einige Ableitungsregeln , zum Beispiel für Potenzfunktionen x p: Beispiel: f(x) = x 2 + 3x → f'(x) = 2x + 3. Sie ist durch x = A −1 y definiert. F ( x) = ∫ 3 x d x = 3 x ln ( 3) + C.Implizite Differentiation: Aufgaben 1, 2 2-1 Ma 1 – Lubov Vassilevskaya Aufgabe 1: Bestimmen Sie durch implizites und explizites Differenzieren die Ableitung folgender Funktionen a) xy− x 2 y=−3, b) ey−x 2 = 1 x Aufgabe 2: Bestimmen Sie durch implizites Differenzieren die Ableitung folgender Funktionen in den Punkten P Abbildung 6: Exponentialfunktion und Stammfunktionen. Die implizite Differentiation (auch implizite Ableitung) ist eine Möglichkeit, eine Funktion, die nicht explizit durch einen Term, sondern nur implizit durch eine Gleichung gegeben ist (auch implizite Kurve), mit Hilfe der mehrdimensionalen Differentialrechnung abzuleiten. Wenn man f(x;y) = 0 auch als y= Y(x) schreiben kann, wobei Y eine di erenzierbare Funktion ist, dann gilt f(x;Y(x)) = 0:09 von Carla Zensen.

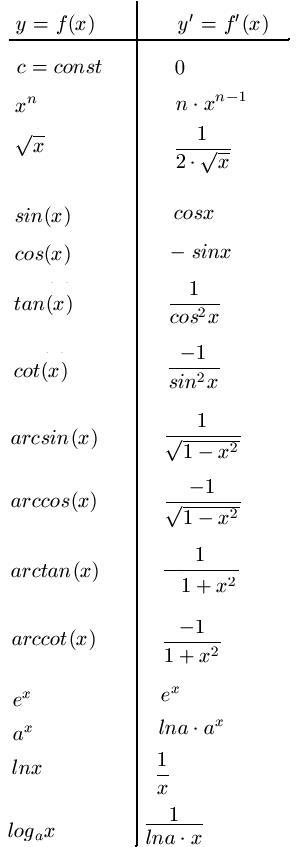
Ableitung: Tabelle / Formelsammlung

Mehr noch, diese Familie von Funktionen hängt auch ste-tig von x ab. Die Ableitung nach den Variablen, nach denen aufgel ̈ost werden soll, muss ∂f invertierbar sein. Um wirklich mit der Cobb Douglas Funktion rechnen zu können, ist es wichtig zu verstehen wie die Ableitung funktioniert.

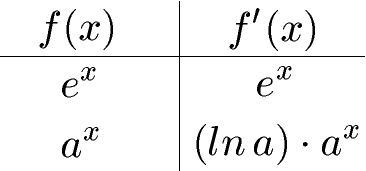
Tabelle Ableitung / Ableitungstabelle

Ein lineares Gleichungssystem. 12y4 ⋅ dy dx + 4x + 10 – 5 ⋅ dy dx = 0 .Lösungen zu impliziten Funktionen – TUMph.Die implizite Form kann komplizierte Flächen im R3 darstellen, die ex-plizite Form „kann“ nur solche Flächen, die jedem (x,y) . Beispiel: Die Ableitung von f (x) = x3 – 3x ist f‘ (x) = 3×2 – 3. Gib einfach die Funktion ein, um die Lösung, Schritte und den Graphen zu sehen. Auch innerhalb des Lagrange-Ansatzes wird die Cobb Douglas Nutzenfunktion oft verwendet, dafür ist die Ableitung ein wichtiger Zwischenschritt.Implizite Funktionen ergeben sich als Auflösungen von allgemeinen Gleichungssystemen. A x = y, A ∈ ℝm × m , x, y ∈ ℝm, hat bei vorgegebenem y genau dann eine eindeutige Lösung x, wenn A invertierbar ist. ∂y (x0, y0) 6= 0.Implizite Differentiation. Wir haben auch schon Ableitungsregeln kennen gelernt, mit deren Hilfe wir für eine Funktion f (x) die Ableitung f‘ (x) bestimmen können. Satz über Umkehrabbildungen (lokal) Taylorpolynome (mehrdimensional) Theorie: Partielle Ableitungen. existier t nicht implizite Funktion: F (x,y) = 0 Beispiel: y x2= 0 x2+ y21 = 0 Fra g en: W ann kann man eine implizite Funktion . x^3+y^3 = 12 3x^2+3y^2 dx/dy = 0. f\left (x\right)=x^2+3 f (x) = x2 + 3.Ist eine Gleichung in impliziter Darstellung f(x, y) gegeben, läßt sich die Ableitung bilden, indem man alle Terme ableitet (Kettenregel beachten !) . Allgemeiner können wir das System., fünfte Ableitung berechnen.deImplizite Funktionen – Mathepediamathepedia.

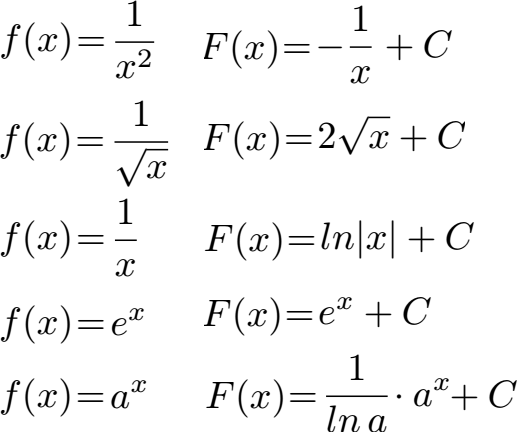
Grundintegrale / Tabelle Integrale

de Playlists zu allen Mathe-Themen findet ihr auf der Startseite unter:.0:00 – 17:30 Erklärung17:30 – 19:20 Wie denken Math. warum steht es hinter y 3 und nicht hinter x 3. f = xy2 yz2 + 2zx2, −.Kostenlos Ableitungsrechner – leite Funktionen ab inklusive aller Teilschritte. Der Ausdruck F(x;y) = 0 kann auch so interpretiert werden, dass eine . Im Spezialfall k = 1 bedeutet das ∂f ∂y(x0,y0) 6= 0. Ist eine Gleichung in impliziter Darstellung f(x, y) gegeben, läßt sich die Ableitung bilden, indem man alle Terme ableitet (Kettenregel beachten !) . ableitungen; implizite-funktion ; implizit; differenzieren; Gefragt 29 Jan von Mathematikerrr. Eine Partielle Ableitung, ist die Ableitung nach einer Varibalen von . 0 = (x, g+(x)) · 1 + (x, g+(x)) · g0 +(x), ∂x ∂y.Ableitung bestimmen bei einer impliziten Gleichung.deEmpfohlen auf der Grundlage der beliebten • Feedback

Implizite Differentiation