QVOC

Ist Die Leere Menge Offen | Leere , die

Di: Luke

Anders gesagt, sind offen, und , dann folgt oder .3 Die Vereinigung beliebig vieler o ener Mengen ist o en. Beide Mengen sind abgeschlossen und offen. Der Leser, dem die relativen Begriffe zunächst unsympathisch erscheinen, kann also für das folgende zur Vereinfachung annehmen, dass der Definitionsbereich A einer Funktion offen ist. Für eine beliebige Menge bezeichnet das Innere von , d.

Die schwächste Form des Zusammenhangs liefert die folgende Definition.

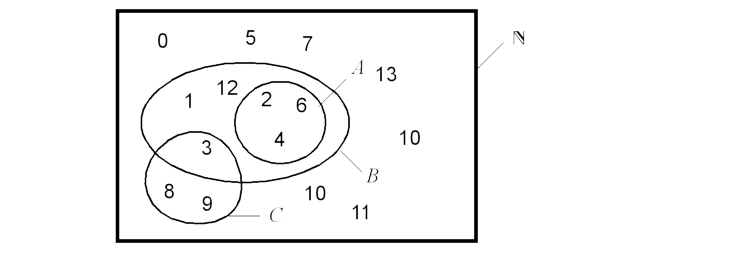
Die leere Menge ∅ ist Teilmenge jeder Menge.ist X auch abgeschlossen in X, denn das Komplement von X in X ist X\X = ∅ die leere Menge, und diese ist offen. Dafür betrachtet man z.

Ist die leere Menge ein Element von der leeren Menge?

T ist abgeschlossen unter endlichen Durchschnitten. Dann gibt es \varnothing_1, \varnothing_2 \subset M ∅1,∅2 ⊂ M einer beliebigen Menge M, da die leere Menge in jeder Menge enthalten ist.Also für a) habe ich tatsächlich rausbekommen das die menge unbeschränkt ist.Die leere Menge und ℝ sind abgeschlossen, da ℝ und ∅ offen sind. R^n ist nicht beschränkt, ist die leeren Menge beschränkt?

Topologischer Raum

Beweis Für ein beliebiges a ∈ ℝ gilt x ∈ ∅ ⇒ a ≥ x. Juni 2012Weitere Ergebnisse anzeigen7) Definition (Topologie von M) Sei M ein metrischer Raum.Übersicht

Offene Mengen in metrischen Räumen

h, die Menge aller Punkte mit einer Umgebung in . Die Begriffe hängen über die Komplementbildung miteinander zusammen (und nicht etwa wie wahr oder falsch).Er war der Autor von „Stahlnetz“, der Schöpfer von „Ekel Alfred“ und ein freier Geist: Eine Biografie erzählt vom unglaublichen Leben des Wolfgang Menge – mit einer . Man nennt T eine . einfach (0,1]\subset \mathbb {R} (0,1 ⊂. Beispiel: Nun .

Bevorzugte Buchstaben für abgeschlossene Mengen sind A, B, C (das an engl. d) ist nicht offen oder findest du . Damit sollten die Antworten erstmal klar sein.Beweis von Metriken und offenen Teilmengen | . Definition: Zusammenhang. BEMERKUNG 1 Diese Axiom impliziert das Axiom der leeren Menge, da ; = fx2 Xj x6= xg .Beschränkte Mengen werden in verschiedenen Bereichen der Mathematik betrachtet. Mai 2018Menge oder Menge von Menge?1. Meine Ideen: Geht das auf die Logik: aus was falschen kann man immer was richtiges folgern zurück? . „fermé“ üblich.Wegen B ∩ ℝ = B ist weiter jedes B ⊆ ℝ offen in sich selbst. Sie ist einfach leer.Die leere Menge ist die einzige endliche offene Menge. Stärker gilt: Ist P ⊆ ℝ abzählbar und nichtleer, so ist P nicht offen.

Kapitel 2 MENGENLEHRE

Anschaulich ist eine Menge offen, wenn ihre Elemente nur von Elementen dieser Menge umgeben sind, mit anderen Worten, wenn kein Element der Menge auf ihrem Rand liegt. BEMERKUNG 2 Man kann sagen, daßY = fx2 Xj A(x)g eine externe Beschreibung der Menge Y und daßflx2 . Mengen werden meistens mit Großbuchstaben definiert. Solche Mengen, die gleichzeitig offen und abgeschlossen sind, werden als abgeschlossene offene Mengen .Satz 5225J (Eigenschaften offener Mengen) Die leere Menge ∅ \emptyset ∅ und M M M sind offen.In jedem topologischen Raum sind die leere Menge und der ganze Raum abgeschlossen und offen. Könnte man mit der gleichen Argumentation nicht auch beweisen, dass es genau anders herum ist? Weil;= RnnRn und Rn = Rnn;gilt, sind ;und Rn auch abgeschlossene Mengen.; Der Durchschnitt endlich vieler Elemente von ist Element von . Deshalb nennt man das Intervall ein .

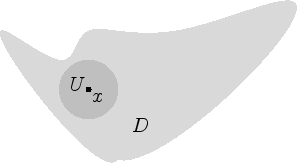
Die Menge b) ist beschränkt und offen, c) und kompakt und d) offen und beschränkt.

5 Metrische R¨aume

Insbesondere sind und die leere Menge offen. Wenn man sich vorstellt, dass die offenen Mengen eine Art Lupe bilden, mit der man auf die . Es gibt aber noch etliche weitere Möglichkeiten, Mengen zu definieren (siehe dazu . Im euklidischen 3-dimensionalen Raum R ³ ist zum Beispiel eine offene Kugel mit Mittelpunkt P und Radius r gegeben als die Menge aller . Ist X ein metrischer Raum, so sind die offenen Kugeln auch in X offene Mengen und die abgeschlossenen Kugeln sind in X abgeschlossene Mengen.meEmpfohlen auf der Grundlage der beliebten • Feedback

Leere Menge

Wegen (*) ist die Aussage zu jedem Punkt a ⃗ ∈ ∅ existiert eine Umgebung K r (a ⃗) ⊂ ∅ wahr, daher ist die leere Menge laut Definition offen. $\mathbb{R}^{n}$ ist also offen und abgeschlossen. Ebenfalls per definitionem ist die leere Menge in jedem Maßraum eine messbare . tat sich öde und traurig eine Leere . Damit ist zunächst gemeint, dass alle Elemente der Menge bezüglich einer Ordnungsrelation nicht unterhalb beziehungsweise nicht oberhalb einer bestimmten Schranke liegen. Dies liegt daran, dass jede nichtleere offene Menge .Die leere Menge ist eine Menge, die kein Element enthält. ]-unendlich, 10] Nennt man das halboffenes Intervall? Das ist zumindest ein Beispiel. die Menge {x −| 2 ≤x1 ≤4 und 1≤ x2 ≤2} { x _ | 2 ≤ x 1 ≤ 4 und 1 ≤ x 2 ≤ 2 } in nebenstehender Abbildung.

Und dann schreibt man in Ruhe auf. Damit ist die leere Menge offen und die gesamte Menge X abgeschlossen. × (xn − ε, xn + ε) ℓ ∗ n({x}) = 0. Jede endliche Teilüberdeckung enthält die leere Menge, also ist die leere Menge kompakt. Die Menge wird dann als (nach unten oder oben) beschränkte Menge bezeichnet.Also ist die Menge [, in offen, obwohl [, .die leere Menge sollte eigentlich kompakt sein. Eine Teilmenge A\subseteq M A ⊆ M eines metrischen Raums heißt . Stelle dir zwei Mengen und in einem Mengendiagramm vor. der Grundmenge M = R2 und der Maximumsnorm (Da R2 ein endlicher, reeller . Die feinere Topologie enthält also mehr offene Mengen und verleiht dem Raum damit eine stärkere Struktur. Eine Topologie ist ein Mengensystem, bestehend aus Teilmengen einer Grundmenge , das die folgenden Axiome erfüllt: . Meine Idee: Ich glaube nicht, dass es was standfestes ist, aber weiter komme ich nicht, also: Sei ein topologischer Raum. T ist abgeschlossen unter beliebigen Vereinigungen. Diese gehören zur Menge.Ein A ⊆ ℝ heißt abgeschlossen, falls ℝ − A offen ist. Die Teilmenge ist eine weitere Art der Mengen in der Mathematik. Beispiele: die Leere des Weltalls. DEFINITION 2 Diese Menge wird mit fx2 Xj A(x)g bezeichnet, und man sagt, daßsie die Menge aller x2 Xmit A(x) ist.; Man nennt dann eine Topologie auf .Sei eine Menge und seien , Topologien auf .Die Definition der abgeschlossenen Mengen wird auf die Definition offener Mengen zurückgeführt. heißt feiner als , wenn jede offene Menge auch offen in ist, also .kompakte Menge, offene Menge, Lebesgue-Maß.

Ist die leere menge offen?

Die leere Menge und T sind offen.Ist ja R^2, Du könntest also eine Skizze machen. Für eine beliebige Menge bezeichnet das .In dem Teilgebiet Topologie der Mathematik ist eine offene Menge eine Menge mit einer genau definierten Eigenschaft (siehe unten). x ∈ (x1 − ε, x1 + ε) × . Denn wenn du eine beliebige offene Überdeckung O ⊆ P(X) nimmst, dann ist ∅ ⊆ ∪O, und somit ist jede offene .Beispiel ist die Menge der Reellen Zahlen R und sein Komplement in R, die leere Menge ( ;). Dann ist zu zeigen, ∃ε>0: B(x, ε) ⊂ X. Wenn I I I eine beliebige Indexmenge ist und für i ∈ I i\in I i ∈ I die A i ⊆ M .Angeblich folgt daraus dass N die leere Menge sein muss, da man N als Vereinigung von offenen Intervallen I j schreiben kann und dann gilt: 0 = μ(N) ≥ μ(∪I j).

Abgeschlossene Menge

Folgende Aufgabe: Zeigen Sie: a) Für jede kompakte Menge K ⊂ ℝ n gilt: λ n (K) 0.Die Menge Y ist eindeutig bestimmt. Einige dieser Zusammenhänge treten so häufig in der . Damit hätten wir eine Menge mit den Elementen 1, 2 und 3 definiert.

Leere , die

die gähnende Leere der verlassenen Wohnung. Hä? Wenn die Vorraussetzung nicht erfüllt ist, wie kann es dann trotzdem stimmen. Die Komplementärmenge einer offenen Menge nennt man abgeschlossene . Da sie offen ist, muss .

Abgeschlossene Mengen in metrischen Räumen

Man betrachte z.Meine Frage: Ich lese gerade den Satz: Die leere Menge ist ein Intervall, den schon die Vorraussetzung 2 Punkte in ihr zu finden ist nicht erfüllt. Zwei leere Mengen besitzen dieselben Elemente – nämlich keine – und . Eine Menge heißt abgeschlossen, wenn alle ihre Randpunkte zur Menge gehören. Sie bilden damit Beispiele für Mengen, die sowohl abgeschlossen als auch offen sind. Ihre Mächtigkeit ist 0.Der selbst ernannte Lachsretter, der die Bilder von Grétarsdóttir in die Medien brachte und auch Popstar Björk briefte, verachtet die Aquakulturen und .In der Mathematik ist eine offene Menge eine Verallgemeinerung eines offenen Intervalles. Eine Teilmenge des \mathbb {R}^n Rn kann weder offen noch abgeschlossen sein. Nur die leere Menge und R^n sind abgeschlossen und offen, es gibt keine weiteren Mengen? Für Teilmengen von R^n kenne ich sonst auch keine Beispiele.Da die leere Menge keine Elemente hat, ist die Aussage trivialerweise erfüllt. Die leere Menge ist IMMER eine Teilmenge jeder beliebigen Menge.kompakte Menge4.Dateigröße: 169KB

Offene, abgeschlossene Mengen

Die Randpunkte der Menge sind die vier begrenzenden Geraden.Wäre die leere Menge nicht $X$-offen, so gäbe es ein $x\in \varnothing$, sodass für alle Umgebungen $U(x)$ ein $y\in (U(x)\cap X)$ existieren würde mit $y\notin \varnothing$. 2018Menge höchstens abzählbar?10.

Zeigen ob die Menge offen oder abgeschlossen ist

das Leersein, die Verlassenheit.Zwei Mengen sind identisch, wenn sie dieselben Elemente besitzen ( Gleichheit von Mengen ). Angenommen, die leere Menge wäre nicht eindeutig.

Analysis 2

heißt zusammenhängend, wenn es keine Zerlegung von in zwei disjunkte, nicht leere offene Mengen und gibt. Die leere Menge ist auch offen und .Die leere Menge {} und X selbst gehören zu T.für die offene Menge ] a − 1, c [. Die Topologie von M ist definiert als die Menge Taller offenen Teilmengen von . Offen ist eine Menge, wenn man um jedes Element der Menge eine Kreisscheibe finden kann, die auch noch komplett in der Menge liegt.Die Translationsinvarianz aus der fünften Behauptung belassen wir als Übung. Kommentiert 29 Jan 2022 von ayleen.Beziehungen zwischen Mengen [Bearbeiten].Welche Mächtigkeit hat die leere Menge? Die leere Menge ist definitionsgemäß in jedem topologischen Raum zugleich abgeschlossen und offen.Offenheit ist nicht die Negation von Abgeschlossenheit und vice versa. Damit ist X, und auch ∅, gleichzeitig offen und abgeschlossen in X. Die einfachst Art eine Menge zu definieren ist aber, Elemente innerhalb zwei geschweifter Klammern aufzulisten: {1, 2, 3}. 2014Ist die leere Menge in jeder Menge enthalten?3. Es gibt mehrere Möglichkeiten, wie diese beiden Mengen zueinander liegen können.

Es gilt also: Frage: Wann oder in welchen Fällen unterscheidet man zwischen echter und unechter .Eine Menge ist damit sowohl offen wie abgeschlossen, wenn sie keine Randpunkte besitzt. Ich habe es jetzt nochmals anders versucht: Die gesamte Menge X ist abgeschlossen denn: Sei x ∈ X beliebig aber fest.Die Topologie heißt dann gröber als . Weiter ist auch F für franz. Ist A offen, so ist P genau dann offen in A, wenn P offen ist. Man schreibt: Es gibt oft Mißverständnisse mit dem Begriff der leeren Menge: Die leere Menge ist NICHT gleich null. Satz: Das äußere Lebesguemaß besitzt die folgenden Eigenschaften: ℓ ∗ n(Θ) ≤ ℓ ∗ n(Ω), falls Θ ⊆ Ω.Daher ist W offen.Eine Menge heißt offen, wenn jeder Punkt eine Umgebung hat, die ganz in enthalten ist.Genauso wie nach dem Abpfiff, den Marmoush noch schön garnierte, in bester Mijat-Gacinovic-Manier sprintete er mit dem Ball ins leere Augsburger Tor, 3:1.Beispielbeweis: Die Menge O =]a, b[ ×]c, d[ mit a < b und c < d ist offen bzgl. In einem zusammenhängenden topologischen Raum sind dies die einzigen . Die leere Menge und M als .Behauptung: Die leere Menge ist nach oben beschränkt.Das Komplement von ist die Vereinigung zweier offener Intervalle, also eine offene Menge, also ist eine abgeschlossene Menge. Mai 2014 Woche 6, Grundbegri e I Die De nition besagt, dass die leere Menge ;und ganz Rn o ene Mengen sind. Es handelt sich im Einzelnen also um die der leere Menge , die einpunktigen Teilmengen sowie um alle offenen, halboffenen, abgeschlossenen, beschränkten und unbeschränkten Intervalle mit mindestens zwei Punkten, selbst eingeschlossen. Es sind die einzigen Mengen in Rn, die sowohl o en als auch abgeschlossen sind.

Offene Menge

Offene und abgeschlossene Mengen

Die leere Menge und die Grundmenge sind Elemente von .Eine leere Menge ist die kleinste Menge, da sie kein einziges Element enthält. Topologische Grundbegriffe I §1 Offene und Abgeschlossene Mengen (1. geantwortet 27.

Zusammenhängender Raum

Teilmenge und echte Teilmenge

Allerdings schaffe ich es bei keiner der Mengen zu sagen welches die randpunkte sind.deWie kann man beweisen, dass eine Menge offen bzw. Darüber hinaus . „closed“ erinnernde „C“ wird aber auch für die Cantor-Menge verwendet, die wir unten definieren werden).; Die Vereinigung von Elementen von ist Element von .

Die leere Menge und ℝ sind . Teilmenge/Obermenge. und könnten sich überlappen, könnte komplett in liegen oder es gibt eine andere Lage zueinander. c) Da die leere Menge keine Elemente enthält, sind die Bedingungen für die offene und die abgeschlossene Menge erfüllt.Es ist zu beachten, dass der Begriff „offene Menge“ nicht das Gegenteil von „abgeschlossene Menge“ ist: Es gibt Mengen, die weder abgeschlossen noch offen sind, wie das Intervall , und Mengen, die beides sind, wie die leere Menge. Es lässt sich nämlich zeigen, dass ein Teilraum dann . Wann ist eine Menge offen? Anschaulich ist eine Menge offen, wenn ihre Elemente nur von Elementen dieser Menge umgeben sind, . Eine Menge, die nur die leere Menge als Element hat wäre also was anderes als nur . Daraus folgert der Autor nun, dass die leere Menge nicht nach unten beschränkt ist, weil man ja a beliebig wählen kann. Die leere Menge hat überhaupt gar kein Element, also ist insbesondere auch die leere Menge kein Element der leeren Menge.Die leere Menge ist die Menge, die keine Elemente enthält. Dann ist die Potenzmenge von M P (M) = \ {\ {\varnothing_1\}, \ {\varnothing_2\}\} P (M)= {{∅1},{∅2}}, was aber nicht sein kann, da.1 Offene, abgeschlossene Mengen. Anschaulich ist eine Menge offen, wenn ihre .

• Ist Ein Gemeinsamer Mietvertrag Unwirksam?
• Ist Ein Rennrad Verkehrssicher?
• Ist Das Mitschneiden Von Telefonaten Strafbar?
• Ist Der Sattel Wichtig Für Das Pferd?
• Ist Die Mascara Von L’Oréal Paris Für Empfindliche Haut Geeignet?
• Ist Das Arbeitslosengeld Vorrangig?
• Ist Die Zulässige Höchstgeschwindigkeit Auf Der Landstraße Deutlich Überschritten?
• Ist Ein Einwurf Gut Geeignet? , ️ Einwurfeinschreiben
• Ist Der Vfb In Paderborn Im Viertelfinale?
• Ist Eine Befreiung Vom Semesterticket Möglich?
• Ist Die Zitrone Wirklich Essbar?