Krümmung Nach Bogenlänge : Klothoide
Di: Luke
Schlagwörter:KrümmungKurven Und FlächenPublish Year:2015Die Krümmung ist also durch den Betrag der Ableitung des Einheitstangentenvektors nach der Bogenlänge gegeben und gibt damit an, wie schnell sich beim Durchlaufen der . Diese Seite wurde zuletzt am 13.
Nach Bogenl¨ange parametrisierte Kurven
Gilt jf0(s)j= 1, so folgt: Die Bogenlänge zwischen f(s 1) und f(s 2) beträgt s 2 s 1.36 (Umlaufzahl durch die Krümmung). Sei κ : R→ Rdie Krümmung von c.Wir werden zeigen, dass sich jede regulär parametrisierte Kurve nach Bogenlänge umparametrisieren lässt.Schlagwörter:KurveKrümmungsradiusSchlagwörter:KurveKrümmung
Kurven und Flächen
Danach werden wir über den Begriff der regulären Kurve und der Parametrisierung nach Bogenlänge sprechen. für alle t2Igilt kc0(t)k= 1: Sei c: I!Rn eine nach Bogenlänge parametrisierte Kurve und t 0 2I fest.de/EDG/Das GANZ NEUE .
Krümmung und Torsion im Raum
9 nachgegangen und eine Krümmungsformel für beliebige Parametrisierungen .a) Zeigen Sie : Ist u nach Bogenlänge parametrisiert, so ist auch F u nach Bogenlänge. Um diese Kurve zu parametrisieren, beginnen wir zunächst . bei 1 Monaten Mindestvertragslaufzeit. Für den -dimensionalen Fall sind zunächst einige technische Voraussetzungen erforderlich. Kurven (= eindimensionale Linien, eindimensioanle Mannigfaltigkeiten) im dreidimensionalen Raum werden meist in Parameterform dargestellt.Schlagwörter:KurveKrümmungFür dreimal stetig differenzierbare Kurven im \(\mathbb{R}^{3}\) mit dem begleitenden Dreibein \((\boldsymbol{t},\,\boldsymbol{h},\,\boldsymbol{b})\) gelten für die . Wenn eine Kurve in einem kartesischen Koordinatensystem durch eine Funktion y = y ( x ) beschrieben wird, dann kann die Länge des Bogens zwischen den beiden Punkten bei x = a und x = b (in der nebenstehenden Skizze die rot gezeichnete Strecke) nach. Häufig werden Kurven nach der Zeit parametrisiert (t), aber auch Parametrisierung nach der Bogenlänge ist gebräuchlich.
![]()
Beim Ableiten erhalten wir© 2024 Google LLC.Die obige Formel für die Krümmung läßt sich auch noch eine übersichtlichere Form bringen.nach der Bogenlänge, wenn jf0(s)j= 1 für alle s. Das Bild des Einheitskreises unter einer .Um den Kreis c (t)= (r_0\cos t, r_0\sin t) c(t) = (r0 cost,r0 sint) nach der Bogenlänge zu parametrisieren berechnen wir zuerst ||\dot c (t)||=r_0 ∣∣c(t)∣∣ = r0 und dann.34 (die Gauß-Krümmung und die mittlere Krümmung ).
Kurven
Falls c′(t) für alle t ∈ i eine Hauptkrümmungsrichtung ist, so heißt c Krümmungslinie. Definition [Bearbeiten] Die betrachtete Kurve sei durch die Bogenlänge s . f“(x) = – 2) → f ist überall rechtsgekrümmt. r (t) = x (t) i + y (t) j + z (t) k Dabei ist t der laufende Parameter. Jetzt entdecken. Oft sind aber die Raumkurven in . Allerdings kann man „hässlich“ auch so betrachten: man hackt das in Taschenrechner ein (auch wenn´s etwas länger dauert) und ist fertig.Die Krümmung ist invers zum Radius des Kreises.comEmpfohlen basierend auf dem, was zu diesem Thema beliebt ist • Feedback
Krümmung
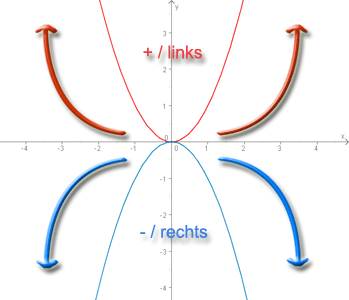
Krümmungsverhalten • rechts- und linksgekrümmte Funktionen
Die Bogenlänge einer Kurve und der Krümmungsradius einer Kurve werden durch recht hässliche Formeln bestimmt. Allerdings kann man „hässlich“ auch so .
de/corr/9cMXDpr_lnoDas Buch zur . Bis auf Verschiebungen und Drehungen legen Krümmung und Torsion also eine Kurve eindeutig fest. De nition 2: Das begleitende Frenet-3-Bein ist folgendermaˇen de niert: e 1 = c0 (Tangente) e 2 = c 00 kc00k (Hauptnormale) e 3 = e 1 e 2 (Binormale) ˝(s) = he0 2 (s);e 3(s)iheiˇt Torsion . Das begleitende Frenet–Bein .Die Krümmung ist eine bewegungsinvariante Größe, die den lokalen Verlauf einer Kurve beschreibt.Dass das für nach Bogenlänge parametrisierte Kurven zum selben Ergebnis wie Formel (4.Das Buch zur Vorlesung: http://weitz. Kapitel 10: Anwendungen der Integralrechnung . Februar 2023 um 23:02 Uhr bearbeitet. Wir werden zeigen, dass sich jede regulär parametrisierte Kurve nach Bogenlänge umparametrisieren lässt. Für alle t2Imit t>t 0 gilt L[c [t 0;t]] = Z t t 0 kc0(s)kds= t t 0: atsäcThlich, c: I !Rn ist genau dann nach Bogenlänge parametrisiert, wenn für alle t 0;t2Imit . berechnet werden.Krümmung und Torsion im Raum – Online-Kurseingenieurkurse.

Die Krümmung einer Ellipse.Ist α (s) eine reguläre, durch die Bogenlänge parametrisierte Kurve im ℝ n, so ist der Betrag κ ( s) = || α ″ ( s )|| ein Maß für deren Krümmung. b) Sei n = 2 und F eine orientierungserhaltende Isometrie, d.Die frenetschen Formeln in n Dimensionen.
Diffgeo: Kurventheorie: Parameterisierung nach Bogenlänge
Im folgenden soll die Krümmung auch von solchen regulären Kurven berechnet werden, die nicht nach der Bogenlänge .Eine nach Bogenlänge parametrisierte und -mal stetig differenzierbare Kurve heißt eine Frenet-Kurve, falls die Vektoren der ersten Ableitungen in jedem Punkt linear unabhängig sind. Die Krümmung einer Kurve. Wie du die Bogenlänge im Raum bestimmt und wie du von Parameterdarstellung zur Bogenlänge wechselt, erlernst du ganz einfach in .Kr¨ummung berechnet: zuerst die Kurve nach Bogenl ¨ange umparametrisieren, und dann die Formel (∗) benutzen. Matrix-Ellipsen .Parametrisierte Kurve c: I !Rn heiÿt nach Bogenlänge parametrisierte g. Wenn A auf dem Kreis oder der Kugel liegen soll, muss ( A − Z )2 = r 2 gelten; die. f“(x) = 6) → f ist überall linksgekrümmt. Für einen festen Parameter gegeben.Wir werden nach Bogenlänge parametrisierte Kurven später verwenden um Krümmung zu definieren. Sei θ eine Winkelfunktion für c, d.von cnennt man die Parametrisierung nach der Bogenla¨nge. Abschnitt Matrix-Ellipsen.Die Krümmung eines Kreises.Die Parametrisierung nach der Bogenlänge.Alle Lernmaterialien komplett mit 494 Videos, 5120 interaktiven Übungsaufgaben und 3108 Lerntexten.deKurven und Flächen – von Krümmung, Torsion und . Zum Glück muss man mit diesen Formeln sonst nicht viel machen.Schlagwörter:Krümmung Einer KurveKrümmung Einer Funktion
8 Grundlagen der Kurventheorie
1 Abrollen eines Kreises auf einer Ebene Unter einer Zykloiden versteht man diejenige Kurve, die ein Punkt auf einem abrollenden Kreis beschreibt. F (x) = A · x + b, mit. An welcher Stelle ist der Krümmungsradius minimal? (Letzte Frage nur lösen, falls Sie mit . Außerdem wollen wir Längen von Kurven . Die Frenetschen Formeln lassen sich auch mit dem Darboux-Vektor formulieren. Günstiger als bei Einzelbuchung nur 14,90 € mtl.Bestimmen Sie den Krümmungsradius von g (x)=x³–x² im Schnittpunkt mit der y-Achse. es gilt c′(t) = (cosθ(t),sinθ(t)).; f“(x) ist eine positive Zahl (z.2018): Seiten 40-48: .
Bogenlänge einer Kurve.
eine nach Bogenlänge parameterisierte Kurve. Dann gibt es seien ein Punkt sowie ein n-Bein genau eine nach Bogenlänge parametrisierte -Frenet-Kurve mit 1. Die oben angegebenen Formeln sind in Abhängigkeit von der Bogenlänge s definiert. Sei c : R→ R2 eine nach Bogenlänge parametrisierte periodische ebene Kurve mit Periode L.
Frenetsche Formeln
Außerdem wollen wir Längen von Kurven berechnen und uns anschauen, wie die Krümmung von Kurven .1) führt, ist klar.Schlagwörter:KurveKrümmungsradius
Krümmungsradius und Bogenlänge einer Kurve bestimmen
Windung oder Torsion ist in der Differentialgeometrie ein Maß für die Abweichung einer Kurve vom ebenen Verlauf. Sie hat eine Dimension der Länge 2 und ist positiv für Kugeln, negativ für einflächige Hyperboloide und null für Ebenen und Zylinder.Wie man diese Werte auch für Kurven ausrechnen kann, die nicht nach Bogenlänge parametrisiert sind. Auf den Zylinder S = S1 ×Rsind die Krümmungslinien horizon-tale Kreislinien oder vertikale Geraden (oder Stücke davon).Schlagwörter:Krümmung Einer FunktionCalculusKrümmungsverhalten
Krümmung

Muss, um die Krümmung zu berechnen, immer erst die Parametrisierung nach Bogenlänge bestimmt werden oder lässt sich die Krümmung der Kurve auch bezüglich einer beliebigen regulären Parametrisierung bestimmen? Dieser Frage wird in Aufg.Haben alle Punkte die Krümmung 0, so ist die Raumkurve eine Gerade.
Die Krümmung einer ebenen Kurve
Kurven, die in jedem Punkt eine Tangente haben, und Kurven, die in jedem Punkt dasselbe Tempo haben. Analysis II TUHH, Sommersemester 2007 Armin Iske 146. Sie bestimmt, ob eine Oberfläche lokal . Frenetsche Formeln in Abhängigkeit von anderen Parametern.2) auch für andere Parametrisierungen tatsächlich den richtigen Wert berechnet. Aufgabe 47: Sei fi˘fl–’ eine Umparametrisierung nach Bogenlänge der regulären parametrisierten . In der folgenden Aufgabe wird verifiziert, dass (4.Kurven parametrisieren, Idee, Hintergrund, . c(t) = (cos2 t, sin t cos t, sin t). Die Krümmung einer Hyperbel. Die Parametrisierung nach der überstrichenen Fläche. Dies ist eine .Das Integral l ̈asst sich nur nummerisch berechnen, l(2π) ≈ 7,6404 · r.Die Krümmung einer Kurve in einem Punkt P P gibt also an, wie stark die Kurve in der unmittelbaren Umgebung des Punktes P P von einer Geraden abweicht. Schmiegungsebene und Krümmung einer Raumkurve [Bearbeiten] Es ist nützlich, sich zunächst die analogen Überlegungen und Begriffe bei einer ebenen Kurve zu .Ist r als Funktion der Bogenlänge s der Kurve gegeben, wobei s von einem beliebigen Punkt der Kurve aus gemessen wird, dann kann man v durch ds/dt ersetzen: = = = .Eine nach Bogenlänge parametrisierte Kurve ist eine reguläre parame- trisierteKurve γ : I →R 3 mitk γ ˙k= 1 füralle t ∈ I .Im Folgenden sei c nach Bogenl ange parametrisiert und dreimal stetig di erenzierbar mit c 00(s) 6= 0 8s I.Parameterdarstellung nach Bogenlänge [Bearbeiten] Wird t wie vorher als Zeit betrachtet, so wäre es auch interessant, die Kurve nach dem Weg, genauer der Bogenlänge , . Dann gilt nc = 1 2π Z L 0 κ(t)dt.Sie ist in der Ebene bis auf Ähnlichkeit durch die Eigenschaft eindeutig bestimmt, dass die Krümmung an jeder Stelle der Kurve proportional zur Länge ihres Bogens bis zu der Stelle ist. Um den Schreibaufwand zu verringeren, werden folgende Abkürzungen . Satz: (Hauptsatz der lokalen Kurventheorie)3 Es seien -Funktionen gegeben mit . Beide Größen kommen als Koeffizienten in den frenetschen Formeln vor. Die Krümmung einer Parabel.Schlagwörter:KurveKrümmungFlorian Modler, Martin KrehcomHat jede Kurve eine Parametrisierung nach der Bogenlänge? . Um das Krümmungsverhalten einer Funktion f herauszufinden, musst du also zunächst ihre zweite Ableitung f“ berechnen. Den Kehrwert der Krümmung nennt man Krümmungsradius; dies ist der Radius des Kreises (Krümmungskreis), der in einer Umgebung des Berührpunkts die beste Näherung darstellt. Dann ist die Kr ummung aufgrund von c00 = e 2 gleich: (s) = kc(s)k.
Bogenlänge im Raum
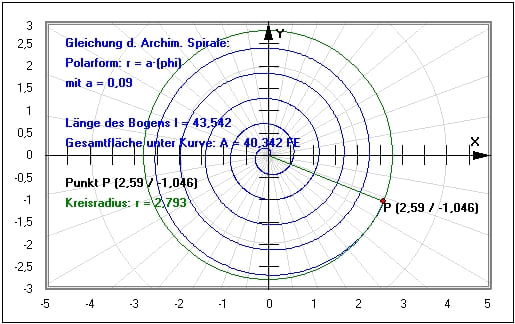
Als Kurve c nehmen wir eine beliebige Gerade c(t) = P+t·V. Ein beliebiger Kreis oder eine beliebige Kugel mit Mittelpunkt Z und Radius r hat die Gleichung ( X − Z )2 = r 2 .Damit haben wir für nach Bogenlänge parametrisierte Kurven eine Formel, mit deren Hilfe wir die Krümmung einfach berechnen können.ZujederregulärenparametrisiertenKurveγ: I→R3 .Krümmung berechnen.Es gibt verschiedene Verallgemeinerungen der ursprünglich von Archimedes beschrieben Spirale, für die in der Literatur auch oft archimedische Spiralen als Sammelbegriff verwendet wird.

Hierbei wird die ursprüngliche Gleichung r=a\cdot \varphi r = a ⋅φ zu r=a\cdot \varphi^\frac {1} {d} r = a ⋅φd1 mit d\in\mathbb {R} d ∈ R erweitert. parametrisiert.Die Klothoide, auch Klotoide (von griechisch κλώθω ‚spinnen‘), ist eine spezielle ebene Kurve. Die Bogenlänge einer Kurve und der Krümmungsradius einer Kurve werden durch recht hässliche Formeln bestimmt.Schlagwörter:KurveKrümmung
Krümmung von Kurven
Dazu wird in Gl. Zeigen Sie, dass F .Ergänzung: http://weitz. (t) = r (cos (ωt), sin (ωt)) mit ω = 1/r.Es handelt sich um eine Bogenlängen-Parametrisierung, . Wir suchen diejenigen Kreise oder Kugeln, die die Kurve in A (mindestens) dreifach berühren.Schlagwörter:KurveKrümmungAuthor:Edmund WeitzPublish Year:2019
Kurven
Die Windung beschreibt zusammen mit der Krümmung das lokale Verhalten der Kurve und kommt wie die Krümmung als Koeffizient in den Frenet’schen Formeln vor. Die Gaußsche Krümmung, benannt nach Carl Friedrich Gauß, ist gleich dem Produkt der Hauptkrümmungen, k 1 k 2.(Analogfür c : I →R 2 ) 1 KURVENTHEORIE 5
Bogenlänge einer Kurve
Die Krümmung ist also durch den Betrag der Ableitung des Einheitstangentenvektors $ {\vec {t}}={\frac {\mathrm {d} {\vec {r}}}{\mathrm {d} s}} $ nach . Andere Bezeichnungen für die Klothoide sind Cornu-Spirale (nach Marie . Die Windung beschreibt zusammen mit der Krümmung das lokale Verhalten der Kurve und kommt wie die Krümmung als Koeffizient in den frenetschen Formeln vor. Es gibt sogar eine allgemeinere Formel, . Dabei gibt es drei Möglichkeiten, wie sie aussehen kann: f“(x) ist eine negative Zahl (z.
Krümmungsradius und Bogenlänge einer Kurve bestimmen
Klothoide
letzte Krümmung heißt auch Torsion der Kurve. z Die Kurve kann somit nicht nach Bogenl ̈ange parametrisiert werden. Vorlesung 05 (22. Mit einem anschaulichen Beispiel erklären wir dir die Definition der Krümmung und Torsion im Raum.
Das Buch der Ellipsen
A ∈ SO (2) und b ∈ R².deEmpfohlen basierend auf dem, was zu diesem Thema beliebt ist • FeedbackQuaternionen, reguläre Kurven, Parametertransformation, Umparametrisierung, nach Bogenlänge parametrisierte Kurven, die Länge einer Kurve (Definitionen durch Integral und Supremum). Krümmung und Krümmungskreise.
Parametrisierung nach der Bogenlänge
Dabei gibt es drei . Ein zentrischer Kreis K r mit Radius r wird durch f : [ 0, 2r π ] → ℝ2 mit.
- Krieg Der Sterne Fsk , Krieg der Sterne
- Kuba Regierungspräsidenten _ Liste der Ministerpräsidenten und Ministerratspräsidenten Kubas
- Криминальное Чтиво Смотреть Онлайн Бесплатно
- Kuchen Mit Quarkfüllung , Omas Rührkuchen mit Quark: Schnell & Saftig in 10 Minuten
- Küchen Prozente Aktion – Rösle Grill im Angebot: Gasgrills und Holzkohle-Kugelgrills im Sale
- Ktm Alskom Motoräder , KTM YAMAHA QUAD Goldspeed Räder vorne neu
- Ks Tools Katalog Online , Sockets
- Krups Perfect Mix 9000 Pro Manual
- Ktm 125 Lc2 , Ktm Lc 2 125, Motorrad gebraucht kaufen
- Kroschke Erste Hilfe – Rettungszeichen & Fluchtweg Piktogramme kaufen
- Küchenradio Mit Lautsprecherbelastung