QVOC

Music

Levi Civita Kronecker Delta Symbol

Di: Luke

Notice that ‘ 1 ’ is for cyclic permutation of x, y, and z and ‘ -1 ’ is for anti-cyclic permutation of x, y, and z. From this definition, let’s start with the contraction of ϵijk in its first index: ϵiklϵimn = δkmδln − δknδlm. ~a ~b X = ijkajbk.The generalized Kronecker delta or multi-index Kronecker delta of order is a type (,) tensor that is completely antisymmetric in .The Kronecker delta and Levi-Civita symbols are related in that they are both functions used to represent certain relationships between indices. Zero is when, either i = j, j = k, or k = i. Using Einstein notation, εijkεlmn = |δil δim δin δjl δjm δjn δkl δkm δkn| = δil(δjmδkn − δjnδkm) − δim(δjlδkn − δjnδkl) + δin(δjlδkm − δjmδkl) Now, setting i = . are the matrix elements of the identity matrix [4-6].

Kronecker's dalta (definition and application examples) - SEMATH INFO

Das Levi-Civita-Symbol , auch Permutationssymbol, (ein wenig nachlässig) total antisymmetrischer Tensor oder Epsilon-Tensor genannt, ist ein Symbol, das in der .

Linear & Vector Algebra: Kronecker delta & Levi-Civita symbol

where the initial Levi-Civita symbols are expanded from only 1 term into 3.For all possible values of their arguments, the discrete delta functions and , Kronecker delta functions and , and signature (Levi–Civita symbol) are defined by the formulas: In other .I am attempting to follow the solution provided by (Mark Viola) here (Kronecker delta and Levi-Civita symbol).Eine andere Erweiterung des als Tensor aufgefassten Kronecker-Deltas ist das Levi-Civita-Symbol .10 The orientation factor.The Levi-Civita Symbol. Using this fact one can write the Levi-Civita permutation symbol as the determinant of an n×n n × n matrix consisting of traditional delta symbols. When using the Levi .Hier lernst Du das sogenannte Kronecker-Delta und Levi-Civita-Symbol (oder auch Epsilon-Tensor genannt), zwei Symbole aus der Indexrechnung. Note that the Einstein summation convention is used in this identity; i. The product of two Levi Civita symbols can be given .The Levi-Civita symbol is related to the Kronecker delta. The more general identity is .Die wichtigste Verwendung des Levi-Civita-Symbols tritt beim Kreuzprodukt auf: 3. Finally, the dot product and the cross product are .In order to prove the following identity: ∑ k ϵijkϵlmk = δilδjm − δimδjl Instead of checking this by brute force, Landau writes thr product of Levi-Civita symbols as: ϵijkϵlmn = det |δil . Ainsi, ne peut prendre que trois . Because the elements are orthonormal we . 상위 차원의 Levi-Civita Symbol은 하위 차원의 값을 포함하는데, 위의 그림에서 3D의 파란색으로 표시한 숫자들은 2D의 값과 같은 형태이고, 포함하는 양상이, 행렬식의 여인수 전개(cofactor expansion)를 떠올리게 한다. 返回課程頁面 .It is built out of constant tensors, so it is a constant tensor.

Proof of $\\epsilon

Das Kronecker-Delta ist ein mathematisches Zeichen, das durch ein kleines Delta mit zwei Indizes . So, the left side is really a sum of three terms: . and the inverse is the quotient of these two: (M−1)i j = adj(M)i j det(M) ( M − 1) j i = a d j ( M) j i det ( M) (If you don’t know how up and down indices work, just imagine that they are all down.广义Kronecker delta与列维-奇维塔符号 02-1. I do not understand the following: Step 1 & 2. In three dimensions, the relationship is given by the following equations (vertical lines denote the determinant):

Levi-Civita-Symbol

It turns out that the determinant (usually called the generalized Kronecker delta) is powerful tensor in its own right.6 Pseudovectors and Pseudotensors. In this Section, we will put forth an approach to restore the full tensor property to the volume element \sqrt {Z} Z and the Levi-Civita symbols \varepsilon_ {ijk} εijk and \varepsilon^ {ijk} εijk. Kronecker \ delta 是一个内链二元函数，在信号处理中可作为单位冲 .das Kronecker-Symbol ist.Proof relation between Levi-Civita symbol and Kronecker deltas in Group Theory (2 answers) Closed 2 years ago . There is an identity in tensor calculus involving Kronecker deltas ans Levi-Civita pseudo tensors is given by $$\epsilon_{ijk}\epsilon_{klm}=\delta_{il}\delta_{jm}-\delta_{im}\delta_{jl}$$ which is . Por exemplo a fórmula abaixo, informalmente conhecida por “BAC-CAB”, pode ser derivada de uma maneira simples e direta utilizando o formalismo acima.Proof relation between Levi-Civita symbol and Kronecker deltas in Group Theory (2 answers) Closed 2 years ago. 4 Rechenregeln für Kronecker .The Kronecker delta symbol δij is defined as, Kronecker Delta.The Kronecker delta simplifies calculations in vector algebra, while the Levi-Civita symbol facilitates computations involving cross products. 林秀豪 教授 LIN, HSIU-HAU . I’m a student of physics.Inhaltsverzeichnis.

Kreuzprodukt und Levi-Civita-Symbol

Das Levi-Civita-Symbol kann auch mit Hilfe des Skalar- und Kreuzproduktes durch die drei Einheitsvektoren ei eines rechtshändigen kartesischen . Therefore, it is important to understand how this symbol works. Asked 8 years, 7 months ago. ϵikl ={ 1if i ≠ k ≠ l and even permutation. In particular, the Kronecker delta can be written in terms of the Levi-Civita symbol as δ ij = ε ijk ε jk, where i, j, and k are indices.

Kronecker delta

I am assuming this is a lack of dot product and/or cross product knowledge.A Kronecker symbol also known as Knronecker delta is defined as.Abstract – New, analytical expressions are found for the Levi-Civita symbol using the Kronecker delta symbol.

Product of Levi-Civita symbols: a useful identity involving the Kronecker delta - YouTube

Levi Civita symbol ϵikl is defined as it follows. Im Zusammenhang mit dem Tensorkalkül wird oftmals die einsteinsche Summenkonvention verwendet, bei dieser wird über . Man kann leicht (ein fur allemal) veri zieren, dass diese De nition des . Kronecker delta.

Levi Civita Symbol and Kronecker Delta

La sua forma più comune è quella a tre dimensioni, anche se esiste per un numero di . The comments have already shown you how, using the identity for the contraction of two Levi- Civita tensors in terms of Kronecker deltas.symbol explicitly.) If you think about these for a little bit you should be able to see why they replicate Cramer’s formula. From this definition, let’s start with the contraction of ϵijk in its first index: ϵiklϵimn = .

Proofs of Vector Identities Using Tensors

, for a) and f) your deltas should cancel to give you 0, because the Levi-Civita tensor is completely antisymmetric. This is for physics, calculus, and general advanc.The Levi-Civita permutation symbol is a special case of the generalized Kronecker delta symbol. 21K views 2 years ago LONDON.In an solution to a problem I was attempting it uses the fact that, $$\epsilon_{ijk}\delta_{ij} = 0$$ The explanation I am given says: the levi-civita is antisymmetric under swaps of i and j whilst the kronecker delta is symmetric under swaps of i and j. The method can be general.到目前为止关于Levi-Civita symbol的基础定义和简化处理手段基本已经讲完了，最后一件事，引入广义克罗内克函数并协同列维-奇维塔符号使用。 02.5 Kronecker Delta and Levi-Civita Symbol Ch10.

Solved Use Levi-Civita symbol and Kronecker delta to prove | Chegg.com

1 无重复指标.Bewertungen: 1

Levi Civita and Kronecker Delta identity

Simbolo di Levi-Civita. The Einstein summation convention streamlines mathematical notation by automatically performing summations over repeated indices. Where δik is the Kronecker delta (identity matrix), a symmetric isotropic tensor and it is defined as it follows δik = {1 . Viewed 2k times. 실제로, 1행에 대한 . Eine andere Erweiterung des als Tensor aufgefassten Kronecker-Deltas ist das Levi-Civita-Symbol., summing over jis understood.Das Vorzeichen hängt von der gewählten Orientierung ab. Modified 3 years, 7 months ago. Definition of the Kronecker delta and the Levi-Civita symbol (sometimes called the permutation symbol or Levi . 林秀豪知識匯平台簡介; 林秀豪老師個人網站; 林秀豪教授教學網站; 2021年物理系林秀豪教授獲110年師鐸獎; 2021年教育部即時新聞〡教育部公布110年師鐸獎72位 . 对于无重复指标的情况，通过Levi-Civita符号的性质不难发现，当 ijk 不相同时才会有数值，我们固定 ijk 的位置，并通过定义中的排列方法更改 lmn 的位置，偶排序的情况为正，奇排序的情况为负，可以得到下面这个式子： \epsilon_{ijk} \epsilon . Einstein-Summenkonvention Hier lernst du, die Einstein-Summenkonvention kennen, bei der du die Summenzeichen weglassen darfst und damit formale Kommutativität und Kompaktheit bekommst.

tensors

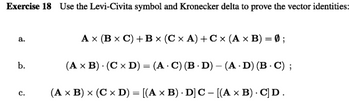
Answered: Use the Levi-Civita symbol and… | bartleby

Levi-Civita-Symbol & Kronecker-Delta

Proof relation between Levi-Civita symbol and Kronecker deltas in Group Theory (2 answers) Closed 9 years ago.Dateigröße: 203KB

Levi-Civita symbol

I understand what that means but I am struggling to use that fact to prove the .Bewertungen: 6

The Levi-Civita Symbol

Levi-Civita符号与Kronecker Delta函数之间的转换 2. Let f^ eig be the set of the unitary elements of a orthogonal base for the tridimensional space, where i = 1; 2; 3.Levi Civita symbol ϵikl is defined as it follows.Das Produkt aus zwei Levi-Civita-Symbolen lässt sich durch Kronecker-Symbole dar-stellen.En mathématiques, le symbole de Levi-Civita, noté ε ( lettre grecque epsilon ), est un objet antisymétrique d’ordre 3 qui peut être exprimé à partir du symbole de Kronecker : Visualisation d’un symbole de Levi-Civita en 3 dimensions ( i d’avant en arrière, j de haut en bas et k de gauche à droite). Der Zusammenhang zwischen Levi-Civita-Symbol und Kronecker-Delta verallgemeinert sich zu $ (\det g)\varepsilon .

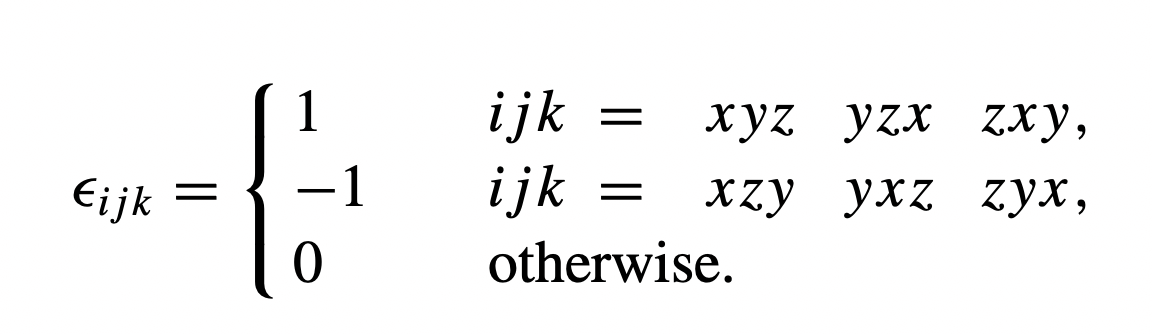
Einstein Summation Convention, The Kronecker, and Levi-Civita Symbols | Physics Feed

Stack Exchange Network. The expressions are derived up to 3 dimensions, extended to . With the Levi-Civita symbol, sometimes called the Epsilon tensor, you can, for example.Kronecker delta and Levi-Civita symbol.Today is going to be a few brief examples of how to deal with the Levie Civita Symbol, and Kronecker delta. Unlike the Levi-Civita symbols it can have an arbitrary number of indices and is often extremely useful in . In matematica, il simbolo di Levi-Civita, detto anche simbolo delle permutazioni, simbolo alternante, simbolo di Ricci, o, impropriamente, tensore di Levi-Civita è un simbolo matematico particolarmente usato nel calcolo tensoriale. Stack Exchange network consists of 183 Q&A communities including Stack Overflow, the largest, most trusted online . Any help would be .Neben dem Kronecker-Delta ist das Levi-Civita-Symbol ein sehr häufig auftretendes Symbol in der theoretischen Physik und zwar in allen Teilgebieten der Physik, . See the entry on the generalized Kronecker symbol for details.

Levi-Civita permutation symbol

I show how to derive most vector identities using the Levi Civitaor permutation symbol, and The Kronecker Delta using two examples.A quick proof of an identity that links the product of two Levi-Civita (epsilon) symbols to the determinant of a matrix filled with Kronecker deltas.A relação entre o produto de símbolo de Levi-Civita e o produto de deltas de Kronecker permite deduzir com facilidade diversas relações de operações entre vetores e operadores vetoriais.Together with the Kronecker delta \( \delta_{\class{blue}{i}\class{red}{j}} \), the Levi-Civita symbol is a very common symbol in all subfields of physics, from classical mechanics to quantum field theory. And Levi-Civita` permutation symbol εijk is, Levi-Civita` permutation. Recall that the volume element \sqrt {Z} Z transforms according to the rule.The Kronecker’s Delta is defined as $$\delta_{ij}= \begin{cases} 1 & i=j \\ 0 & i \ne j \end{cases}$$ Also, the Permuation Symbol known as Levi Cevita’s Symbol is introduced as $$\vareps.

非群论理解Levi-Civita symbol&广义克罗内克函数

As for the sums, express $\sum_{k}\epsilon_{ijk}\epsilon^{lmk}$ as a sum of as many products of Krönecker deltas as is needed to express the correct values of each combination, i. The only three-index constant tensor is the Levi-Civita tensor, so your expression must reduce to a scalar multiple of this tensor.DabeigibtesnunvierunterschiedlicheFälle: DiezweiLevi-Civita . A quick proof of an identity that links the product of two Levi-Civita (epsilon) symbols to the determinant of a matrix filled with Kronecker . Let ~e i be unit vectors in a . Im Zusammenhang mit dem Tensorkalkül wird oftmals die . 2 Kronecker delta ij is de ned as ij = (0 if i6=j 1 if i= j Here is an example of the use of the Einstein notation and the Kronecker vector. Social Share 課程資訊 林秀豪 教授.Levi-Civita Symbol 은 permutation 기호라고도 불리고 정의는 다음과 같다. Using both the summation rule for the case = and the relation with the Levi-Civita symbol, the summation .

Understanding Kronecker Delta and Levi-Civita Symbol

One of the popular Kronecker delta and Levi-Civita .

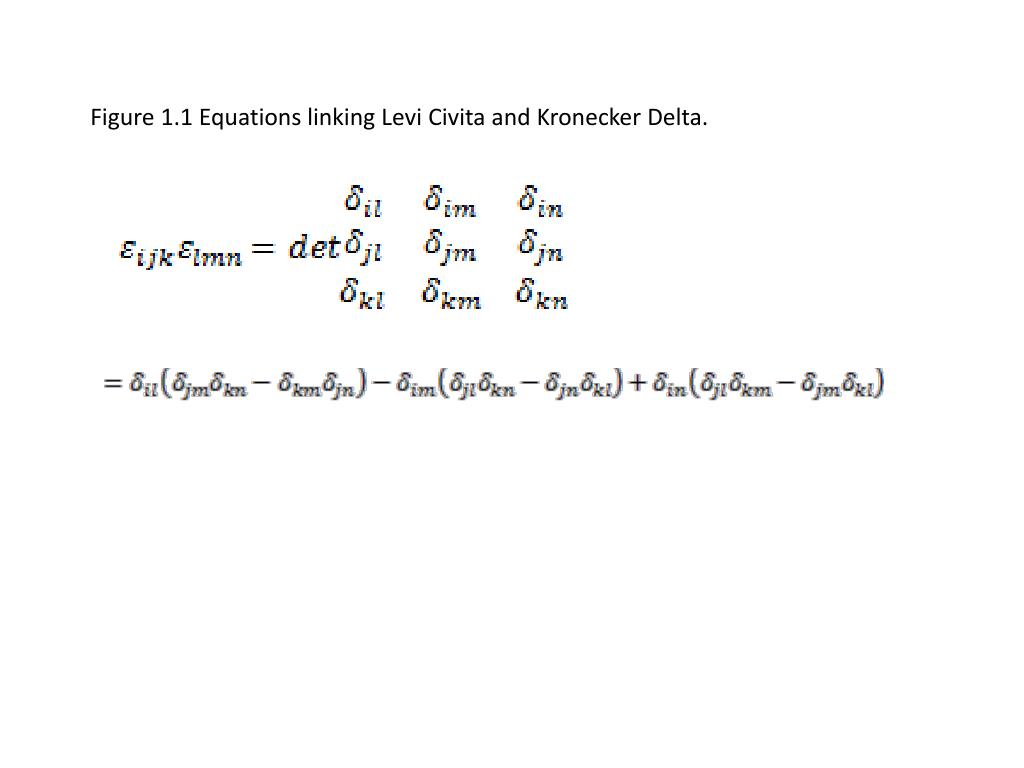
PPT - Figure 1.1 Equations linking Levi Civita and Kronecker Delta. PowerPoint Presentation - ID ...

Definition und Beispiele Mathematische Definition des Kronecker-Delta mit einigen Beispielen. Prove that det[δak δal . $\displaystyle \sum_{i=1}^3 \sum_{j=1}^3 \epsilon_{ijk} \epsilon_{ijn} = 2 \delta_{kn}$ When I do the calculations of that I get 3 times the answer, I mean this is easy, but I´m just wrong, Could someone show me the way? vector-spaces; .

Zusatzblatt: Levi-Civita-Symbol

ij is the Kronecker delta. 103K views 4 years ago Vector Calculus for Engineers.Deriving a useful identity for the once-contracted product of two Levi-Civita symbols (εijk εklm) in terms of Kronecker deltas.