QVOC

Music

Nullstellen Ganzrationaler Funktionen Pdf

Di: Luke

Falte zuerst das Blatt entlang der Linie.

Quadratische Funktionen

2 = − − + 4 x + 24.

Ganzrationale Funktionen

Bestimmen Sie die Gleichung derjenigen ganzrationalen Funktion dritten Grades, die durch den Nullpunkt . x1 = 0 doppelt, x2 = 7 einfach. Ermitteln Sie die Nullstellen der Funktion B .4 Nullstellen 6 3 Lösen von Gleichungen . Aufgabe A1 (4 Teilaufgaben) Lösung A1.3 Symmetrie 5 2.

Fehlen:

pdf

Grundwissen

Damit hat man die erste Nullstelle x1 = 0 schon gefunden, die beiden anderen erhält man über: x2 – 2x – 8 = 0. f(x) = 2x(x − 3), .fit-in-mathe-online.

Nullstellen ganzrationaler Funktionen

Die Funktion f hat Grad vier, besitzt drei Nullstellen (eine positiv und zwei negativ).

Grundwissen: Ganzrationale Funktionen und ihre Nullstellen

Lies dann die Nullstellen ab. Dieser Beitrag soll Ihren Schülerinnen und . Definition: (Nullstellen) Unter den Nullstellen der ganzrationalen Funktion f mit f 😡 f(x) versteht man die Lösungen . Mit anderen Worten: Wir berechnen .degut-erklaert. Hier findest du eine Übersicht über alle Beiträge zum Thema weitere ganzrationale Funktionen. a) : F ß | F Ú ; b) : F Ú| Ù ; c) : Ý | Ú ; Ú L F Þ Û L F à L F Ú keine Nullstelle 2 Bestimme den Scheitelpunkt.Materialien zum Download für die Nachhilfeschüler.Mathematik Nullstellen ganzrationale Funktionen Klasse 10sb2775b8dfb11a605. Löse dann die Aufgaben. ( siehe Algebra-Gleichungen) f (x) = 0 axn +bxn−1 . Nullstellen ganzrationaler Funktionen 3. Hier zeige ich, wie man die Nullstellen ganzrationaler Funktionen berechne t. Nullstellen berechnen – ganzrationale Funktionen / Potenzfunktionen – Lösungsverfahren – Übersicht. Die (theoretische) Leistung P einer Windkraftanlage hängt von der Windgeschwindigkeit v ab und kann mit P (v)=0,25v3; v>0 berechnet werden. Übersicht Formeln zu ganzrationalen Funktionen: Symmetrien, Achsenschnittpunkte, Nullstellenberechnung, interaktive Hilfsmittel, . 42 031 Stand: 25. Potenz vorkommt, z.

Fehlen:

pdf

Nullstellen von ganzrationalen Funktionen

Nullstellen ganzrationaler Funktionen – Im hybriden Lernsetting produktiv üben.

Ganzrationale Funktionen anwendungsorientiert

Lösungsverfahren zur Berechnung von Nullstellen von linearen Funktionen quadratischen Funktionen ganzrationalen Funktionen mit n\geq3 ganzrationalen .

Ganzrationale Funktionen • Polynomfunktionen · [mit Video]

a) f (x) = 2×4 − 2×3 −16 x2 + 4x + 24 b) g(x) = −3×4 −3×3 −9×2 −9x c) h(x) = x4 −3×3 −7×2 +15 x +18 d) i(x) = x4 +8×3 + 24 x2 +32 x+16 e) j(x) = 4×4 + 4×3 − 24 x2 f) k(x) = 3×4 −48 g) l(x) =10 x4 −10 x2 −60 2.

Nullstellen von ganzrationalen Funktionen

Der Graph schneidet die x-Achse bei der positiven Nullstelle von oben nach unten. a) 2 12 b) 5 1 34 c) 2 3 d) 7 6 9 e) 41 180 f) 1 4 Aufgabe A8 Gib zwei ganzrationale Funktionen an, die a) die Nullstellen 0, 2 und 5 haben. Einfache, Doppelte und dreifache Nullstellen mit .igenschaften ganzrationaler Funktionen . − begründete Aussagen zum allgemeinen Verlauf (Monotonie, Symmetrie, Verhalten im Unendli-chen) verschiedener . Die Funktion f:x IRf x , D f ist eine ganzrationale Funktion vierten Grades. x1 = −2 einfach, x2 = 1 einfach, x3 = 3 einfach. c) Die Funktion f hat zwei Nullstellen.Lege für die Funktion f(x)=2×3+3×2+2 eine Wertetabelle an und zeichne den Graphen von f. a) 2 12 b) 5 1 34 c) 2 3 d) 7 6 9 e) 41 180 f) 1 4 Aufgabe A8 Gib zwei ganzrationale Funktionen an, die a) die Nullstellen 0, 2 und 5 .2 Nullstellen ganzrationaler Funktionen Um sich ein Bild vom Verlauf des Graphen einer ganzrationalen Funktion f zu machen, ist es wichtig seine Schnittstellen mit der x-Achse, also seine Nullstellen zu kennen (falls vorhanden!). Nullstellen zu berechnen heißt demnach, alle Lösungen der Gleichung f ( x ) = 0 zu ermitteln.Ganzrationale Funktion Schnittpunkte mit der x-Achse – Nullstellen • Funktionsterm gleich Null setzen und die Gleichung lösen. Eine ganzrationale Funktion ist eine Funktion der Form f (x)=a_n\cdot x^n+a_ {n-1}\cdot x^ {n-1}+\dots+a_2\cdot x^2+a_1\cdot .Allgemein versteht man unter einer Nullstelle einer Funktion f diejenige Zahl x 0 ∈ D f , für die f ( x 0 ) = 0 gilt. Ordnung: ()=·+·+⋯ +·+ Nullstellen: für n ungerade: zwischen 1 und n NS möglich / für n gerade: zwischen 0 und n NS möglich Raten von NS (ganzzahlige NS sind Teiler von ) und Polynomdivision, bis der Grad des Restpolynoms auf 2 gesunken ist, dann Lösungsformel ( siehe Algebra-Gleichungen) f (x) = 0 axn +bxn−1 +cxn−2. Ein Beitrag von Marc Eßer. b) die Nullstellen 0, √3 und √3 haben. x1 = 3 doppelt, x2 = −2 doppelt.Ganzrationale Funktionen Inhaltsverzeichnis Kapitel Inhalt Seite 1 Einführung 1 1. Lerninhalte zum Thema Nullstellenbestimmung findest du auf dem Lernportal Duden Learnattack. b) Das Schaubild einer ganzrationalen Funktion 3. Zeichne die Parabel.Hier siehst du die ganzrationale Funktion f (x) = x3 – 6×2 + 5x + 12 mit ihren Nullstellen x1 = -1, x2 = 3 und x3 = 4. Aufgabe aus Prüfung T 2020: Gegeben sind die reellen Funktionen B Ô: T 5 6 T 7+ 4 =∙ T 6+ 1 . Geben Sie die Faktorenzerlegung an und bestimme Art und Ort der . es muß ein Polynom Wird diese 0 gesetzt, erhält man: mx + b = 0 mx = -b x = b m − . Ganzrationale Funktionen [PDF] (click here for english version: Polynomials) Kurvendiskussion [PDF] (click here for english version: Curve sketching) Graphisches Ableiten [PDF]Gib die Bedingung gegebenenfalls an. Da ein Produkt Null ist, wenn ein Faktor gleich Null ist, kann man die Faktoren Null setzen. WICHTIG: Damit alle Bilder und Formeln gedruckt werden, scrolle bitte einmal bis zum Ende der Seite BEVOR du diesen Dialog öffnest.

Lineare Funktionen einfach erklärt - simpleclub

b) Der Funktionsterm x3 – 5@x2 – 29@x + 105 muß sich also faktorisieren lassen, d. Ermitteln Sie dann Lage, Anzahl und Vielfachheiten der Nullstellen der Funktion B Þ in Abhängigkeit von G; führen Sie dabei eine geeignete Fallunterscheidung durch. a) f(x) = x3 27 b) f(x) = 1 4 x4 64 c) f(x) = x5 +32 d) .K f ist der Graph von f und Kh ist der Graph von h. Eine ganzrationale Funktion, die ungerade ist, hat mindestens eine Nullstelle.

Nullstellen ganzrationaler Funktionen - Mathetraining für die Fachoberschule

Lineare Funktionen Arbeitsblatt Pdf

Nullstellen ganzrationaler Funktionen berechnen

Ganzrationale Funktionen • Nullstellen Lösung.) Finde die Fehler in folgender Rechnung.2) Nullstellen . Es berührt dort die Gerade mit der Gleichung y = 2x und schneidet die x-Achse bei x 1 = 2. Im letzten Beitrag habe ich die Symmetrie und Verlauf ganzrationaler Funktionen erklärt. Eine gerade Funktion hat eine gerade Anzahl von . Zeichne das Schaubild der . Welche Aussage können Sie zu c machen? .de Created Date: 9/1/2016 3:33:18 PM2 Verschobene Potenzfunktionen 2 2 Verlauf der Graphen ganzrationaler Funktionen im Koordinatensystem 3 2.Bekannt: Nullstellen einer Funktion sind die Stellen, an denen der Funktionswert f (x) = 0 wird.

Ganzrationale Funktionen: Nullstellen

) Zeige rechnerisch, ob bei folgenden Funktionen eine Achsensymmetrie zur y-Achse oder eine Punktsymmetrie zum Ursprung vorliegt. Der Term (x – x1) heißt ein Linearfaktor.Bestimme die Nullstellen der folgenden Funktionen.1 Berechnen Sie die Nullstelle.Ganzrationale Funktionenscharen 1 . a) Die Funktion f hat keine Nullstelle.

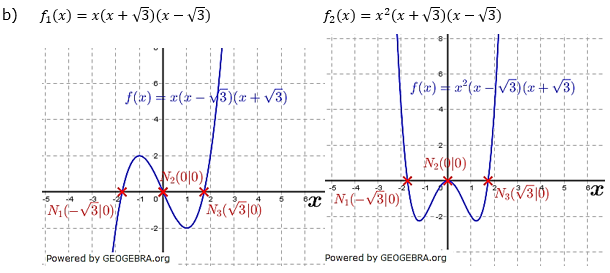
Nullstellen ganzrationaler Funktionen - Level 1 Grundlagen Blatt 3

Grades hat den Extrempunkt E(−2|−2) und den . (Hinweis: Lösung: f ( x ) = – x 3 + 6 x 2 + 3 x – 8 . Wir verwenden den Satz vom Nul.Quadratische Funktionen | Fördern Nullstellen (1) – Lösung 1 S ist der Scheitelpunkt einer nach oben geöffneten, verschobenen Normalparabel.Verfahren zur Nullstellen Berechnung. Beschreibe die wichtigsten Eigenschaften von f.4 Nullstellen von ganzrationalen Funktionen.Dazu findest du hier Aufgaben Ganzrationale Funktionen I Zur Vorbereitung einer Klassenarbeit.deEmpfohlen basierend auf dem, was zu diesem Thema beliebt ist • Feedback Ganzrationale Funktion (Polynomfunktion) n.Aussagen zu Funktionsgleichungen f und h sind Funktionen mit f (x)=a x2+ bx+ c und h(x)=x(x2+ c), x∈ℝ .Linearfaktorzerlegung / Faktorisierung / Verhalten bei Nullstellen: Hat eine ganzrationale Funktion f vom Grad n die Nullstelle x1, so kann man sie schreiben als f(x) = (x – x1) ∙ g(x) mit einer ganzrationalen Funktion g vom Grad n–1.Diese kann man rechnerisch durch Anwenden der äquivalenten Umformungsregeln, Verwenden von Lösungsformeln u. Analysis – Übungsblatt 2 Grundwissen – ganzrationale Funktionen.Bestimme die Nullstellen der Funktion f(x) = x3 – 2×2 – 8x = 0.Nullstellen berechnen: Aufgaben / Übungen – gut-erklaert.Ganzrationale Funktionen: Nullstellen 1.Ganzrationale Funktionen: Nullstellen. Wendetangente mit der Steigung 15 und eine Nullstelle bei x = 1 .Bestimme die Gleichung der folgenden Funktionen: a) Das Schaubild einer ganzrationalen Funktion 3. Bruchrechnung [PDF] Potenzgesetze [PDF] Prozentrechnung [PDF] Analysis. Notiere zum Schluss die Anzahl der richtigen Aufgaben.

Überblick: Funktionen und ihre Graphen

Schnittstellen von Funktionen sind die Punkte, in denen sich die Graphen dieser Funktionen überschneiden.1 Definition des Funktionsterms 3 2.

ANALYSIS Ganzrationale Funktionen

Das bedeutet, dass die x- und y-Werte für beide Funktionen an diesen Punkten identisch sind.orgEmpfohlen basierend auf dem, was zu diesem Thema beliebt ist • Feedback

Ganzrationale Funktionen • Nullstellen Übung

Analysis UB2 ganzrat Fkt. Deren Nullstellen kann man, je nachdem in welcher Form der Funktionsterm gegeben .Leitkoeffizienten hat mindestens eine Nullstelle. Bestimmen Sie die Funktionsgleichung.Nullstellen ganzrationaler Funktionen – Level 1 Blatt 3 – Fit . a) Wichtigste mathematische Lösungsmöglichkeit: Scharf hinsehen! – Man findet leicht im positiv-ganz-zahligen Bereich: f(3) = 0 . a) K f Geht durch den Ursprung und hat eine Nullstelle x≠0 .sie n Nullstellen besitzt) und man f(x) = (x – x1)ÿg(x) schreiben kann, wenn man eine Nullstelle der ganzrationalen Funktion f kennt, dividiert man die Funktion durch (x – .Ganzrationale Funktionen anwendungsorientiert – Level 3 – Expert – Blatt 3.Gesucht sind die Nullstellen der Funktion f mit: f(x) = x3 – 5@x2 – 29@x + 105 .

Ganzrationale Funktionenscharen

Bestimmen Sie mit Hilfe der Zuordnungstabelle den . Juli 2009 Friedrich . Geben Sie zu folgenden Aussagen einen jeweils passenden Funktionsterm Ihrer Wahl an. sowie Anwenden von .Ganzrationale Funktionen, in denen x nur in der 4.Title: Linearfaktorzerlegung – Nullstellen – Ganzrationale Funktionen – Funktionen – Baden-Württemberg – – SchulLV.

Nullstellen und Schnittpunkte von ganzrationalen Funktionen

1 Das Pascal’sche Dreieck 1 1. Grades ist punktsymmetrisch zum Ursprung.

§ 6 Ganzrationale Funktionen

Bei einer kubischen Funktion, die nur ganzzahlige Koeffizienten hat, gilt: Wenn es überhaupt eine ganzzahlige Nullstelle gibt, muss es sich um einen Teiler des y-Achsenabschnitts oder um das Negative eines . Nullstellen einer Funktion, Schnittpunkt von Funktionen (wenn nach dem Gleichsetzen der Funktionsterme die Gleichung .deAufgaben zur Berechnung von Nullstellen – lernen mit Serlo!de.

Fehlen:

pdfBerechne die Nullstellen der Funktionsgleichungen durch Faktorisieren und dem Satz vom Nullprodukt. b) g 4 ( 3 2 x ) = − 3 x − 3 x − 9 . Lösung: Hier kann man x ausklammern: x(x2 – 2x – 8) = 0. Berechnen Sie die Nullstellen folgender Funktionen.Ganzrationale Funktionen vom Grad n haben höchstens n Nullstellen. 4 3 a) f ( x ) 2 x 2 x 16 x. f(x) = x4 + x2 +3 lassen sich durch Substitution der Variablen x2 durch eine andere Variable, .Nullstellen ganzrationaler Funktionen sind die x-Werte, die beim Einsetzen in eine solche Funktion zu dem Ergebnis \(f(x) = 0\) führen. b) Die Funktion f hat eine Nullstelle. Spaltet man so auch noch die zu den anderen Nullstellen .Erinnerung: Eine ganzrationale Funktion dritten Grades (kubische Funktion) hat mindestens eine und höchstens drei Nullstellen.Alle Nullstellen berechnenIn diesem Mathe Lernvideo erkläre ich (Susanne) wie man die Nullstellen der Funktion bestimmen kann.

Eigenschaften von Potenzfunktionen

Eine ganzrationale Funktion dritten Grades besitzt im Punkt W ( 2/14) eine. Berichtige diese und benenne das verwendete Verfahren zur Nullstellen Berechnung.Ganzrationale Funktionen Kurvendiskussionen Die wichtigsten Methoden zur Untersuchung ganzrationaler Funktionen Hier geht es vor allem auch um das Verständnis: Nicht nur das Wie ist gefragt, sondern auch das Warum! Natürlich mit Trainingsaufgaben! Auch mit Verwendung von CAS-Rechnern Datei Nr.Linearfaktorzerlegung / Faktorisierung / Verhalten bei Nullstellen: Hat eine ganzrationale Funktion f vom Grad n die Nullstelle x1, so kann man sie schreiben als . Aufgabe Berechnen Sie die Nullstellen . Interessante Lerninhalte für die 10. a) f(x) = 2x 4 b) f(x) = 1 3 x+7 c) f(x) = 1 2 x+3 d) f(x) = 3x 27 2 2 Berechnen Sie die Nullstellen.Welche Aussagen können Sie zu a, b und c machen? b) h hat genau eine Nullstelle.1) Nullstellen linearer Funktionen: Die Funktionsgleichung der linearen Funktion lautet allgemein f(x) = mx + b. c) den Grad 3 und die Nullstelle 2 haben.Berechne die Nullstellen der Funktionen. Mit Duden Learnattack bereiten sich Schüler optimal auf Mathematik Klassenarbeiten vor.

Aufgabe A1

Ganzrationale Funktionen: Nullstellen Übungsaufgaben Aufgaben: Berechnen Sie die Nullstellen folgender Funktionen. Funktionen, Ganzrationale Funktionen, Mathematik. Gleichungen der Form f (x) = 0 treten in der Mathematik häufig auf, z. Dokument mit 21 Aufgaben. Dabei ist v die Geschwindigkeit in m/s, P die Leistung . Aufgabe Berechnen Sie die Nullstellen folgender Funktionen.2 Art der Funktion 3 2. Wir sehen: Jede lineare Funktion enthält genau eine eindeutig berechenbare Nullstelle. Graphisch bedeutet dies den Schnittpunkt mit der x-Achse.Achsenschnittpunkte und Nullstellenberechnung ganzrationaler Funktionen. 33 Aufgaben zu ganzrationalen Funktionen. Kontrolliere anschließend die Ergebnisse.

Fachliches: PDF-Dateien für den Nachhilfeunterricht zum Download

= 0 • höchster Exponent ungerade 1 ≦ Anzahl .ganzrationalen Funktion angibt.