QVOC

Music

Nullvektorraum Beispiel – Orthogonale Projektion · Herleitung & Beispiel · [mit Video]

Di: Luke

Lösung : Von Vektoren ist in dieser Aufgabe keine Rede, aber wir benutzen sie als Werkzeug, um schnell ans Ziel zu kommen: Mit A und M kennen wir auch den Verbindungsvektor

Orthogonale Projektion · Herleitung & Beispiel · [mit Video]

Nehmen wir als Beispiel den Vektorraum der Ebene. Der Koordinatenraum ist hier , bei reellen oder komplexen Vektorräumen also bzw. Der Nullvektorraum ist bis auf Isomorphie der .

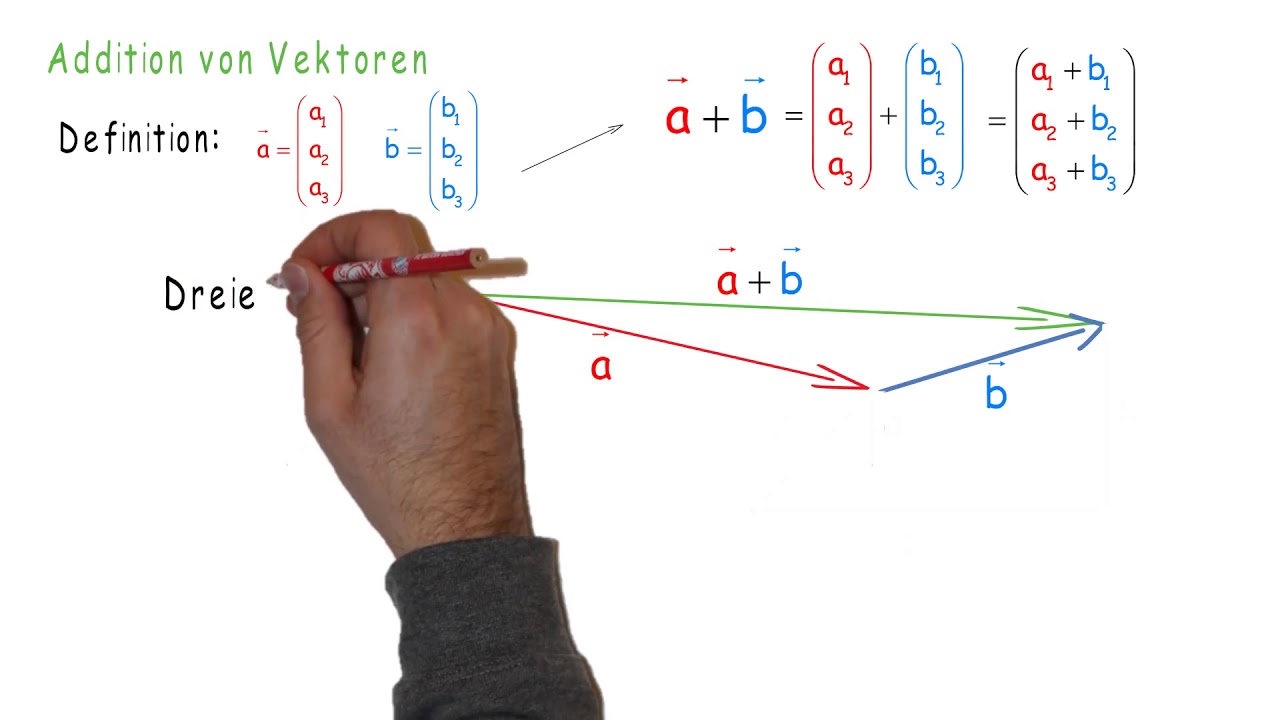
Rechnen mit Vektoren (inkl. Gegenvektor und Nullvektor)_Erklärvideo - YouTube

Die Menge aller Vektoren der reellen Zahlenebene bildet mit der üblichen komponentenweisen Vektoraddition und Skalarmultiplikation einen Vektorraum.1o {0} und V sind Untervektorr ä ume von V.Beim Nullraum (auch Kern) einer Matrix handelt es sich um die Menge aller Vektoren, die durch die Multiplikation mit der Matrix auf den Nullvektor abgebildet werden. In der Mathematik sagt man statt senkrecht auch häufig, dass der Vektor orthogonal zu etwas ist. der Multiplikation stehen.1 Einige Beispiele. Als Pfeil der Länge Null . Danach sollten erst die Grundrechenarten wie Addition und Subtraktion mit Vektoren gelernt werden.Der Nullvektorraum ist der Vektorraum, in dem nur der Nullvektor als Element enthalten ist. Noch ein Hinweis: Ich erhalte öfters einmal E-Mails mit verschiedenen Vorschlägen für die Achsenbeschriftungen, in denen verschiedenste x, y und z Achsen vorgeschlagen werden.Vektor & Gegenvektor bestimmen + Beispiel mit Lösung. Zwei Koffizienten sind ungleich null, zwei gleich null.Versuche einmal, im Applet, das du unten ausklappen kannst und das du schon von der Kursseite Beispiel:Aufstellen des Vektors zwischen zwei Punkten kennst, einen . 0 → = ( 0 | 0) = ( 0 0) A A → = 0. Wir definieren eine Addition und eine Skalarmultiplikation durch. Aber in gibt es . Dies sind die Funktionen der Form

Vektoren 1

Die Formel zum Berechnen des Betrags für einen Vektor →v = (v1 v2) im zweidimensionalen Raum lautet: |→v | = √v2 1 + v2 2. Der Nullvektorraum (auch Nullraum) ist in der Mathematik ein Vektorraum, der nur aus einem Vektor, dem Nullvektor, besteht. Ihr könnt es euch so Vorstellen, dass v Vektoren sind und die Elemente aus K einfach die . Beispiel 1: Es ist zu prüfen, ob die beiden Vektoren. Wir betrachten den $\mathcal V = \mathbb{R}^2 .Nullvektorraum. Der Vektorraum 0, genannt der Nullvektorraum, der nur aus einem Ele . Weitere Beispiele von Vektorr ä umen: (10. Auch da erkennt man, dass der Normalenvektor n → senkrecht auf der Ebene E: x → steht. (03:04) In diesem Beitrag erklären wir den Begriff Vektorraum und wie du beweisen kannst, dass eine Menge einen Vektorraum definiert.Um eine Basis zu bilden, müssen die Vektoren zueinander linear unabhängig sein.Wir haben schon oben bei der Herleitung drei Beispiele für Teilmengen des gesehen, die keinen Untervektorraum bilden. Schaft und Spitze vom Nullvektor fallen in einem Punkt zusammen. (02:35) In diesem Artikel erklären wir dir anhand verschiedener Beispiele, was eine Linearkombination ist und wie du sie berechnest. Das kann eine Gerade, eine Ebene, eine Fläche oder auch eine gekrümmte Linie, wie zum Beispiel ein Kreis, sein.

Nullvektor

Vektor in der Ebene und Raum

In einem Skalarproduktraum ist der Nullvektor orthogonal zu allen Vektoren des Raums.Beispiele für Vektorräume.Der Nullvektorraum (auch Nullraum) ist in der Mathematik ein Vektorraum, der nur aus einem Vektor, dem Nullvektor, besteht.Es gibt zwei Schreibweisen für Ortsvektoren, die dir vielleicht über den Weg laufen. Klick hier für eine Übersicht der unterschiedlichen Lernfunktionen und erfahre in 3 Minuten, wie du mit serlo.Dies ist im obigen Beispiel der Fall.org richtig nutzen. Daraus ergibt sich folgende Gleichung: 3 • 2 + 1 • 6 + 4 • b 3 = 0 Wichtig: Du kannst beliebige Variablen wählen, außer den Vektor ! Damit ist zwar das Skalarprodukt gleich null, aber der Vektor besitzt keine Länge. Allgemeine Definition. Gv := f v j 2 Rg; wobei v 2 2. Allgemein handelt es sich beim Kern einer linearen Abbildung zwischen Vektorräumen um die Menge aller Vektoren, die auf den Nullvektor abgebildet werden. Zum besseren Verständnis betrachten wir nun auch für . Dabei dürfen wir nicht den Nullvektor verwenden. ( { 0 }, +, ⋅) Der Nullvektorraum ist der kleinste Vektorraum, den es gibt (nur ein . Schau dir gerne auch noch unsere Videos zu einer Übungsaufgabe und einer beispielhaften Klausuraufgabe .Beim Nullvektorraum (auch Nullraum ) handelt es sich um einen Vektorraum, der lediglich ein einziges Element, den Nullvektor, enthält. Beispiel 1: Länge ebener Vektor. mit v 6= 0, und der Vektorraum 2. (00:12) Linearkombination berechnen. 27K views 8 years ago. Damit wird zu einem -Vektorraum, genannt . Raum der affinen Funktionen [Bearbeiten] Ein anderer Vektorraum ist der Raum der affinen Funktionen auf den reellen Zahlen.Unter Verwendung des Begriffes Linearkombination lässt sich nun äquivalent formulieren: Die Vektoren heißen linear unabhängig, wenn sich kein Vektor von ihnen als Linearkombination aus den übrigen darstellen lässt. Der Verbindungsvektor beginnt dann bei A (Fußpunkt) und endet bei B (Spitze) .In unserem Beispiel setzen wir b 1 = 2 und b 2 = 6 ein. Beispiel: Der Vektor zwischen zwei Punkten A (2|1) und B (6|4) ist.Beispiele für Nullvektoren sind die Zahl Null, die Nullmatrix und die Nullfunktion. Die Teilmenge der Vektoren, für die gilt, bildet einen Untervektorraum von , denn es gilt für alle : . Dank dieser Werbung bleibt StudySmarter . Ein Normalenvektor (oder Normalvektor) ist ein Vektor, der senkrecht auf etwas anderem steht. Mathematik in 5 Minuten by Alexander Stöger. Längen und Winkel kamen ja gar nicht vor, und das Koordinatensystem konnte ebensogut schiefwinklig sein.Autor: Mathematik in 5 Minuten by Alexander StögerIn der Mathematik spielt das Konzept des Vektorraums eine zentrale Rolle.Was ist der Nullvektor? – Mathematik in 5 Minuten.

Matrizenraum

Vektorraum, Erzeugendensystem, lineare Hülle, Basis

Beispiel 3: d-dimensionaler Euklidischer Raum: (z. Der Nullvektor hat keine Länge und damit auch keine Richtung. Im dreidimensionalen Raum sieht das für den Vektor →v = (v1 v2 v3) so aus: |→v | = √v2 1 + v2 2 + v2 3. Er kann nicht als Pfeil dargestellt werden. Raum von Ortsvektoren) In einem Euklidischen Raum gibt es keinen ‚ausgezeichneten‘, ‚besonderen‘ Punkt. Download chapter PDF. Der Nullvektorraum ist in jedem Vektorraum als Untervektorraum enthalten.Vektor berechnen einfach erklärt.Der Nullvektor ist das neutrale Element bezüglich der Addition von Vektoren.Normalenvektor einfach erklärt.Die Untervektorraume von R2 sind der Nullvektorraum f0g.Diese wird dann zum Beispiel in ein x-y-z-Koordinatensystem eingetragen. Mit Hilfe von Vektoren können also Richtungen repräsentiert werden. Länge ebener Vektor Formel.Euklidische VektorräumeLineare Abhängigkeit

Nullvektorraum

Linearkombination einfach erklärt. Hier siehst Du eine Abbildung des Normalenvektors n → = 0 – 1 3 im Koordinatensystem. Am Anfang ist es wichtig, die Vektoren erst mal zu verstehen und bestimmen zu können. Nun ist ein Pfeil nichts anderes als ein Vektor. Man kann sich ein Vektorfeld räumlich so vorstellen, als würde in jedem Punkt vom Zimmer in dem man sitzt, ein Vektor seinen Anfangspunkt haben. Dies ist wohldefiniert, denn ist und.

Nullvektorraum

Online-LernCenter

Dimension eines Vektorraums

Im Folgenden wollen wir uns mit Vektoren und Gegenvektoren beschäftigen. Jeder Vektorraum enthält den Nullvektorraum als kleinstmöglichen Untervektorraum. In der Praxis sieht es so aus, dass man die Achsen entsprechend der Aufgabenstellung . Die Anzahl der maximal möglichen linear unabhängigen Vektoren gibt die Dimension des Vektorraumes an. Dieser Artikel führt dich detailliert in die Materie ein, erklärt Begriffe, liefert Beispiele und hilft dabei, praxisnahe Aufgaben zum .Lineare Abhängigkeit: prüfen Definition Vektoren Matrix Beweis Unabhängigkeit Beispiel StudySmarter Original

Linear unabhängige Vektoren (Linearkombination)

Der Normalenvektor der Ebene E: x → ist n → = 0 – 1 3. Springe zu: Vektor bestimmen. Die Standardbasis für den Matrizenraum besteht aus den Standardmatrizen, bei denen .

Vektorräume in der linearen Algebra

Ein Beispiel hierfür ist . Eine Richtung können wir mit einem Pfeil darstellen: Pfeil, der eine Richtung in der Ebene markiert. Dass dies nicht geschehen kann, wird nun im nächsten Satz bewiesen:

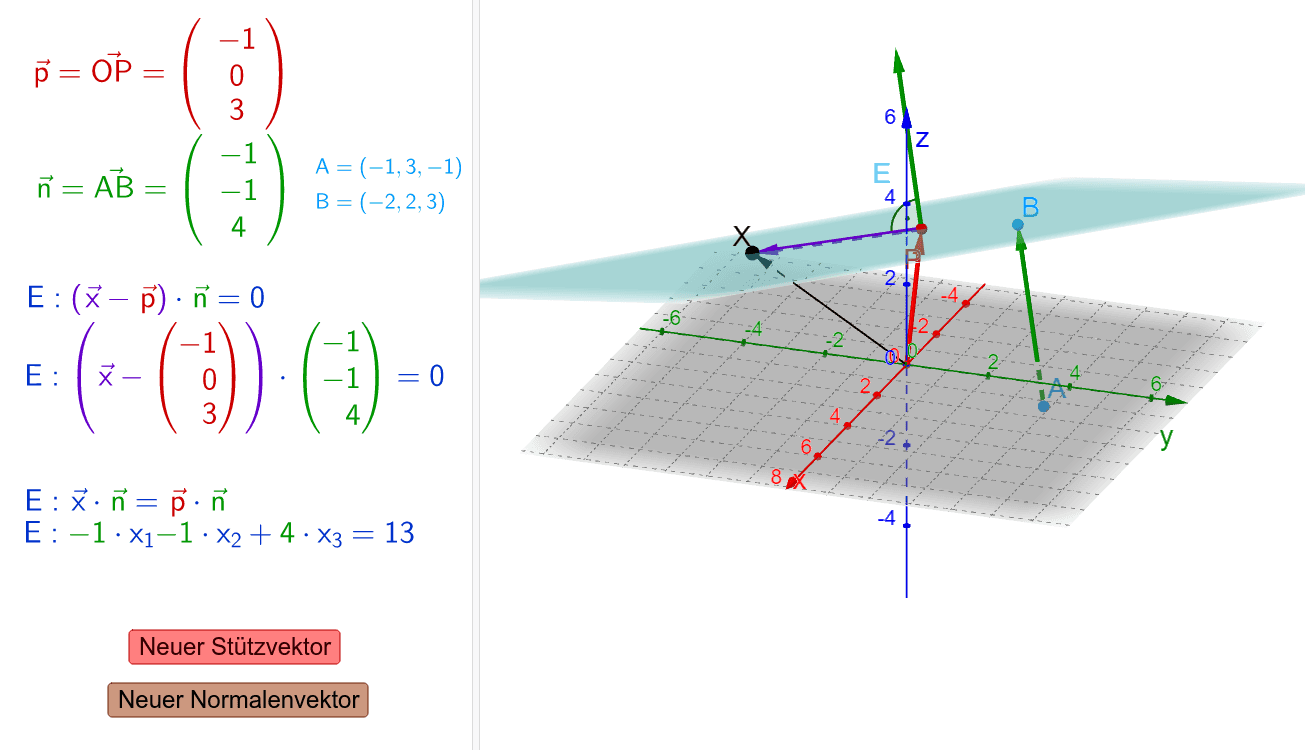
Ebenengleichung in Normalen- und Koordinatenform – GeoGebra

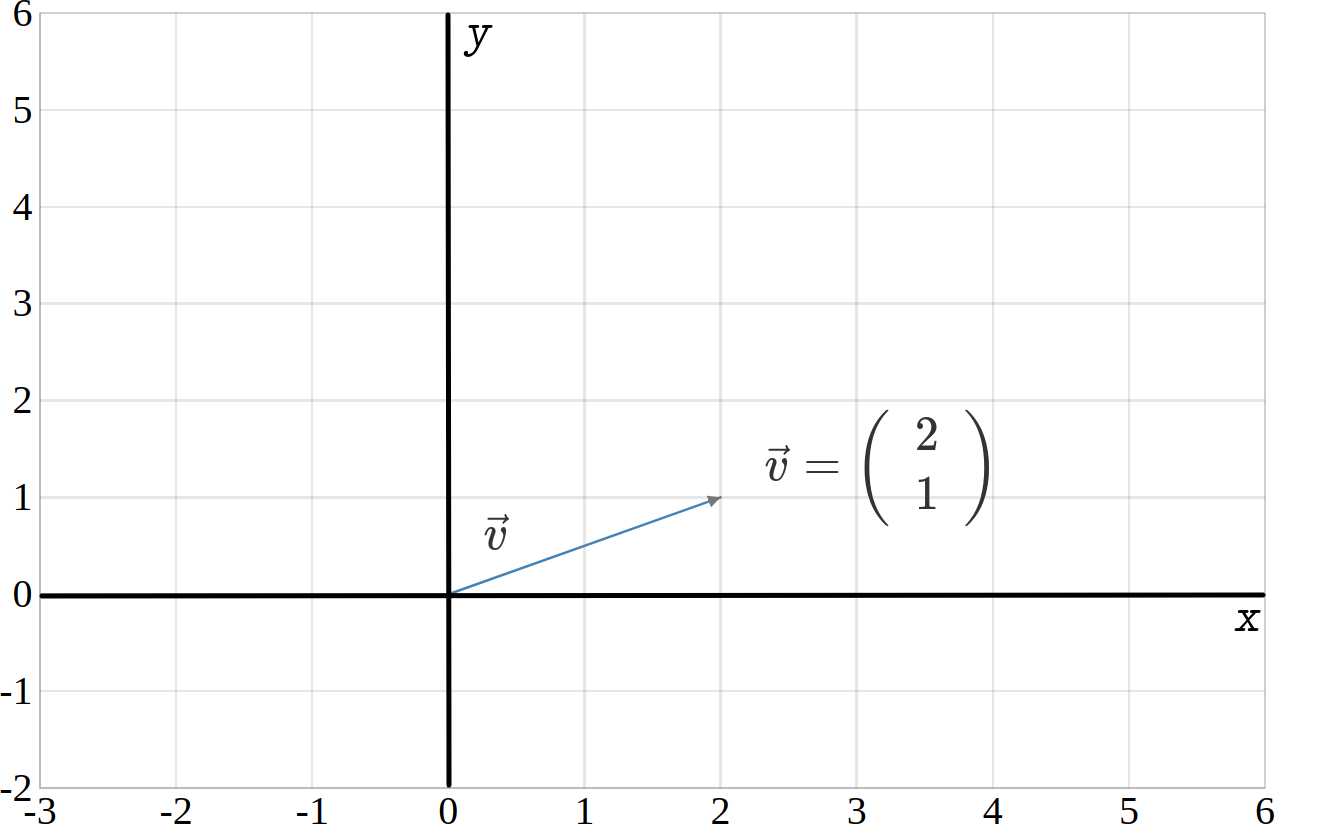
Vektorrechnung leicht erklärt Vektorrechner - Simplexy

Der Matrizenraum oder Raum der Matrizen ist in der Mathematik der Vektorraum der Matrizen fester Größe über einem gegebenen Körper mit der Matrizenaddition und der Skalarmultiplikation als innerer und äußerer Verknüpfung.Konkrete Beispiele. Abbildung 3: Normalenvektor n der Ebene E:x im Koordinatensystem. Die Dimension der euklidischen Ebene ist 2, die des Raumes 3.In diesem Artikel zeigen wir dir, was eine orthogonale Projektion ist und welche Rolle das Skalarprodukt dabei spielt. Eine Menge von Vektoren ist linear abhängig, wenn man eine Linearkombination von ihnen bilden kann, die den Nullvektor ergibt und nicht trivial ist (trivial wäre, einfach von allen .Man sagt modulo .Beispiele für Vektorfelder sind der Wärmefluss oder die elektrische oder magnetische Feldstärke. Wir müssen ihn jedoch definieren, da wir ihn zum Beispiel bei .

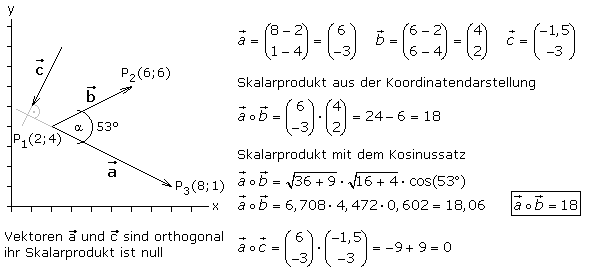
Vektoralgebra

Beispiele für Nullvektoren.

Bild Einer Matrix - 04A.1 Rang, Spaltenraum, Defekt, Kern einer Matrix ...

Insbesondere folgt daraus bereits, dass drei Vektoren im R 2 \mathbb{R}^2 R 2 immer linear abhängig sind, da sie sich alle in einer Ebene befinden.Übersicht

Vektorraum • einfache Erklärung + Beispiele · [mit Video]

Mit $\lambda_{1,2} = 0$, $\lambda_3 = 4$ und $\lambda_4 = \frac{1}{3}$ kann der Vektor $\vec{v} = (8,1)$ abgebildet werden.Aus dieser Definition wird nicht klar, dass die Dimension unabhängig von der Wahl der Basis unseres Vektorraums ist. Es könnte zum Beispiel passieren, dass ein Vektorraum verschiedenen Basen mit unterschiedlich vielen Elementen besitzt.Im Beispiel ist der Koordinatenvektor von der Form („Nummerierung“ der Koordinaten).Alles zu diesem Beispiel Gesagte gilt schon in der reellen affinen Ebene. 3o {(r,s,0) : r,s aus K} ist ein Untervektorraum .

Vektorrechnung in der Ebene und im Raum

Viel Spaß damitSuper Formelsammlung zum Nachschlagen http://am. zur Stelle im Video springen. Ein zweidimensionaler Nullvektor: a = (0 0) a = ( 0 0) Ein dreidimensionaler Nullvektor: b = ⎛⎝⎜0 0 0⎞⎠⎟ b = ( 0 0 0) Dadurch schließen die Vektoren und keinen rechten Winkel ein.

Untervektorraum

Beispiel: Von einem Parallelogramm sind die Punkte A(0, 1) und B(4, 2) sowie der Mittelpunkt M(3, 4) gegeben. Wenn wir der Intuition folgen wollen, dass dreidimensional ist, müssen wir noch einen dritten Vektor finden, der zu dem System linear unabhängig ist. Besonders in Bereichen wie lineare Algebra und Analytik ist das Verständnis für Vektorräume, ihre Eigenschaften, Basis und Dimension essentiell.

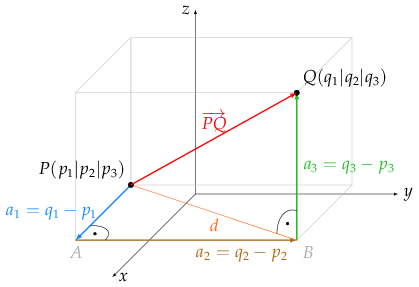
Vektor Berechnen Formel

Der Raum \ (\mathbb {R}^ {\boldsymbol . Wir betrachten dazu im Folgenden zwei Beispiele. Der Nullvektorraum ist bis auf Isomorphie der einzige Vektorraum mit Dimension und seine Basis ist die leere Menge. Eine Basis ist ein Erzeugendensystem mit linear unabhängigen Vektoren.

Ortsvektor - Definition erklärt inkl. Übungen

Als Beispiele werden hauptsächlich reelle Vektorräume herangezogen. Er ist, von Isomorphie abgesehen, der .Dazu haben wir einen Vektor (erkennt man an dem Pfeil über dem v) mit x und y.Video ansehen1:34Hallo Leute, heute was ist der Nullvektor? Es ist das neutrale Element der Vektorrechnung. Die Länge dieses Vektors berechnet man in dem man die Wurzel aus x 2 + y 2 zieht. Verbindungsvektor zwischen zwei .

Lineare Unabhängigkeit von Vektoren

Du musst also die einzelnen Komponenten eines Vektors jeweils quadrieren, dann miteinander .

Vektorraum ausführlich erklärt

der Koordinatenursprung liegt in ; Als weiteres Beispiel kann man den . Offenbar ist der K¨orper Kselbst mit seiner Addition und Multiplikation ein Vektorraum. Er ist, von Isomorphie abgesehen, der einzige Vektorraum der Dimension 0; seine Basis ist die leere Menge. Bei der ersten schreibst du einfach ein großes „O“, dann den jeweiligen Punkt, wo der Ortsvektor hinführt und dann noch einen Pfeil nach rechts darüber: (Ortsvektor zu Punkt A) Alternativ werden Ortsvektoren manchmal auch als Kleinbuchstaben mit einem Pfeil darüber . Gesucht sind die (Koordinaten der) Punkte C und D .5) Beispiele: Sei V eine Vektorraum ü ber K. Jeder dieser unendlich vielen Vektoren würde in jene Richtung zeigen, in der sich die Temperatur im .

Beispiele für Vektorräume

Der Betrag des Vektors erkennt man an der Schreibweise mit zwei Betragsstrichen. (00:13) Um den Vektor zu berechnen, der die Punkte A und B verbindet, musst du A von B abziehen. Wenn du die orthogonale Projektion in unter 5 Minuten verstehen willst, dann schau dir gerne unser Theorievideo dazu an.org hat viele Features, die dir beim Lernen helfen.

Betrag und Normierung

Habe ich im Dreidimensionalen drei zueinander linear unabhängige Vektoren gefunden, so gibt es . Die Untervektorraume von . Hier soll 1 K das neutrale Element in K bzgl.org erfolgreich lernen kannst! R2, die Geraden. {0} mit 0 + 0 = 0 0+ 0 = 0 und 0 =\alpha 0 0 = α0 für alle \alpha\in K α ∈ K ist ein K-Vektorraum, der Nullvektorraum.35K subscribers.