QVOC

Orthogonale Basis : Orthogonal bases and projections

Di: Luke

Frage zur Anwendung vom Orthogonalen Komplement und allgemein zur Diagonalisierbarkeit.Orthogonalprojektion eines Punkts auf eine Ebene : Der Verbindungsvektor zwischen dem Punkt und seinem Abbild ′ bildet mit der Ebene einen rechten Winkel.Bestimme eine orthogonalbasis, sodass nur die Werte 1,-1,0 auf der Diagonalen auftreten.Zusammenfassung: In diesem Abschnitt wir der Begriff der Orthogonalität und einer orthonormierten Basis erläutert. Umkehrung: Einen orthogonalen Vektor finden Wenn man nachweisen kann, dass ein Vektor zu einem anderen Vektor orthogonal ist, dann kann man diesen Nachweis logischerweise auch umkehren und auf diese Weise herausfinden, welcher Vektor zu einem anderen Vektor orthogonal liegt. Die Basis ist ein Rechtssystem, wenn die Vek-toren ~u, .Eine Orthonormalbasis (ONB) oder ein vollständiges Orthonormalsystem (VONS) ist in den mathematischen Gebieten lineare Algebra und Funktionalanalysis eine Menge von .Orthogonale Basen.

Bestimmen Sie eine orthogonale Basis des R3, die aus

Orthogonalität und orthonormierte Basen

Let’s check that this works by considering the vector b = [ 1 0 0] and finding , b, its orthogonal projection onto the plane . Start practicing—and saving your progress—now: https://www. Basis ( vi) i∈I eines euklidischen oder unitären Vektorraumes ( V, ·, · ) aus paarweise orthogonalen Vektoren vi, d. ich hoffe du hast eine Idee wie das funktionieren könnte. Wie das Verfahren.We frequently ask to write a given vector as a linear combination of given basis vectors. eine unitäre Abbildung (im komplexen Fall) und ist eine Orthonormalbasis von , so ist die Darstellungsmatrix von bezüglich der Basis eine orthogonale bzw.Eine Orthogonalbasis eines euklidischen Vektorraumes (V,h,,i) ist eine Basis von V, die eine orthogonale Menge ist.Mit dem Gram Schmidt Orthogonalisierungsverfahren lässt sich eine orthogonale Basis bestimmen, die den selben Vektorraum aufspannt, wie die ursprünglichen Vektoren.b) Bestimmen Sie das charakteristische Polynom von A A und geben Sie die Eigenwerte von A A an. Zeigen kann man dies, indem das Skalarprodukt aller Basisvektoren v i * v j, mit i != j immer Null ergibt.Eine orthogonale Abbildung oder orthogonale Transformation ist in der Mathematik eine Abbildung zwischen zwei reellen Skalarprodukträumen, die das Skalarprodukt erhält. Beweis einer orthogonalen Matrix: Berechne die Transponierte der gegebenen Matrix, multipliziere sie mit der ursprünglichen Matrix und überprüfe, ob das Ergebnis die Einheitsmatrix ist. Man muss natürlich das Senkrechtstehen der Vektoren nicht durch Probieren zusammenbasteln, da gibt’s schon auch Algorithmen dafür – den Gram-Schmidt-Algorithmus nämlich. Basis B = [b1,. ὀρθός orthós gerade, γωνία gōnía Winkel und lat. d) Bestimmen Sie eine orthogonale Matrix S \in \operatorname {Mat} (3,3) S ∈ Mat(3,3), so dass S^ {\top} A S S⊤AS eine .

Orthogonale Matrix: Beweis & Determinante

c) Berechnen Sie die Koordinaten von w in .v 2 = (4,2,5) T und v 3 = (-1,2,0) T. wenn du eine Orthonormalbasis hast, brauchst du nur die.

Orthogonale Basen

Die Basis ist ein Rechtssystem, wenn die Vek-toren ~u, ~v, w~ gem aˇ der Rechten-Hand-Regel orientiert sind (Daumen !~u, Zeige nger!~v, Mittel nger !~w), bzw. Zwei Vektoren . normiert sind).An orthogonal basis of vectors is a set of vectors {x_j} that satisfy x_jx_k=C_(jk)delta_(jk) and x^mux_nu=C_nu^mudelta_nu^mu, where C_(jk), C_nu^mu are constants (not necessarily equal to 1), delta_(jk) is the Kronecker delta, and Einstein summation has been used. The preview activity illustrates how this task can be simplified when the basis vectors are orthogonal to one another.Die Orthogonalbasis ist diejenige deren Vektoren alle im rechten Winkel aufeinander stehen.The Gram-Schmidt orthogonalization is also known as the Gram-Schmidt process. huj; uki = 0; j 6= k : Eine normierte orthogonale Basis, d. ~u; ~v; ~w ; jeweils ungleich ~ 0., B⋅BT ist eine Diagonalmatrix. b) Konstruieren Sie eine orthonormale Basis {b1, b2, b3} des ℝ 3 mit b1 ∈ ℝu1 und b2 ∈ ℝu2.Aufgabe 1075: Eigenwerte und orthogonale Basis aus Eigenvektoren für eine 4×4-Matrix. die Aufgabe die ich lösen möchte ist folgende: Es sei V:= ℝ 4 mit dem Standardskalarprodukt versehen und es sei U der von den Vektoren.

Bestimmen einer Basis des orthogonalen Untervektorraums

Ein Vektor besitzt bzgl. Eine Orthogonalbasis ist eine Basis in der jedes Paar von Vektoren senkrecht zueinander steht. Eigenschaften einer orthogonalen . (hier alles über n anstatt n) Def. Gefragt 24 Apr 2020 von Mark.Das Gram-Schmidt-Verfahren wandelt eine beliebige Basis eines euklidischen Vektorraums in eine orthogonale Basis um. Gefragt 26 Jan 2023 von firestorm.

Eine Basis B = fu1; : : : ; ung eines Vektorraums V ist orthogonal, wenn. Folgende Grafik verdeutlicht den Zusammenhang: Senkrechte Projektion eines Vektors b auf den .Courses on Khan Academy are always 100% free.Eine Orthonormalbasis eines Innenproduktraums ist in der linearen Algebra und der Funktionalanalysis eine Basis dieses Vektorraums, deren Vektoren alle die Länge (die Norm) 1 haben (also Einheitsvektoren sind), und die .

Orthogonal Basis

Eine orthogonale Basis im Raum besteht aus drei paarweise orthogonalen Vektoren. ist , so spricht man von einem Orthonormalsystem oder einer Orthonormalbasis. In the past, we have done this by solving a linear system.In der Funktionalanalysis versteht man unter einer Orthonormalbasis ein maximales Orthonormalsystem in einem Hilbertraum; ein Synonym hierzu ist vollständiges .

Gram-Schmidt-Verfahren

15 tells us that.

TU Dresden, WS 2013/14 Einfuhr¨ ung in die Mathematik fur¨ Informatiker Folie 4. As we will see later, orthonormal bases have many special properties that allow us to simplify various calculations. Im euklidischen Raum können orthogonale Abbildungen durch orthogonale Matrizen .a) Zeigen Sie, dass u1, u2 und u3 keine orthogonale Basis des ℝ 3 bilden.Contributors; We now define the notions of orthogonal basis and orthonormal basis for an inner product space.Eine Menge von orthogonalen Vektoren, die alle vom Nullvektor verschieden sind, ist immer linear unabhängig und bildet deshalb eine Basis der linearen Hülle dieser Menge. ich habe eine Frage zu folgender Aufgabe: Sei W⊆ℝ 4 der Unterraum, der von u= (1,0,-1,2) und v= (2,0,2,-1) aufgespannt . Satz: Jede Basis B besitzt eine äquivalente orthogonale Basis B* , bestimme B* durch Gram-Schmidt-Orthogonalisierung (GSO) bi* : = bi . Bestimme eine Basis des zu U ortogonalen Untervektorraums. Aufgabe 1219: Eigenschaften von Orthogonalsystemen. Eine Orthogonalprojektion (von gr. Stichworte: Defintion | Orthonormierte Basis | Theoreme. Bezüglich beliebiger Basen ist diese Aussage falsch. Ein Vektor besitzt . Da v‘ eine Linear­kombination von u und v ist, erzeugen die orthogonalen Basis­vektoren denselben Unterraum U. einer orthogonalen Basis die Darstellung Für die Koeffizienten gilt . Ist eine orthogonale (im reellen Fall) bzw. b ^ = b ⋅ w 1 w 1 ⋅ w 1 w 1 + b ⋅ w 2 w 2 ⋅ w 2 w 2 = [ 29 / 45 4 / 9 8 / 45] ?.Orthogonale Abbildungen. und wie kann ich diese überprüfen.Orthogonale Basis.Das dient in diesem Artikel als Basisfall, auf dem später aufgebaut werden soll.

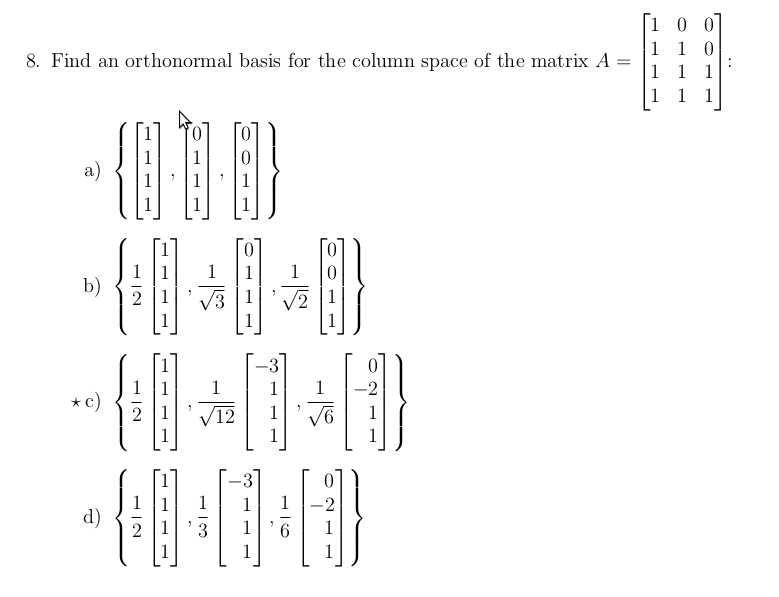
Hierzu muss man nur herausfinden, welcher gesuchte . Ein euklidischer Vektorraum . Spalten jeweils mit einem geeigneten Faktor zu multiplizieren, dass 1 oder -1 in der Diagonale rauskommt.Übersicht

Orthogonal basis

Bestimmen einer Basis des orthogonalen Untervektorraums.Orthogonale Basis in der Ebene und im Raum Eine orthogonale Basis im Raum besteht aus drei paarweise orthogonalen Vektoren ~u; ~v; w~ ; jeweils ungleich ~0. Nun ist {v 1 ,v 2 ,v 3 } eine Orthogonalbasis aus Eigenvektoren.Standardskalarprodukt Basis des orthogonalen Komplements.Für unitäre/orthogonale Abbildungen gilt: falls Unitäre/orthogonale Abbildungen finden in der Physik vielfältige Anwendungen: – Theorie der Rotationen in klassischer Mechanik & .

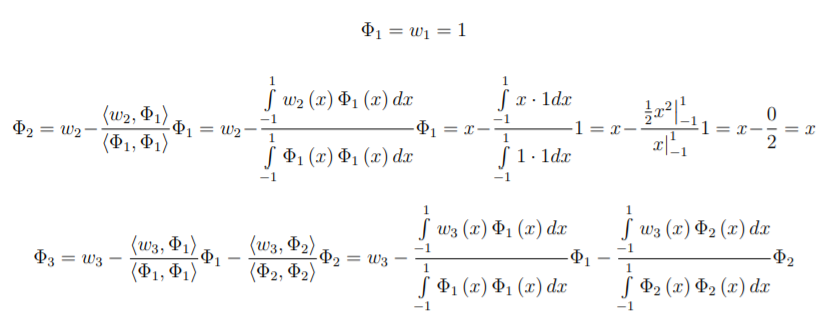
Eine Orthonormalbasis ist eine Orthogonalbasis in der die Basisvektoren die Länge 1 haben (d. The orthogonal basis calculator is a simple way to find the orthonormal vectors of free, independent vectors in three dimensional space.

Online-Gram-Schmidt-Prozessrechner, orthogonale Vektoren mit Schritten finden aquivalent da-

Gram Schmidt Calculator

Let \(V \) be an inner product space with inner product \(\inner{\cdot}{\cdot}\). Die Orthogonalbasis ist diejenige deren Vektoren alle im rechten Winkel aufeinander stehen. prōicere, PPP prōiectum vorwärtswerfen), orthogonale Projektion oder senkrechte Projektion ist .Basis (vi)i∈I eines euklidischen oder unitären Vektorraumes (V, 〈·, ·〉) aus paarweise orthogonalen Vektoren vi, d. 0,2],[-5,-9,-8,6]}.2: Orthogonal and Orthonormal Bases Last updated; Save as PDF Page ID 2086; David Cherney, Tom Denton, & Andrew Waldron; University of California, Davis .

Orthogonal bases and projections

Unterschied von Orthonormalbasis und Orthogonalbasis

Zeigen kann man dies, indem das Skalarprodukt aller Basisvektoren . 1) U=Span{[1,-1,-1,-1],[1,0,1,-2],[1,0,0 . was ist eine Orthonormalbasis.Wenn du die orthogonale Projektion in unter 5 Minuten verstehen willst, dann schau dir gerne unser Theorievideo dazu an. Orthogonale Abbildungen sind stets linear, injektiv, normerhaltend und abstandserhaltend. In terms of the original basis w 1 and , w 2, the projection formula from Proposition 6.

Gram-Schmidt-Rechner

Eine Orthonormalbasis von V ist eine Basis von V, die eine orthonormale Menge ist. Du kannst also auch erstmal eine Basis aus . If the constants are all equal to 1, then the set of vectors is . Schau dir gerne auch noch unsere Videos zu einer Übungsaufgabe und einer beispielhaften .orthonormal basis of (1, 2, -1),(2, 4, -2),(-2, -2, 2) Natural Language; Math Input; Extended Keyboard Examples Upload Random.

Orthonormalbasis

Overview

Orthonormalbasis: Definition, Anwendung

Auf dieser Konstruktion beruht das Gram-Schmidt . Interaktive Aufgaben: Interaktive .Orthogonalbasis.2: Orthogonal and Orthonormal Bases Expand/collapse global location 14. (2,1,0,3) , (4,2,1,-1) und (1,0,2,-13) erzeugte Untervektorraum von V.Interaktive Aufgabe 120: Orientierung einer Basis, Koeffizientenbestimmung bezüglich einer Orthonormalbasis. Darstellung in Koordinaten einer Orthogonalbasis Theorem 33: Es . jukj = 1 8 k, wird als . standardskalarprodukt; orthonormalbasis; komplement + 0 Daumen.org/math/linear-algebra/alternate-bases/. In which we take the non-orthogonal set of vectors and construct the orthogonal basis of vectors and find their orthonormal vectors.Eine Basis heißt orthogonal, wenn Sind die Basisvektoren normiert, d., aus Vektoren für die gilt: \begin .Orthonormalbasis bestimmen., bn] orthogonal: i≠j⇒〈bi, bj〉 = 0. Compute answers using Wolfram’s breakthrough .

Orthonormalbasis

We’ll explore this and other uses of orthogonal bases in this section.Bestimmen Sie eine Basis zum orthogonalen Komplement U⊥.Orthogonale Matrix: Quadratische Matrix, bei der das Produkt der Matrix und ihrer Transponierten die Einheitsmatrix ergibt. Interaktive Aufgabe 172: Orthogonale Ergänzung, Koeffizientenbestimmung bezüglich einer Orthogonalbasis (2 Varianten) Interaktive Aufgabe 380: Winkel zwischen zwei Vektoren, Bestimmung eines orthogonalen Vektors .Eine Orthonormalbasis in einem Vektorraum ist eine Menge von Vektoren, die sowohl orthogonal (senkrecht zueinander) sind als auch eine Norm (Länge) von 1 haben. c) Bestimmen Sie eine orthogonale Basis des \mathbb {R}^ {3} R3, die aus Eigenvektoren von A A besteht. Unendlichdimensionale Räume .Wenn u und v die Basis­vektoren eines Unterraums U sind, so lassen sich aus ihnen auf diese Weise zwei orthogonale Basis­vektoren u und v‘ konstruieren. Die Vektoren dürfen untereinander also kein anderes Skalarprodukt besitzen, sonst sind diese nicht orthogonal zu einander. Danke schön für die Hilfe Vektoren x, y sind orthogonal , falls 〈x, y〉 = 0. eine unitäre Matrix.

• Original Fußmatten Für Mercedes
• Orientation Leo Deutsch , orientation light
• Osiander Hallstadt , Osiandersche Buchhandlung Hallstadt
• Orthopädie Leipzig Johannisplatz
• Orthopädie Mallorca Team , ORTHO-TEAM Basel
• Ortsamt Rostock Groß Klein – Onlinedienste Rostock: Amtliche Meldebestätigung ausstellen
• Organischer Rasendünger Testsieger
• Orthopäde Pruchhorst Aufzug , Orthopädische Praxis Hamm
• Orphan 2009 Summary : Orphan (2009 film)
• Organizing Notebooks For Work , Todoist