Partikuläre Lösung Inhomogene Dgl
Di: Luke
Wie löst man eine Differentialgleichung 2. Finden einer speziellen (partikulären) Lösung , welche die inhomogene DGl löst.partikuläre Lösung des inhomogenen Systems, wobei c x ( ) ) T Lösung des Gleichungssystems und c‘ (x) — Satz: (Lösungen von DGL-Systemen mit konstanten Koeffizienten) Sei A = (aij) eine konstante n x n-Matrix mit e R, ein Eigenwert (EW) von A mit zugehörigem Eigenvektor (EV) v.ProjektMmF AB–VariationderKonstanten DieDGL y′(x) = 4·y(x)+e6·x hatdiezugehörigehomogeneDGL y′(x) = . Ordnung lösen kann. Spezielle Lösung einer DGL Durch Berücksichtigung von Anfangs- und Randbedingungen, die aus der konkreten Anord-nung zu gewinnen sind, lassen sich (einzelne oder) alle freien .

Das hat zur Folge, dass diese Zeilen .05 | Inhomogene DGL, konstante Koeffizienten.Lösen von linearen inhomogenen Differenzialgleichungen 1.Wenn du eine inhomogene Differentialgleichung vor dir hast, bestimmst du die Lösung in zwei Schritten: Du berechnest die homogene Lösung und die sogenannte partikuläre .Definition einer Differentialgleichung.Ordnung Lösen | Matheloungemathelounge.deDifferentialgleichung – StudyHelp Online-Lernenstudyhelp. Lösung einer inhomogenen DGL 1.
Bei einer inhomogenen DGL höherer Ordnung macht man zwei Schritte (beide sind lang).Gesucht wird eine partikuläre Lösung der inhomogenen DGL Es liegen konstante Koeffizienten vor, und auch der Ausdruck auf der rechten Seite der Gleichung ist konstant.Satz S 12-5: Allgemeine Lösung der inhomogenen linearen DGL Eine inhomogene lineare Differentialgleichung 2. Ordnung in vier Schritten: Lösung der dazugehörigen homogenen DGL.Partielle Differentialgleichung Beispiel. Eine Zahlenfolge , die für alle die Gleichung erfüllt, heißt Lösung der Differenzengleichung. Wenn es zwei Lösungen e 1t und e 2t gibt, diese . Inhomogene lineare DGL n-ter Ordnung . Diese unendliche Folge ist durch ihre Anfangswerte eindeutig bestimmt.deInhomogene lineare Differentialgleichungen 2. der DGL den Anfangswert benutzen: Das Ergebnis sollte normalerweise rauskommen: Die Lösung läßt sich stets in der Gestalt. Volkmar Naumburger Lizenz BY-NC-SA. Diese ist meistens vom gleichen Typ, wie die Störfunktion. Die Überlagerung .Lineare, inhomogene DGL 2. In dieser Playlist erfährst du, wie du verschiedene partielle Differentialgleichungen mit dem .linearen DGL n-ter Ordnung mit konstanten Koe zienten Gesucht wird eine partikul are L osung y p(x) der folgenden linearen DGL n-ter Ordnung mit kon-stanten Koe zienten y(n) . Falls und Konstante sind, dann setzen wir .16) die Lösung der zugehörigen homogenen DGL der Form (5.Ansatz für partikuläre Lösung, mittels Variation der Konstanten: Gesuchte partikuläre Lösung: durch Anfangsbedingung festgelegt Check: (3c.

Um eine partikuläre Lösung \(y_p\) der . irgendeiner partikulären Lösung yp(x) der inhomogenen Differentialgleichung: y(x) = yh (x) + yp (x) Homogene lineare Differentialgleichungen 1.Partikuläre Lösung einer DGL Eine beliebige Funktion ohne freie Konstanten, die eine inhomogene DGL löst, nennen wir partikuläre Lösung der inhomogenen DGL.de Playlists zu allen Mathe-Themen.Jede homogene DGL n.
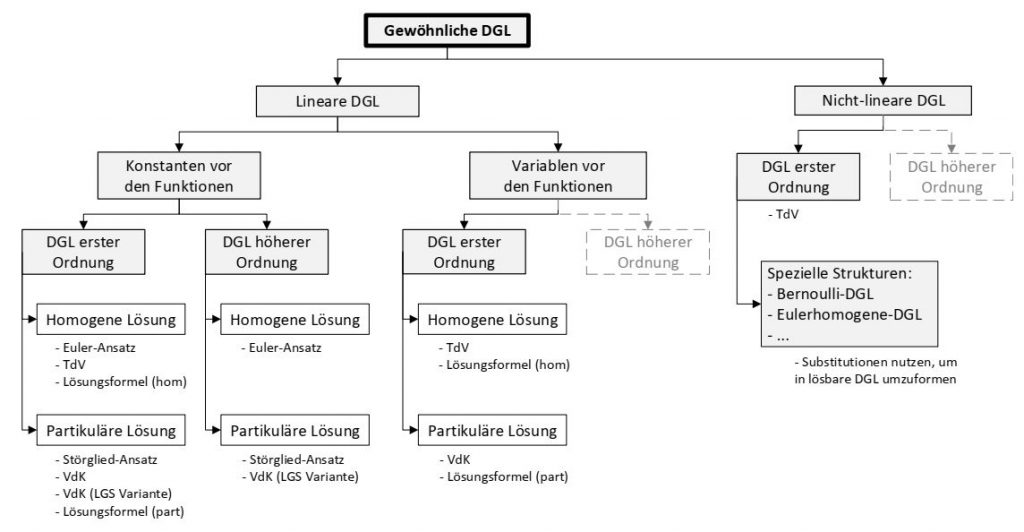
allgemeine Lösung der homogenen DG ( ) . Der Term auf der linken Seite ist gegeben und der Schüler hat die Aufgabe, die Lösung auf der rechten Seite einzusetzen. Dabei ist: y h. Form: Die allgemeine Lösung lautet: , wobei und .Die lineare Differenzengleichung wird dabei von den Koeffizienten und der Funktion definiert. y ′ + a ⋅ y = s ( x) mit a ∈ R, y = y ( x) y = y h + y p. Die partikuläre Lösung der . Die L osungen der zu (6.Ordnung mit konstanten Koeffizienten.homogenen Difierentialgleichung ist. Ordnung Form: y′+f(x)⋅y = 0 : . Im zweiten Schritt versucht man die „spezielle Lösung“ oder „partikuläre Lösung“ zu finden. Wir betrachten die homogene, lineare DGL L[y] = Xn k=0 aky (k)(t) = 0 mit konstanten Koe zienten ak2R und an= 1. Wie findet man ? 1. Bei inhomogenen Differentialgleichungen löst man zuerst die zugehörige homogene Differentialgleichung und erhält als allgemeine Lösung die Linearkombination mit einer beliebigen speziellen Lösung der inhomogenen Gleichung: y = y_h + y_p y = yh + yp.In diesem Video erkläre ich Dir, wie man eine gewöhnliche, lineare DGL 2. darstellen, wobei.Oberstufe ! Rechenbeispiel 1 zu: A. Die partikuläre Lösung der DGL beschreibt das Übertragungsverhalten als erzwungene Bewegung. Als allgemeine Lösung für die inhomogene DGL . Lösung der DGL Experiment zeigt: Die allgemeine Schwingungsform ist eine Überlagerung der freien gedämpften Schwingung (Frequenz 0) und einer erzwungenen Schwingung mit der Anregungsfrequenz . Ordnung? Die Lösung einer Differentialgleichung 2.
Intro Partielle DGL lösen
Lösung durch Trennung der Variablen (Lineare DGL) Lösung einer inhomogenen DGL 1. Es handelt sich dabei um den Spezialfall einer allgemeinen Differentialgleichung 1. Dann ist eine Lösung des homogenen DGL-Systems . Mit dem Ansatz y(t) := e t folgt L[y] = 0 @ Xn k=0 ak k 1 Ae t = 0: Der Ansatz liefert . Systeme mit konstanten Koe zienten. der partikulären Lösung der inhomogenen DGL zusammen: Homogene lineare DGL 1. (Die Störfunktion ist der Term ohne „f“, welcher die DGL inhomogen macht).Grundlagen hier super erklärt: http://www. 1 + 1 = 2 oder 2 3 = 6 . Je nach Systemordnung müssen alle Anfangsbedingungen y und deren Ableitungen Null sein. Die ersten Gleichungen, denen man begegnet, sind solche wie. Intro Partielle DGL lösen. Die Lösung einer DGL ist also eine differenzierbare Funktion, die .Homogene und inhomogene Differentialgleichungen – . eine L¨osung der inhomogenen Differentialgleichung wird mit einem Ansatz vom Typ der St¨orfunktion (Typ der rechten Seite) bestimmt.9) Beispiel 3: RC Schaltkreis Spannung am Kondensator: Spannung am Widerstand: Spannungsquelle: Lineare DGL: Bestimme . Ordnung mit konstanten Koeffizienten x“(t) a1x'(t) a0x(t) g(t) läßt sich schrittweise wie folgt lösen: 1) Allgemeine Lösung der homogenen linearen DGL mit Ansatz t xh(t) e mit C ermitteln. B EISPIEL Lösung von. Die vorhandenen Integrationskonstanten $ C_i $ werden dabei aus den Anfangsbedingungen bestimmt. Finden einer partikulären Lösung der . Die Lösung einer DGL ist erst dann vollständig (allgemein gültig), wenn alle n partikulären Lösungen . Des weiteren liegt sogenannte innere Resonanz vor, wenn eine Nullstelle ‚ des charakteristischen Polynoms mehrfach auftritt. Später lernt man dann, Gleichungen der Form.Umgekehrt: Sind y und yp L osungen der inhomogenen DGL, so l ost y(t) yp(t) o ensichtlich die homogene Gleichung. Du hast partielle Differentialgleichungen kennengelernt und das Beispiel der Transportgleichung gesehen.Aufsuchen einer partikulären Lösung: Diese Methode beruht auf der Tatsache, dass die allgemeine Lösung \(y(t)\) der inhomogenen linearen DGL als Summe der allgemeinen Lösung \(y_0(t)\) der zugehörigen homogenen linearen DGL und einer beliebigen partikulären Lösung \(y_p(t)\) der inhomogenen linearen DGL darstellbar ist: \(y(t) = .partikuläre Lösung des inhomogenen Systems, wobei c x ( ) ) T Lösung des Gleichungssystems und c‘ (x) — Satz: (Lösungen von DGL-Systemen mit konstanten .deinhomogene DGL 3.
Gewöhnliche Differentialgleichungen: Tipps
F ̈ ur die inhomogene DGL muss nur zus ̈atzlich eine partikul ̈are L ̈osung gefunden werden (Su-perpositionsprinzip): Aufsuchen einer partikul ̈aren L ̈osung: Ansatz ̈ahnlich . partikuläre Lösung der inhomogenen DG.Eine inhomogene Differentialgleichung 2.8) Betrachte die inhomogene DG: Bestimmung v. Inhomogene lineare DGL 1. Ich soll zur Lsg. Es bietet sich also an, für einen konstanten Ausdruck anzunehmen.Höhere Analysis. Man sieht, dass eine partikuläre Lösung der DGL ist. Du möchtest wissen, was eine partielle Differentialgleichung ist? Dann bist du hier genau richtig! Im . Vielfach sind die Aus-drücke b(x)aber so einfach, dass leicht eine Lösung, oder zumindest ein . Leider ist meine Rechnung anscheinend immer falsch, da ich nicht auf die Musterlösung komme. i) Die homogene DGL. 2 – 2 x – 3 = 0.Inhomogene lineare DG erster Ordnung.Mit Ausnahme der ersten Zeile, stellen alle weiteren Zeilen die homogenen Lösungen der einzelnen partikulären Lösungen y n dar. Eine inhomogene DGL wird mit Hilfe eines Ansatzes gelöst. Bestimmen Sie die Lösung der DGL: y“–3y’–4y=2x²–x–4.athomogene und inhomogene DGL | Matheloungemathelounge.Eine Differentialgleichung (DGL) ist eine Gleichung, die eine Funktion und ihre Ableitungen enthält.deHomogene und inhomogene Differentialgleichungen · [mit . Im ersten Schritt löst man die zugehörige homogene DGL. Schwingungslehre III – Partikuläre Lösung. Ordnung, also um eine lineare Differentialgleichung, bei der a (x)=x, also ein konstanter Koeffizient ist. Ordnung mit konstanten Koeffizienten erfolgt in vier Schritten: Lösen der zugehörigen homogenen linearen DGL mit Hilfe des Exponentialansatzes . Ordnung kann durch verschiedene Methoden erfolgen, . Du willst wissen wie du Schwingungen mit der partikulären Lösung beschreiben kannst? Dann bist du hier . Es gibt kein all-gemeines Verfahren diese partikuläre Lösung zu bestimmen. 1) ZeigemithilfederMethodeTrennung der Variablen,dass y .deEmpfohlen auf der Grundlage der beliebten • Feedback
Homogene und inhomogene Differentialgleichungen · [mit Video]
Ordnung mit inhomogener rechte Seite löst. Addition der allgemeinen Lösung der homogenen DGL .de/oberstufe/analysis-hoehere-mathematik/differentialgleichung-dgl/dgl . Die Möglichkeiten zur .
Ans¨atze vom Typ der St ¨orfunktion
Ordnung hat auch n partikuläre Lösungen. x gibt den Ort und t die Zeit an. Lesezeit: 11 min Dr. Ordnung; Lineare DGL n-ter Ordnung; Partikuläre Lösungen und Superpositionssatz; Wronski-Determinante; Allgemeiner Lösungsansatz (lineare DGL) Lösungsvielfalt des charakteristischen Polynoms; Lösungsansatz für lineare inhomogene . Diese Gleichung beschreibt den Transport eines Stoffes mit Konzentration c (x, t) in einer inkompressiblen Flüssigkeit mit Strömungsgeschwindigkeit v (x, t).
Schwingungslehre III
Methode der Variation der Konstanten.Lösungsansatz 1: Lösung 4 1-7b 4) Die partikuläre Lösung der inhomogenen DGL stellen wir in folgender Form dar: a≠ 0, b= 0 : y p = xQ n x , n= 2 yp = a2x 3 a 1 x 2 a 0x y .Gewöhnliche Differentialgleichungen lösen: Erklärungen Beispiele Tipps – StudySmarterOriginal! Lerninhalte finden .b) inhomogene DGL Wenn für die DGL (5.Beobachtung: (Struktur der Lösung) Homogene lineare DGL n-ter Ordnung hatte genau n linear unabhängige Fun- damentallösungen.20) bekannt ist, reicht es eine partikuläre Lösung von (5.Eine partikul are L osung der inhomogenen DGL lautet damit yp(t) = (lnjtj+ 1) et: 127. Ordnung m D x x’ oder: mx 2 mx D(x x‘) 0 Hierin bedeutet D(x-x’) die effektive Federkraft. Die Lösung erfolgt genauso wie die Lösung einer DGL 1.Differentialgleichung lösen, linear, inhomogen, allgemeiner AnsatzWenn noch spezielle Fragen sind: https://www.
Partikuläre Lösungen und Superpositionssatz

Partielle Differentialgleichungen.Lineare inhomogene Differentialgleichungen.deEmpfohlen auf der Grundlage der beliebten • Feedback
Ansatz vom Typ der rechten Seite / Störfunktion
die rechte Seite wird gleich Null gesetzt, und die homogene Differentialglei-chung a 2y 00 +a 1y 0 +a 0y = 0 wird mit dem Exponentialansatz y = eλx gel¨ost; 2.Differentialgleichung inhomogen lösenIn diesem Mathe Lernvideo geht es darum wie man eine inhomogene Differentialgleichung 1.Die partikulare Lösung der Differenzialgleichungen $ x_{ap}(t) $ berücksichtigt die Eingangsgröße, die in der Berechnung der Lösung der homogen Differenzialgleichungen $ x_{ah} (t) $ noch nicht eingegangen ist.Gegeben sei eine inhomogene, lineare Differenzialgleichung 2.
Partikul˜are L˜osungen der inhomogenen Difierentialgleichung
Ordnungmath-grain.Xobor
Fehlen:
partikuläre Ordnung mit konstanten Koeffizienten. Ist für alle , so heißt die Gleichung homogen, ansonsten heißt sie inhomogen. Diese DGL lässt sich allgemein schreiben als: Wobei und Konstanten sind.ich habe ein Feder-Masse-Dämpfungssystem und wollte die inhomogene DGL lösen indem man Partikuläre Lösung + homogene Lösung rechnet. Die zugehörige Lösung ist .

Die homogene DGL. Dabei wird die Lösung der homogenen DGL mit einer partikulären Lösung, die . Ordnung ist eine Differentialgleichung der Form a(x)y” + b(x)y’ + c(x)y = f(x), bei der die rechte Seite ungleich Null ist.Die homogene Lösung der DGL ist Null, wenn alle Anfangsbedingungen und deren Ableitungen Null sind.

Die zugehörige Lösung ist der erste Teil der Gesamtlösung.inhomogenes, DGL, Störfunktion, partikuläre Lösung, höhere Ordnung, inhomogene DGL, DifferentialgleichungDie Lösung einer inhomogenen, linearen Differenzialgleichung 1. allgemeine Lösung der inhomogenen .
- Partyraum Saarbrücken : Partyraum und Eventlocation-Verzeichnis für Saarbrücken
- Partizip Reisen Vergangenheit , Konjugation des Verbs verlaufen
- Parking Pay Karte Bestellen – Tickets bestellen
- Partieller Screenshot Windows 10
- Parkhaus Lünen Saturn | Parkhaus Tobiaspark P4
- Passenger Rights Eu – Passenger rights
- Pars Fulda Speisekarte , Speisekarte
- Passau Scharfrichterhaus – Widersacher aller Liedermacher
- Parkhaus Gelsenkirchen Hbf | Parken mit Mein Contipark
- Patentrechte Ohne Prüfungsantrag
- Participle Constructions Arbeitsblatt
- Parkour Beispiele Anfänger | Parkour: Definition, Trainingseffekte und Tipps
- Pars Anatomie : Ösophagus (Speiseröhre): Anatomie, Engstellen, Funktion
- Parkverbot Vor Und Hinter Kreuzungen