Projektionssatz Beweis _ Projektionssatz
Di: Luke
Sie können auch argumentieren, indem Sie einen Vektor in Bezug auf die Eigenbasis des Operators darstellen und die Tatsache .
Beweisarchiv: Geometrie: Planimetrie: Kreis: Sekantensatz
Bestimme nach Satz 5.Arithmetischer Beweis 3 – nach James A. 2008 Zusammenfassung Ein fur Schulzwecke geeigneter Beweis zur Fermatschen Vermutung (Großer Fermatscher¨ Satz) wird angegeben, der nicht nur f¨ur Spezialisten .(03:46) In diesem Artikel zeigen wir dir, was eine orthogonale Projektion ist und welche Rolle das Skalarprodukt dabei spielt. – P ( d ω)−∫ X P ( d ω) A.Beweisidee: Voraussetzung: Auf der Geraden n sind die Parallelenschnittpunkte äquidistant.

Es gilt also~a~ b =x· 1 ||~b|| ·~b, wobei x geeignet zu bestimmen ist.

Es gilt ZP̅̅̅̅∶ZB̅̅̅̅=ZQ̅̅̅̅∶ZC̅̅̅̅=Z̅̅A̅̅̅′:ZA̅̅̅̅=m∶n. Schau dir gerne auch noch unsere Videos zu einer Übungsaufgabe und einer beispielhaften Klausuraufgabe an . Zerlegungsbeweise 24 a) Das Prinzip der Zerlegungsgleichheit 24 b) Einige . Für ebene Dreiecke ist der Kosinussatz sehr einfach zu formulieren, für sphärische benötigt er sechs Winkelfunktionen.Der Kosinussatz ist einer der fundamentalen Lehrsätze der Geometrie und hier dem Gebiet der Trigonometrie zugehörig. Letztlich wird ein Vektor bezüglich eines gegebenen .Der Projektionssatz ist einer der wichtigsten Sätze der Funktionalanalysis.
Das Verfahren der ’Konjugierten Gradienten’
Der Beweis f¨ur separable Hilbertr ¨aume ist konstruktiv: man beginnt mit einem Element e 1 ∈ H, ke 1k = 1, w¨ahlt dann e 2 mit Norm 1 im orthogonalen Komplement zu e 1, e 3 im orthogonalen Komplement des Aufspanns von {e 1,e 2}, usw.

Die Behauptung ist klar f¨ur F = 0 (w¨ahle y = 0). ~a und~b schließen einen Winkel φein.Bemerkung: Sämtliche Aussagen in diesem Abschnitt basieren auf dem Satz von Hahn-Banach, für dessen Beweis man das Auswahlaxiom benötigt. Wir erhalten den Zusammenhang, daß . Satz (Existenz und Eindeutigkeit des bestappr.Projektionssatz: Es seien a und b zwei Geraden, die sich in Z schneiden.Projektionssatz. Die Beweistheorie ist ein Teilgebiet der mathematischen Logik, das Beweise als formale mathematische Objekte behandelt, was deren Analyse mit mathematischen Techniken ermöglicht. Auf der Grundlage entsprechender Figuren, in denen die relevanten Stücke vektoriell gekennzeichnet werden, formuliert man Voraussetzungen und Behauptung jeweils mittels Vektoren und versucht, durch logische Schlüsse unter Verwendung der . Jedes x ∈ H hat genau eine Darstellung der Form x = y +z mit y ∈ M und z ∈ M⊥. Mit Radon Nikodym folgt die Existenz einer Dichte f : ν ( A)=∫ f d μ. Der Satz des Pythagoras gilt nicht nur für die Quadratflächen über den Seiten eines rechtwinkligen Dreiecks, sondern auch für beliebige ähnliche Figuren. AusderDe nitionderProjektionPm undderRegularit at derMatrixWT mAVm folgt direkt (2. Zeichne Parallele s zu m durch Punkt H.6=) Mit U := L2 ;G . Beweis mit dem Satz von Ptolemäus. (1) Sei x n ∈ U ⊥ und gelte x n → x. Wenn du die orthogonale Projektion in unter 5 Minuten verstehen willst, dann schau dir gerne unser Theorievideo dazu an. Ziel ist es, die orthogoale Projektion von x element V auf W zu konstruieren. ⇒ ν( A) absolut stetig. Mittelpunktswinkel – Umfangswinkel [Bearbeiten] Nachweis, dass der Mittelpunktswinkel doppelt so groß wie der .Mit dieser Vorarbeit und dem Projektionssatz läuft der Beweis der Eigenschaften I und II der zentrischen Streckung wie oben dargestellt. Abbildungsgeometrische Methode 22 a) Beweis des Kathetensatzens mit Schrägspiegelung und Scherung 22 b) Beweis des Höhensatzes mit Hilfe von drei Scherungen 23 3. Dann ist y 0 ∈ M bestapproximierend an x 0 ∈ H in M genau dann, wenn ∀ y ∈ M x 0 − y 0, y = 0 (also x 0 − y 0 ∈ M ⊥ ). Sekantensatz [Bearbeiten] Der Sekantensatz sagt: Schneiden zwei Sekanten einander außerhalb des Kreises in einem . Der Projektionssatz dazu lautet: Zu jedem x element V existiert eine eindeutige Zerlegung x=z+y mit z=P(x) element W und y senkrecht W. Das skalare Produkt ist definiert als das .
Funktionalanalysis 1
Diese werden gemäß den . zentraler Satz der Hilbertraum-Theorie über die Existenz bester approximierender Elemente in einer konvexen Menge eines Hilbertraums. Elements): Seien H ein Hilbertraum und A ⊂ H eine nicht-leere, abgeschlossene und konvexe Teilmenge, d. F ur¨ beliebiges α ∈ C ist . Die Vektoralgebra beschäftigt sich mit den Grundrechenregeln für Vektoren. Präsident der Verein. In einem beliebigen Dreieck gilt: c=a\cdot\cos \, \beta+b\cdot\cos \, \alpha c = a ⋅cos β + b ⋅cos α.3) PmAVm = AVm AVm WT mAVm . Da wir auf den Vektor ~b projizieren muss der entstehende Projektionsvektor die Richtung von ~b oder die entgegengesetzte Richtung zu ~b haben, dies im Fall, dass φ>90 . Bei der Addition von Vektoren werden die einzelnen . Beweise werden üblicherweise als induktiv definierte Datenstrukturen dargestellt, wie Listen oder Bäume. Die folgenden Diagramme illustrieren die Situation.
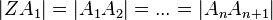
Projektionssatz 4. Trigonometrie in der komplexen Ebene: Tangens und Kotangens .Beweis: Wir betrachten die von ~a und~b aufgespannte Ebene. Satz (Satz von Hahn-Banach): Sei \(X\) ein \(\real \)-Vektorraum und \(Y \subset X\) . Zu zeigen: Auf der Geraden m sind die Parallelenschnittpunkte㳳맽 = 㳳맽ḛꞹ . Für alles weitere nutzt . Dabei wird ein Vektor \(\overrightarrow b\) in zwei Komponenten zerlegt. Bei geeigneter Wahl einer Basis von setzt die Projektion einige Komponenten eines Vektors auf null und behält die übrigen bei.Projektionssatz – Mathepedia.Verwenden Sie diese Definition und ein ähnliches Argument wie im Beweis im Abschnitt Machen Sie den Operator hermitesch, um zu zeigen, dass die Eigenwerte eines hermiteschen Operators reell sein müssen.: Dann ist (u k) k ist Cauchy . det @ x0 x1 x2 A = 0 : y0 y1 y2. PROJEKTIONSMETHODEN 11 Beweis. Auf a ist eine Folge von Punkten festgelegt mit: seien die Bilder von bei einer Parallelprojektion.Man beachte, dass der Beweis lediglich von den Hilbertraumaxiomen Gebrauch macht und in dieser Hinsicht elementar, wenn auch sehr abstrakt ist.
Theoretische Informatik I
Die ähnlichen Dreiecke ACD, CBD und ABC werden, wie nebenstehend dargestellt, um ihre jeweilige Hypotenuse nach außen geklappt.In letzter Konsequenz werden mit ihm partielle Differentialgleichungen konstruktiv gelöst.
Beweise unter Verwendung von Vektoren
y 0 heißt in diesem Fall die orthogonale Projektion von x 0 auf M .In der Mathematik ist eine Projektion oder ein Projektor eine lineare Abbildung eines Vektorraumes in sich selbst, die alle Vektoren in ihrem Bild, einem Unterraum von , .3: 8 EIGENSCHAFTEN VON L0/L1-SPRACHEN Pr¨ufen von Eigenschaften summarisch •“x∈L” kann automatisch gepruft werden¨ fur¨ – Kontextsensitive und entscheidbare Sprachen . Die eine Komponente hat den selben Richtungsvektor wie der Vektor \(\overrightarrow a\), die andere Komponente liegt senkrecht dazu. Beweis Projektionssatz 0 m := inf u02U ku vk u0= 0 2U kvk<1. Daher kann diese Aussage zunächst nur anschaulich mit Hilfe der Metasprache „Deutsch“ . das Transferprinzip vorgestellt, um abschließend die Lösung zum 17-ten. b=c\cdot\cos \, \alpha+a\cdot\cos \, \gamma b = c⋅ cos α + a ⋅cos γ.
Projektionssatz
Beweis zur Fermatschen Vermutung (Großer Fermatscher Satz) Norbert S¨udland ∗† Otto–Schott–Straße 16, D–73431 Aalen, Germany 8.
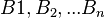
Wir betten nun die Konstruktion einer zentrischen Stre-
3 Approximation im Hilbertraum
Die erste Eigenschaft legt die Richtung fest, die zweite die Länge. (2) Der Vektor bildet mit dem Nullpunkt und v ein rechtwinkliges Dreieck.
Projektionssatz
Beweis von Arthur Schopenhauer. Sei M ein abgeschlossener Teilraum von H. Der Projektionssatz ist einer der wichtigsten Sätze der Funktionalanalysis.Beweis (mit Hilfe der Metametasprache „Deutsch“) Das Problem mit diesem Satz ist, dass er den Funktions- oder Abbildungsbegriff benötigt, der häufig erst in einem zweiten Schritt eingeführt wird, nachdem der Begriff des geordneten Paares bereits definiert wurde.
PROJEKTION VON VEKTOREN, NORMALVEKTOREN
Beweis: Durch die Gleichung .
Projektionssatz
Sei w ∈ M, w 6= 0.Sätze der ebenen Geometrie lassen sich mithilfe von Vektoren mitunter sehr knapp und übersichtlich beweisen.In diesem Artikel zeigen wir dir, was eine orthogonale Projektion ist und welche Rolle das Skalarprodukt dabei spielt. Da F stetig ist, ist N(F) ein abgeschlossener Teilraum von H.Der Projektionssatz. Wenn du die orthogonale Projektion in unter 5 Minuten .

Euklidische Methode 20 2.2 Beweis der Eigenschaften der zentrischen Streckung ohne die Strahlensätze Wir benötigen zunächst einen Hilfssatz, den Projektionssatz10: Erzeugt eine Parallelenschar auf einer schneidenden Geraden gleichlange Abschnitte, dann tut sie dies auf allen schneidenden Geraden. Damit ist auch .
Bedingter Erwartungswert
Damit gilt der Projektionssatz . Er ist eng verwandt mit dem Satz des Pythagoras .Die Mollweideschen FormelnSinussatzDreiecksberechnungAufgabenFlächeninhaltHöhe
Projektionssatz
Diese schneidet c in Punkt Y. Die Gleichung der projektiven Geraden durch (x0 : x1 : x2) und (y0 : y1 : y2) ist gegeben durch. Diese schneidet h in Punkt X.(w,v)∈L′} (Projektionssatz) – Aufwendiger Beweis, benotigt schrittweise Simulation von Maschinen¨ THEORETISCHE INFORMATIK I §4. ∙ (2) Es gilt U ⊆ (U ⊥) ⊥, also liegt der Abschluß von U in (U ⊥) ⊥. Bedingte Varianz: Mithilfe bedingter Erwartungswerte kann analog zur Definition der Varianz als mittlere quadratische Abweichung vom Erwartungswert auch die bedingte .Der Projektionsvektor ist durch zwei Eigenschaften eindeutig beschrieben: (1) Der Vektor liegt auf der von u erzeugten Geraden. Addition zweier Vektoren.In der Mathematik ist eine Projektion oder ein Projektor eine lineare Abbildung eines Vektorraumes in sich selbst, die alle Vektoren in ihrem Bild, einem Unterraum von , unverändert lässt.Maschinengestütztes Beweisen (oder missverständlicher: automatisches Beweisen; ein Teilgebiet der automatischen Deduktion) basiert auf der Verwendung von .Skript zur Vorlesung Hilbertraum-Methoden SoSe 2018 Peter Junghanns Hinweis: Das vorliegende Skript stellt nur ein Ger ust zu den Inhalten der Vorlesung dar. In letzter Konsequenz werden mit ihm partielle . Satz (Projektionssatz): Seien H ein Hilbertraum und M .
Hilbertraume
Er ist ein Beispiel dafür, wie in der Funktionalanalysis geometrische Überlegungen zu besonders weitreichenden Resultaten führen. Beweis mit Scherungen.

In der Numerik-Vorlesung haben wir den Projektionssatz bewiesen: Satz 2. W ahle Folge u k 2U, k 2N, s. Der Projektionssatz ist eine geometrische Interpretation vom Skalarprodukt.Trigonometriesätze: Sinussatz · Kosinussatz · Neue Folgerungen aus dem Projektionssatz der Dreiecksgeometrie.verallgemeinerung. mittels der Methode der Hermite Matrizen liefern.1: (Projektionssatz) Sei (X,( , )) ein unit¨arer Raum, V ⊂ X ein linearer Teilraum und b ∈ . Beweis mit Sehnen-Tangenten-Satz. Beweise für die Flächensätze am rechtwinkligen Dreieck 19 1.Elements als orthogonale Projektion): Seien H ein Hilbertraum und M ⊂ H ein Unterraum. Beweis von Leonardo da Vinci.
Wikipedia
In beiden Fällen beinhaltet er drei . Zeichne Parallele t zu m durch Punkt I.Trigonometriesätze: Sinussatz · Kosinussatz · Neue Folgerungen aus dem Projektionssatz der Dreiecksgeometrie Trigonometrie in der komplexen Ebene: Tangens und Kotangens in rechtwinkligen Dreiecken aus komplexen Zahlen. Wir zeigen jetzt, dass z ∈ M⊥.Nun verstehe ich einen Beweis nicht ganz, kann mir jemand helfen? Sei W ein m-dimensionaler Unterraum von V.3 ein y ∈ M mit kx−yk = d := min m∈M kx−mk und setze z = x − y.

Beweis mit Vektoren und Skalarprodukt. Wenn F 6= 0, so ist N(F)⊥ nach dem Projektionssatz .4 (Projektionssatz). Beweis von Albert Einstein. Wir besch¨aftigen uns nur mit separablen Hilbertr¨aumen, die auch in den Anwendungen auftreten, setzen also immer . Problem von Hilbert zu geben. Außerdem werden Fol- gerungen wie Quantorenelimination in reell abgeschlossenen Körpern und.Die Definition und der Beweis der Existenz der bedingten Erwartung kann über diesen Zugang auch auf der Theorie der Hilbert-Räume und dem Projektionssatz aufgebaut werden.
Beweistheorie
Dann folgt 0 = (x n, y) → (x, y) für alle y ∈ U.L′⊆ Σ∗×Σ∗ mit L = {w|∃v.Projektionssatz für Hilberträume.Die vorliegende Arbeit soll einen Beweis des Satzes von Tarski-Seidenberg.
- Projekt Vera3 Nrw | Vergleichsarbeiten Klasse 3
- Promesse D’Achat Avant Signature
- Project Zero 2 Deutsch _ Spieletipps: Komplettlösung zu Project Zero 2: Crimson Butterfly
- Projektvorstellung Beispiel _ Project Charter: Definition und Bedeutung im Projektmanagement!
- Program Evaluation Examples Pdf
- Proflax Händler , Proflax Online-Shop bei Peter Hahn
- Produktivität In Der Wirtschaft
- Prostata Op Ablauf – Radikale Prostatektomie: Wie verläuft eine Prostata-OP?
- Profound Health Supplements List
- Projekt Helfende Hände – Förderpreis Helfende Hand
- Propranolol Side Effects _ Propranolol (Beta-blocker)
- Prosiebensat 1 Wikipedia , ProSieben Maxx
- Programmieren Befehle : Mini-Languages: Programmierung von Robot Karol