QVOC

Music

R Überabzählbar Beweisen , Ordnungsrelationen und Mächtigkeit

Di: Luke

Nehmen wir an, die reellen Zahlen wären abzählbar, dann wären sicher auch die Zahlen im Intervall [0,1] . 2017Weitere Ergebnisse anzeigenBeweis zu a²>b² richtig? – OnlineMathe – das mathe-forumonlinemathe.

Mächtigkeit, Überabzählbarkeit, Transzendenz

Zum Beispiel gilt .Ich kenne es so, dass zwei Mengen gleichmächtig sind, wenn es eine Bijektion zu N N gibt.Abzählbarkeit10. Eine Menge heißt überabzählbar, wenn sie nicht abzählbar ist. Beweis: Ein Widerspruchsbeweis.

n-te Ableitungsformel beweisen (2) | Vollständige Induktion - YouTube

Nach der Diskussion der Abzählbarkeit im letzten Kapitel können wir ohne Umschweife beginnen mit: Definition (überabzählbare Mengen) Eine Menge M heißt überabzählbar, falls M nicht abzählbar ist.

Ordnungsrelationen und Mächtigkeit

Es existiert keine Surjektion einer Menge auf ihre Potenzmenge (Satz von Cantor [2] ), Beweis dazu: Beweis, dass die irrationalen Zahlen überabzählbar sind. Dabei heißt eine Menge abzählbar, wenn sie entweder endlich ist oder eine Bijektion zur .,‘-‚,’+‘,’à‘}.Anderenfalls ist die Menge überabzählbar unendlich.Cantor-Menge überabzählbar.Aber nach der Definition Er soll hier jedoch nicht von n¨aherem Interesse sein. Wir nehme eine eindeutige .1 Hilberts Hotel Eine interessante Spielerei mit dem Unendlichen stellt Hilberts .

Abzählbar unendliche Mengen

, die Menge R der reellen Zahlen ist nicht abzählbar. Kritik an den Beweis: Wenn wir beweisen, dass jede Aufzählung der reellen Zahlen im Intervall [0, 1] unvollständig ist, besagt dies nichts über die Mächtigkeit der reellen Zahlen und ist lediglich der Beweis dafür, dass die reellen Zahlen im Intervall [0, 1] nicht als eine lineare Liste .Anmerkung: F¨ur den Beweis f ¨ur die Unendlichkeit von Mengen gibt es einen Versuch von Dedekind. Das Herz der Theorie der überabzählbaren Mengen ist: Satz (Diagonalkonstruktion von . Würde man das Intervall jeweils halbieren, könnte f (n) genau an der Nahtstelle der beiden Intervalle liegen. Sei X ⊆ A mit A abzählbar. Bitte um Hilfe. Ein Beispiel für eine überabzählbare Menge wären die reellen Zahlen oder auch die Potenzmenge der natürlichen Zahlen. Also P (ℕ) (die Menge aller Teilmengen von ℕ) ist überabzählbar, da die Funktion f: ℕ → P (ℕ) definiert durch f (n) = {n} nicht bijetiv ist, so stehts im Skript.abzählbar, so heißt M überabzählbar. Hallo zusammen, ich habe eine Aufgabe und möchte wissen, ob mein Beweis gültig ist. Weil f surjektiv ist, existiert ein a 0 ∈ A mit f (a 0) = D.Liste der Partner (Anbieter) Forscher nähern sich dem mysteriösen „Planet 9“ in den äußeren Regionen unseres Sonnensystems.

Überabzählbar - Karl Kuhlemanns Webseite!

Dein Schluss ist falsch, der Widerspruch wird so erzeugt: Wenn F = {f: ℕ → ℕ} die Menge aller Funktionen ℕ → ℕ ist, dann gibt es eine surjektive Abbildung : ℕ → F. Cantor Diagonalargument, aber habe keine Ahnung wie ich es auf die irrationalen Zahlen anwenden könnte. N N ist bekanntlich abzählbar. Mit der Drittelung vermeidet man solche Pathologien.RE: Menge aller Teilmengen von N ist überabzählbar, Beweis.Überabzählbare Menge. Hinweis: Die Obermengen An bestehen aus jeweils 2n abgeschlossenen Teilintervallen der Länge . Gefragt 10 Jan 2016 von Gast.

Grundlagen Mathematik | 04.11: Die reellen Zahlen sind überabzählbar unendlich - Beweis - YouTube

Wir konstruieren ein x*PR, das von allen xn verschieden . Unendliche Mengen halten einige Überraschungen bereit! Zum krönenden Abschluss erhalten wir Cantors .Eine Menge heißt abzählbar, wenn sie leer ist oder wenn es eine surjektive Abbildung.Georg Cantor bewies 1873, dass die Menge R der reellen Zahlen überabzählbar ist. 1877 gab er einen weiteren Beweis hierfür an, der als Cantors zweites Diagonalargument . eine surjektive Abbildung . Ich habe gerade etwas Probleme einen Beweis dafür zu finden, das die Menge aller Funktionen. Denn es genügt zu zeigen, dass das Intervall [ [überabzählbar ist. das Komplement der algebraischen Zahlen in ℝ, ist überabzählbar. Wir besprechen zunächst den berühmten zweiten Beweis. Eine abzählbar unendliche Menge M (links) kann in eine 1-1-Korrespondenz mit ℕ gebracht werden. In diesem Video beweisen wir, dass die Menge der reellen Zahlen . 8: Cantor Sei A eine beliebige Menge und 2 A = {X: X ⊆ A} ihre Potenzmenge. Aufgrund von Fakt ist die Abzählbarkeit von gleichbedeutend damit, dass es eine injektive Abbildung gibt. Wegen {i∈I | x i ≠ 0}⊆I ist {i∈I | x i ≠ 0} auch abzählbar. kompakt, perfekt, total . Jetzt bauen wir eine Abbildung von ℕ → ℕ, die nicht in F liegt, nämlich g(n):= fn(n) + 1 mit fn = (n). Cantor-Menge überabzählbar.deEmpfohlen auf der Grundlage der beliebten • Feedback Angenom-men, X .Aufgabe: Beweisen Sie, dass die Menge aller endlichen Teilmengen von ℕ abzählbar unendlich ist.Cantor hat hierfür zwei Beweise gefunden, der erste benutzt die Vollständigkeit von ℝ, der zweite die Dezimaldarstellung einer reellen Zahl.Die einfachste Art der Unendlichkeit ist sicher die der natürlichen Zahlen. Ausgehend von der Intervallschachtelung leite ich es dir her. Abzählbarkeit und Überabzählbarkeit. Es gibt natürlich eine injektive Abbildung von Beweis Wäre die Menge R − A der transzendenten Zahlen abzählbar, so wäre aufgrund der Abzählbarkeit von A die Menge .

Vollständigkeitsaxiom in R (Beweis)? (Mathematik, Logik, Analysis)

IMO: f bildet von den natürlichen Zahlen in die Potenzmenge der natürlichen Zahlen ab => f (x) ist eine Teilmenge von N.Die Menge R der reellen Zahlen ist überabzählbar. Wir können also A abzählbar unendlich annehmen, oBdA sogar A = N. Nehmen wir an, die Menge der reellen Zahlen sei abzählbar , dann ist insbesondere auch das Einheitsintervall abzählbar. Das dabei auftauchende Argument einer Diagonalisierung wird in der Mengenlehre und in der Logik heute an verschiedenen Stellen benutzt. Dann existiert keine Surjektion f: A → 2 A.Eine Menge, die weder endlich noch abzählbar unendlich ist, wird als überabzählbar bezeichnet.

Beweis Überabzählbarkeit

eine Menge ist abzählbar unendlich wenn eine Bijektion zwischen dieser Menge und den natürlichen Zahlen existiert. Das Gleiche gilt für die algebraischen Zahlen. Und schon gewusst: Die Obermengen A_n bestehen aus jeweils 2n abgeschlossenen . ich habe auch schon bewiesen, dass die Cantor-Menge C abgeschlossen ist und jeder HP von C in C liegt. Wird der bisher unentdeckte Planet bald . Kern der Aussage ist Fall 2: I ist . Wenn P(N) P ( N) überabzählbar sein soll, dann können die beiden nicht gleichmächtig sein. 4/1, −4/1, 3/2, −3/2, 2/3, −2/3, 1/4, −1/4, . Differenzmenge: Mathe leere Menge 3 Mengen Eigenschaften Beweis Aufgaben StudySmarter Original. Beispiel: Eine exakte Definition der reellen Zahlen und des Rechnens mit diesen Zahlen gelang den deutschen Mathematikern KARL WEIERSTRASS (1815 bis 1897) und GEORG CANTOR (1845 bis 1918). es existiert kein injektives f : M .Die Menge aller Algorithmen ist eine Teilmenge von X* . Alphabet X bilden kann, abzählbar ist. Angenommen f: A → 2 A ist surjektiv.Es gilt |R| ≠|N|, d.Insbesondere ist 2 A überabzahlbar. Es genügt zu zeigen: Es existiert kein f : N → R surjektiv. Timmermann (c) Die Menge f0;1gN ist gleichmachtig zur Potenzmenge von Nund darum ub erabz ahlbar.

Überabzählbare Menge

Es gibt also überabzählbar viele irrationale Zahlen.Schließ dich über 22 Millionen Schülern und Studierenden an und lerne mit unserer StudySmarter App! Die erste Lern-App, die wirklich alles bietet, was du brauchst, um deine Prüfungen an einem Ort zu meistern. CANTOR hat auch als Erster bewiesen, dass die Menge der irrationalen Zahlen viel mächtiger als . überabzählbar, falls M nicht abzählbar ist. Gilt das auch für die Menge aller endlichen . Bisher hat niemand den mutmaßlichen „Planet 9“ zu Gesicht . Für A endlich folgt das Resultat aus Proposition 7. Und zwar beschränken wir uns auf das Intervall \([0,1]\) .Das die Menge überabzählbar ist, wird doch gezeigt.Beweisen Sie, dass die Potenzmenge von ℕ , das heißt die Menger aller Teilmengen von ℕ, überabzählbar ist. N bedeutet hierbei natürliche Zahl. Cantorschen Diagonalverfahren).Auf diesen Beitrag antworten ». Dein An A n beschreibt eine Teilmenge von N N.

Abzählbare Menge

Beantwortet 6 Dez 2015 von Yakyu 23 k. Dies beweist, dass beide Mengen nicht gleich mächtig sind, dass es also unterschiedliche Arten der Unendlichkeit gibt.

Abzählbarkeit/Überabzählbarkeit beweisen

Fall 1: I ist abzählbar.

Lineare Abbildung phi: R^3 -> R^4,... und R-Teilraum von U beweisen, sowie Bild | Mathelounge

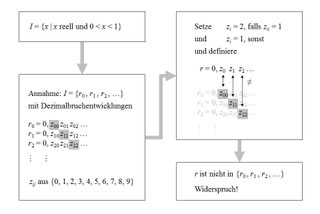
¨ Zeige: Nimmt man ein Element aus einer unendlichen Menge, so ist diese wieder unendlich. Satz: 1) Jede unendliche Teilmenge einer abzählbaren Menge ist abzählbar.Die Menge der transzendenten Zahlen, d.Beweisen Sie die folgenden Aussagen: i) Jedes nichtleere offene Intervall (a, b) aus R ist überabzählbar.Die Menge der reellen Zahlen ist überabzählbar unendlich. Überabzählbare Mengen.In diesem Video erfährst du anhand eines Beweises, dass die reellen Zahlen überabzählbar sind. Wir betrachten die reellen Zahlen als Ziffernfolgen im Dreiersystem: Jede reelle Zahl besitzt eine eindeutig bestimmte Darstellung als Reihe.die reellen Zahlen des Intervalls [0, 1] und damit das gesamte „überabzählbar“. Also kann es also keine Bijektion zu N N geben. Beweis Seien x0, x1, x2, . Jedes [ [lässt sich im Zweiersystem eindeutig im Dualbruch mit { }der nicht in er-Periode endet, entwickeln. f:\mathbb {N}\rightarrow \mathbb {N} f : N → N. 2) Jede Obermenge einer überabzählbaren Menge ist überabzählbar. RE: Beweis dass R überabzählbar ist. Die Abbildung nach [0;1] folgt leicht aus der Ungleichung X1 k=n 0 2x k=3k 31 n 0; die fur alle (x k)

Ist die Potenzmenge der natürlichen Zahlen abzählbar?

2011, 20:30: leithian: Auf diesen Beitrag antworten » Hi, der klassische Beweis dass es keine . Soweit zum trivialen Fall.

abzählbar unendlich oder überabzählbar

deMan beweise (A∪B)\(A∩B)=(A\B)∪(B\A) | Matheloungemathelounge. Ich nehme an, dass es eine surjektive Menge g: N->C gibt.Die erste Menge die Überabzählbar ist ist eine Teilmenge von , . eine surjektive .

Zufallsexperiment: EIgenschaften der Ergebnismenge | Mathelounge

Die Menge der reellen Zahlen (R) überabzählbar unendlich

Der erste Beweis arbeitet mit anderen Eigenschaften der reellen Zahlen und kommt ganz ohne ein Zahlensystem aus. 2017Abzählbarkeit begründen10.

Überabzählbar unendlich

? Siehe Mengen im Wiki. Sei hierzu f : N → R beliebig.Beweis: Überabzählbarkeit.Neue Beweise für Existenz des mysteriösen „Planet 9“: „Spricht stark für seine Anwesenheit“. Setze D:= {a ∈ A: a! ∈ f {a)}.Definition (überabzählbar) Eine Menge A heißt überabzählbar, falls A nicht abzählbar ist.Hingegen ist die Menge R der reellen Zahlen überabzählbar unendlich. Meine Frage: Meine Frage ist es, wie ich es schaffe diese Aussage zu beweisen. Offenbar sind äquivalent: M ist überabzählbar. Bei einer überabzählbaren Menge M (oben) existieren für jede Funktion f : ℕ → M Elemente von M, die nicht im Bild von f liegen. Eine Menge M heißt.Die Menge der reellen Zahlen (R) überabzählbar unendlich – Beweis – YouTube. Beweis von Lemma 1: Die Aussage folgt mit Hilfe eines ähnlichen .Unter der Cantor-Menge, Cantormenge, auch cantorsches Diskontinuum, Cantor-Staub oder Wischmenge genannt, versteht man in der Mathematik eine bestimmte Teilmenge der Menge der reellen Zahlen mit besonderen topologischen, maßtheoretischen, geometrischen und mengentheoretischen Eigenschaften: Sie ist. ℤ ist abzählbar: 0, 1, −1, 2, −2, 3, −3, . Wie das ganze nun mit der Menge von ENDLICHEN Teilmengen . Als Hinweis wird angegeben das: Für jede Menge M die Potenzmenge M und die Menge Abb (M, {0,1}) für alle Funktionen: f: { M }\rightarrow \left\ { 0,1 .Also ist { } überabzählbar. Hier zählen wir alle gekürzten Brüche nach der Summe der Beträge von Zähler und .,|X|} eine totale Funktion, die jedem Zeichen x X die Stelle zuordnet, an der es im Alphabet. Wir definieren deshalb: Eine Menge M M heißt abzählbar unendlich, wenn sie zur Menge \dom N N der .

Bestimme ob endlich, unendlich abzählrbar oder unendlich überabzählbar? (mengen)? (Schule ...

Die Mächtigkeit einer abzählbar unendlichen Menge wird – als . Ich dachte an das 2. Satz brauchen wir. überabzählbar ist. Jetzt muss ich zeigen, dass die Cantor-Menge C überabzählbar ist.Wir wollen beweisen, dass die Menge der reellen Zahlen \(\mathbb{R}\) überabzählbar sind. Beim Nachweis der Abzählbarkeit arbeitet man aber meistens mit der oben .Ist [math]M[/math] eine Menge mit mindestens 2 Elementen, so ist [math]Abb(\mathbb{N},M)[/math] überabzählbar (Beweis wieder mit 2. non (|M| ≤ |ℕ|), d. Zeigen Sie mittels Diagonalisierung, dass die Menge P (N) überabzählbar ist.eine Abzählung von M. ii) Für jedes nichtleere offene Intervall (a, b) aus R ist die . 2017Beweis Abzählbarkeit10. 2017Abzählbarkeit beweisen10. Beweis: 1) Sei M eine abzählbare Menge und M‘ M eine unendliche Teilmenge. Doch gebe ich zu bedenken, dass mathematisch auch nicht alles bewiesen wurde und noch viel auf bloßen Überlegungen basiert, die es zu kritisieren evlt.

7 Endliche und abzählbare Mengen

Seien k 0, k 1, k 2, k 3, . Folgerung Die Menge ist überabzählbar. Aufgabe: Betrachten Sie die Cantor-Menge C und zeigen Sie, dass C überabzählbar ist.

Beweis: Überabzählbarkeit

Wenn ich das recht verstehe, wird eine Intervallschachtelung mit f(n) ∉ [an,bn] konstruiert. Wir notieren explizit: Korollar (Existenz transzendenter Zahlen) Es gibt überabzählbar viele transzendente Zahlen. Nicht abzählbare Mengen nennt man im Allgemeinen überabzählbar.Da dieser Beweis für jede Abbildung funktioniert, gibt es keine bijektive Abbildung zwischen der Menge der natürlichen Zahlen und der Menge der reellen Zahlen. Vergleich der Mächtigkeit einer Menge und ihrer .

R/Überabzählbar/Fakt/Beweis