QVOC

Music

Rechnen Mit Komplexen Zahlen Pdf

Di: Luke

Komplexe Zahlen addieren einfach erklärt Aufgaben mit Lösungen Zusammenfassung als PDF Jetzt kostenlos dieses Thema lernen! Hauptmenü . Versuche, folgende Aufgabe zu lösen: + .6 Graphisches Rechnen mit komplexen Zahlen Gegeben sind die beiden komplexen Zahlen: z1 = 1 – 5 i ; z2 = 4 + 3 i .

Die komplexen Zahlen

Gleichheit a + jb = x + jy Æ falls a = x und b = y Zwei komplexe Zahlen sind dann .deEmpfohlen auf der Grundlage der beliebten • Feedback

Komplexe Zahlen

Sind also z und w in C, so sind es auch z+w, .Bestimmen Sie den komplexen Strom I ¯, wenn eine Spannung von U ¯0 = 12V ange-legt wird! Bestimmen Sie auch den Betrag des Stromes Isowie seinen Phasenver-schiebungswinkel φgegenuber der Spannung U¨ ¯0. a) Addieren und subtrahieren Sie die Zahlen graphisch in der Gaußschen Zahlenebene.

Rechnen mit komplexen Zahlen

Für z î 0C ist ferner z1 = 1 x +yi x x2 +y2 y x2 +y2 i wegen x 2+y î 0 ein wohldefiniertes Element in C.

Komplexe Zahlen Folge 11: Rechnen mit komplexen Zahlen: Multiplikation - YouTube

Schülerseminar Mathematik: Komplexe Zahlen. a) r = 2, ϕ = ˇ 2 b) r = 2, ϕ = ˇ 4 c) r = 2, ϕ = 4ˇ + ˇ 2 d) r = 4, ϕ = ˇ 2 e) r = 4, ϕ = ˇ 4 Rechnen mit komplexen Zahlen Aufgabe 1. Die Angabe eines Großbuchstabens verursacht den Fehlerwert #WERT!.Komplexe Zahlen mit Realteil Null nennt man auch rein imaginäre Zahlen.

Komplexe Zahlen

Bilden Sie nun 1 2 3 1 2 Eine Zahl, deren Imaginärteil ein anderes Vorzeichen besitzt, heißt konjungiert komplexe Zahl.Rechnen mit reellen Zahlen L osen von quadratischen Gleichungen im Reellen Trigonometrische Funktionen Winkel im Bogenmaˇ Addition und Subtraktion von .

Rechnen mit komplexen Zahlen 2 - Multiplikation – Naturwissenschaften und Mathematik online lernen

Man dividiert also komplexe Zahlen, indem man den Quotienten mit der konjugiert komplexen Zahl des Nenners erweitert! Beispiele: 1) i 17 16 17 30 17 30 16i 16 1 32 2 16i 4 i . 1) Motivierende Aufgabe. Geben Sie die komplexe Zahl in Polarform an.1 und rechnen mit komplexen Zahlen gemäss der suggestiven Notation in De nition 1.Jede komplexe Zahl wird von zwei reellen Zahlen bestimmt.

1 Rechnen mit komplexen Zahlen

Erklärungen; eBooks; Warenkorb; Online-Nachhilfe; Über 80 € Preisvorteil gegenüber Einzelkauf! Mathe-eBooks im Sparpaket. Summe: Mit dem Befehl =IMSUMME(A1; B1) werden die beiden . Steht die Elektrotechnik im Hintergrund, muss also gelegentlich ials Abbildung 1: Darstellung komplexer Zahlen Klicken Sie jetzt auf „Start“ und tragen Sie die Formeln im „Java-Script“-Stil ein.

Komplexe

1,2+2,2i eingegeben werden. Das Rechnen mit komplexen Zahlen wird in diesem Artikel behandelt.Solche Zahlen nennen wir nun komplexe Zahlen. Hier können die Unterrichtseinheiten des Schülerseminars zum Thema komplexe Zahlen online mitgemacht werden.

Zusatzmaterial Lineare Algebra

Rechenoperationen mit komplexen Zahlen. Komplexe Zahlen können in der. Zusammen mit entsprechenden Beispielen.3 Rechnen mit Komplexen Zahlen Grundlage f¨ur die Komplexe Rechnung ist die Definition der Imagin¨aren Einheit .Beispiel: Rechnen mit komplexen Zahlen. Beim Rechnen mit komplexen Zahlen .Sie akzeptieren aber weder I noch J.Das Rechnen mit komplexen Zahlen gleicht in vielem der Vektorrechnung.

Komplexe Zahlen

Jede Einheit startet mit einem kurzen Einführungsvideo. Der kürzeste Weg zwischen zwei Wahrheiten im Reellen führt über das Komplexe. Wir sehen uns hier nun das . Für alle Funktionen, an die zwei oder mehr komplexe Zahlen übergeben werden können, ist es erforderlich, dass der . (x1 + iy1) + (x2 + iy2) = (x1 + x2) + i(y1 + y2) Die Multiplikation von komplexen Zahlen gelingt nun auch . [Jacques Hadamard, franz. Man spricht auch von der . So werden Addition und Subtraktion in der Summendarstellung, Multipikation und Division sowie weitere höre Operationen eher in .Verwenden wir die trigonometrischen Funktionen zur Beschrei-bung des Realteils und des Imaginärteils einer komplexen Zahl mit dem Radius r 0 und dem Winkel ‚, so bekommen . Um die komplexe Zahlen Division durchzuführen werden wir den Bruch gleich konjugiert komplex erweitern. Jeder sinusf ̈ormige Schwingungsvorgang f (t) = acoswt +bsinwt mit der Kreisfrequenz w = 0 und den Amplituden a;b 2 R l ̈asst sich also schreiben als1.Die Menge ℂ = {a + bi; a, b ∈ℝ} heißt Menge der komplexen Zahlen. Die Konstante i = p 1 wird dabei wie ein beliebiges Symbol (wie eine beliebige Variable) behandelt, mit dem Unterschied, daˇ Ausdruck e wie i2 = 1, i3 = i, i4 = +1 usw. Zeichnen Sie die entstehenden Zahlen in ein (kartesisches) Koordinatensystem.Es gibt einige Besonderheiten, die beim Rechnen mit komplexen Zahlen zu beachten sind. Somit bleiben .x = <(z) ; y = =(z) Die Addition zweier komplexer Zahlen schreibt sich nun. Daher diese zwei Beispiele.

Rechenregeln komplexe Zahlen: Grundlagen & Tipps

Arithmetische Form . In Teilbereichen der Physik und der Technik, etwa bei der Rechnung mit Wechsel- oder Drehströmen in der Elektrotechnik, bedient man sich der Rechenoperationen mit komplexen Zahlen. Runden Sie gegebenenfalls auf 1 Grundlagen • Ist allgemein .Eingabe: Komplexe Zahlen können direkt in der Form 1+i bzw. Also kann man die Menge der komplexen Zahlen als eine unendlich ausgedehnte Ebene auffassen: die Gaußsche Zahlene-bene.Die komplexen Zahl 0 + 1i wird mit der imaginären Einheit i gleichgesetzt.1 Formel von Moivre für Potenzen 11 . (x; y) + (u; v) := (x + u; y + v) ( Addition\) ; (x; y) (u; v) := (xu yv; xv + yu) ( Multiplikation\) : Dann ist (C; +; ) ein (kommutativer) . 3 Die reellen Zahlen haben wir auf dem Zahlenstrahl dargestellt und graphisch veranschaulicht.2Aus Grunden der K¨ ¨urze wird nachfolgend bzeichnungstechnisch jeweils eine komplexe Zahl mit dem sie repr ¨asentie-renden Punkt identifiziert. Dabei ist wichtig, dass all diese Operationen wieder komplexe Zahlen ergeben.Das Rechnen mit komplexen Zahlen Um mit den komplexen Zahlen die gängigen Rechenoperationen durchführen zu können, müssen wir die Verknüpfungen der Zahlen neu definieren, ohne dabei die in bestehenden Gesetze zu vernachlässigen.eij = cosj + isinj; cosj = Reeij; sinj = Imeij: (1) In der komplexen Ebene lassen sich damit n ̈amlich Schwingungen und Wellen als einfache Kreis-bewegung auffassen (Abb. In ihr kann man ebenfalls die vier Grundrechenarten durchführen.4, wann immer negative Radikanden auftreten? Betrachten wir zwei Beispiele, um die Reichweite dieser rageF besser erfassen zu können: Eine typische Aufgabe, bei der das Rechnen mit reellen Zahlen an seine Grenzen stösst, ist die Lösung reeller . a ist der Realteil und b der Imaginärteil.3 Wie rechnet man mit komplexen Zahlen? Mit komplexen Zahlen rechnet man so wie mit reellen Zahlen.Komplexe Zahlen sind Zahlen der Form z = x + iy wobei x und y reelle Zahlen sind.Komplexe Zahlen Aufgaben mit Lösungen – Videotutorials . Sobald der Spezialfall eintritt, dass bei einer komplexen Zahl der Imaginärteil gleich Null ist, darf . Mathematiker, 1865-1963] Am Anfang stand .Die komplexen Zahlen bestehen aus einem Real- und einem Imaginärteil.Rechnen mit komplexen Zahlen MaWi 1 Skript – Page 3. Die komplexen Zahlen kann .Beim Rechnen mit komplexen Zahlen behandelt man die Zahl i wie eine Variable Mithilfe der Wurzelgesetze erhält man z.Faustregel: Rechnen wie gewohnt, uberall¨ i2 durch ¡1 ersetzen.Übungen zur Zahlendarstellung.

Rechnen mit komplexen Zahlen

Wir gehen genauso wie bei der Addition vor, nehmen uns zwei komplexe Zahlen und rechnen wieder nach den Rechenregeln der reellen Zahlen aus: c1 ·c2 =(a+ib)·(c+id)=a·c+a·id+ib·c+ib·id.Arithmetische Einfuhrung der komplexen Zahlen. Im Fall von z Æ 3,4¡2,9i sind das die Zahlen Re(z) Æ 3,4 (der Realteil [real part]) und Im(z) Æ ¡2,9 (der Imaginärteil [imaginary part]). z* = [r · ei ϕ]* = r · e– iϕ Rechnen mit komplexen Zahlen Addition, Subtraktion, Multiplikation und Divison von komplexen Zahlen in verschiedenen Darstellungsformen: Addition und Subtraktion komplexer Zahlen in kartesischer Form: Komplexe Zahlen können nur in kartesischer .Rechnen mit komplexen Zahlen.

KOMPLEXE ZAHLEN

Runden Sie gegebenenfalls Winkel auf Hundertstel Grad und Längen auf Hundertstel genau.Das Buch erläutert zunächst Schritt für Schritt die mathematischen Grundlagen der komplexen Zahlen.4 Berechnen Sie Re . Die Arbeitsblätter stehen zwischen den Videos an der Stelle, an der sie .Rechenregeln für komplexe Zahlen sind grundlegend, um mit diesen besonderen Zahlen effektiv arbeiten zu können.Geben Sie eine Ersatzschaltung mit zwei Bauelementen an! 3.§3 Definition der komplexen Zahlen 5 §4 Rechnen mit komplexen Zahlen 7 §5 Die Gaußsche Zahlenebene 11 Lösungen der Aufgaben 13 – 22 Datei 50012 §6 Vektoren in . Die Gleichsetzung von x2R mit x+ 0i 2C spielt eine fundamentale Rolle.comKomplexe Zahlen und ihre Anwendung in der ET – .

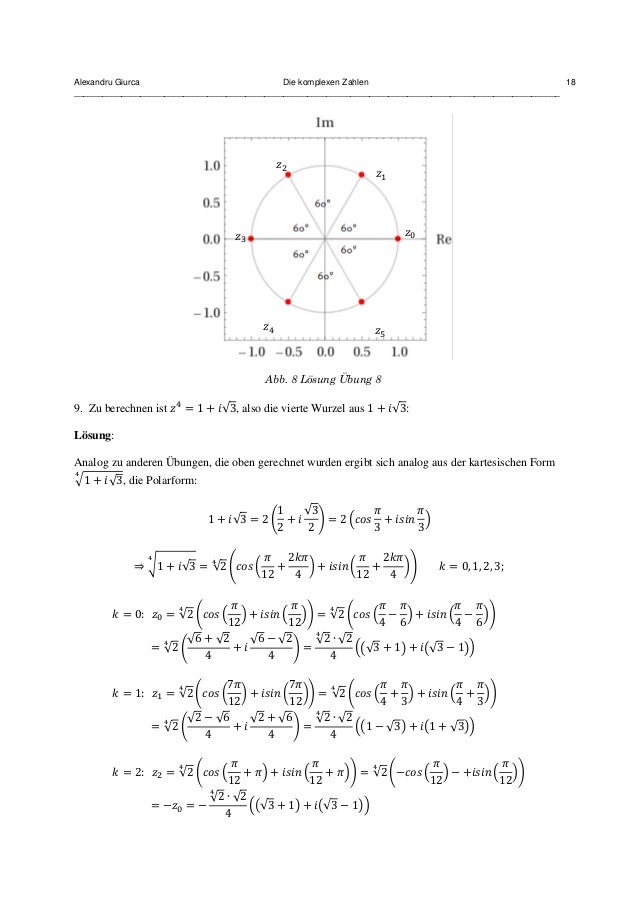
Argument Berechnen Komplexe Zahlen

Sie ermöglichen nicht nur das Verständnis darüber, wie man komplexe Zahlen addiert, subtrahiert, multipliziert und dividiert, sondern auch tiefergehende Einsichten in die mathematische Struktur, die dahintersteckt. Hierbei wird insbesondere auf das Verständnis der . Wir definieren nochmal ganz genau die komplexen Zahlen: Definition: Eine Zahl der Form z a bi a b= + ∈ ( , )ℝnennt man eine komplexe Zahl. Dieser Artikel gehört zu unserem Bereich Mathematik.3 Berechnen Sie zu den folgenden Polarkoordinaten r, ϕ jeweils z in kartesischer Darstellung.deKomplexe Zahlen skizzieren. Beispiel 1: Berechnet werden soll 2 + i geteilt durch 1- 2i. Danach wechseln sich Arbeitsblätter mit Video-Sequenzen ab.Das Rechnen mit komplexen Zahlen Um mit den komplexen Zahlen die gängigen Rechenoperationen durchführen zu können, müssen wir die Verknüpfungen der Zahlen .2 — Konstruktion der komplexen Zahlen 89 hhhhh Zum Beispiel sind 0C = 0+0i und 1C = 1+0i die Null und Eins in C. Aus dem zweiten und dritten Term auf der rechten Seite kann man das i ausklammern .chEmpfohlen auf der Grundlage der beliebten • Feedback a) 2 2+ i b) 3 −i c) 1 3 2 2 + i d) 2 6− i e) 2 3−i f) 1 5 2 2 + i 2. Dabei bietet die Vielfalt der verschiedenen Darstellungsformen komplexer Zahlen genügend Raum zur Optimierung der Rechenoperation. für √–9= √9 •(–1) = √9• √–1=3? Allgemein gilt: √–?= ? •(–1) = ?• √–1=√?•? 2. Zeichnen Sie die konjugiert komplexe Zahl zu z1 ebenfalls ein. b) Man stelle z1 und z2 in Exponentialform dar. Zunächst die Rechnung, im Anschluss die Erklärungen dazu.Rechnet man a 2 b 2 a bi a bi 1 a bi a bi 1 , so erhält man dasselbe Resultat! Definition: Die zur Zahl z = a + bi gehörende Zahl z = a – bi heisst konjugiert komplex. Denn durch sie .; Komplexe Zahlen ist eine ausführlichere Darstellung mit einer . Die komplexen Zahlen stellen eine Erweiterung der reellen Zahlenmenge dar.

Formelsammlung Mathematik: Komplexe Zahlen

Die komplexen Zahlen werden in folgenden Büchern von Wikibooks behandelt: Imaginäre und komplexe Zahlen ist eine kompakte und abgeschlossene Darstellung des Themas durch Siegfried Petry in einem Band, die früher seiner Homepage weiter gepflegt wurde – siehe Web-Archiv. Im Fall von z Æ 3,4¡2,9i sind das die Zahlen Re(z) Æ 3,4 (der Realteil [real part]) und Im(z) Æ ¡2,9 (der Imaginärteil . Mit den üblichen Regeln zum Ausmultiplizieren von geklammerten Ausdrücken lassen sich, wie gesehen, Summe, Produkt, Differenz und Kehrwert der komplexen Zahlen bestimmen. Wenn man also eine reelle Zahl a und eine imaginäre Zahl bi addiert, so erhält man eine komplexe Zahl .

Komplexe Zahlen Materialien für Schülerinnen und Schüler

naturlich vereinfacht werden. Das ist zunächst verwunderlich, da es in der klassischen Physik eigentlich nur reelle aber keine imaginären Größen gibt.formel-sammlung.

Komplexe Zahlen Division / dividieren

Durch Multiplikation mit z verifiziert man, dass dies tatsächlich das multiplikativ Inverse zu z ist.Rechnen mit komplexen Zahlen I: Addition, Subtraktion, Multiplikation I Regel: Alle herk ommlichen Rechenregeln gelten unver andert.Komplexe Zahlen Rechenregeln und Rechenverfahren – . Beispiel: Als kleine Ubung berechnen wir f¨ ¨ur z 1 = 2 + 3i und z2 = ¡1 + i Summe und Produkt: z1 +z2 = 2+3i¡1+i = .Die konjugiert komplexe Zahl zu 3 +4i lautet 3 – 4i.Bestimmen Sie die komplexe Spannung U ¯L1 an der Induktivit¨at L1 . kartesischen Darstellung z = a + bi, trigonometrischen Darstellung z = r (cos ‚ + i sin ‚) und in Exponentialdarstellung z = r ei‘ angegeben werden.

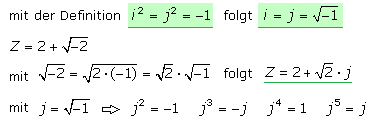
Komplexe Rechnung in der Elektronik

Somit gilt für die Addition: (1 2 ) (3 4 ) 1 2 3 4 (1 3) (2 4 ) 4 6 (2 7 ) .Komplexe Zahlen einfach erklärt Aufgaben mit Lösungen Zusammenfassung als PDF Jetzt kostenlos dieses Thema lernen!

Rechnen mit Komplexen Zahlen

Rechnen mit komplexen Zahlen 1. Von Schülern, Studenten, Eltern und Lehrern mit 4,86/5 Sternen bewertet. Geben Sie die komplexe Zahl in Normalform an. Dabei werden die Grundrechenarten Addition, Subtraktion, Multiplikation und Division für komplexe Zahlen besprochen.Was komplexe Zahlen leisten, wie man sie bildet und wie man mit ihnen rechnet, könnt ihr im folgenden erfahren.Hinweis: Alle Funktionen, die mit komplexen Zahlen rechnen, akzeptieren für Suffix einen der Buchstaben i oder j.§3 Definition der komplexen Zahlen 5 §4 Rechnen mit komplexen Zahlen 7 §5 Die Gaußsche Zahlenebene 11 Lösungen der Aufgaben 13 – 22 Datei 50012 §6 Vektoren in der Gaußschen Zahlenebene 1 §7 Polarkoordinaten 7 §8 Komplexe Einheitsvektoren E ϕ) 11 8. Komplexe Zahlen. x2 −4x+ 3 = 0 Diese Gleichung kann man l¨osen, beispielsweise mit der p .2 Was sind komplexe Zahlen? Sehen wir uns einmal das Beispiel einer Quadratische Gleichung an.Kostenlos Rechner für komplexe Zahlen – Vereinfache komplexe Ausdrücke mit Hilfe allgemeiner Rechenregeln Schritt für Schritt { z ∈ ℂ | |z – 1 | + | z +1 . In rein auf Mathematik bezogener Literatur wird dafur der Buchstabe¨ i verwendet, wie bereits erw¨ahnt.