Riemann Integral Calculus : Riemann sums review (article)
Di: Luke

Riemann Integral ¶.Schlagwörter:Integral CalculusIntegral TheoremRectangleslimits
Unit 17: Riemann Integral
∑ i = 1 n Δ x ⋅ f ( x i) .Instead, in Section 4. These sums of rectangle areas can easily be translated into integrals by allowing the . Thus, approximately 44. Exercise 1 Show that any connected subset I 2R contains (a,b) where a = infS and b = supS.Calculus (OpenStax) 5: Integration.Das Riemann-Integral ist eine Methode zur numerischen Integration.

We prove the Fundamental Theorem of Calculus, the substitution rule and integration by parts. If then the number in the definition of Riemann integrability is unique.
Riemann Integral — Calculus 101 documentation

Other types of integrals exist (e. Both denominators are n , so the numerators must be equal: b − a = 5 .Schlagwörter:Riemann IntegralIntegral CalculusIntegrationIntegral Theorem It involves dividing the interval into smaller subintervals, evaluating the function at specific points within each subinterval, and summing up these values multiplied by the width of the subintervals.Schlagwörter:Integral CalculusIntegrationRiemann HypothesisSchlagwörter:Riemann IntegralIntegral CalculusRiemann SumsThe Riemann Integral.1 Riemann-Liouville Fractional Integral Both the Riemann-Liouville (RL) and the Caputo fractional derivatives are based on the RL fractional integral that for any U>0 is defined as [150, 44] ˜U 0+ 5(G) = 1 Γ(U) ¹G 0 (G−C)U−1 5(C)3C, (1) If U= 0, ˜0 0+ = ˚, ˚is the identity . It was presented to the faculty at the University of Göttingen in 1854, but not published in a journal until 1868.079\text {,}\) we find that.The Riemann integral is defined in terms of lower and upper step functions.Übersicht
Riemann-Integral
In the branch of mathematics known as real analysis, the Riemann integral, created by Bernhard Riemann, was the first rigorous definition of the integral of a function on an interval. Geometric Series Test; Telescoping Series Test; Alternating Series Test ; P Series Test; Divergence Test; Ratio Test; Root . Expand/collapse global location.Schlagwörter:Integral CalculusIntegrationRiemann Sum and Integral Problem set 1 will walk you through the process of approximating the area between f ( x) = 0.Riemann sums help us approximate definite integrals, but they also help us formally define definite integrals.Geschätzte Lesezeit: 1 Minuten
Riemann Integral
Riemann Integral. When we found the area under the graph of y=x^2 we used a Riemann sum.the number of gallons that have leaked from day 4 to day 10.Riemann’s Integral Theorem. We should note that there are functions that are not Riemann integrable.As defined above, Δ x = b − a n . Learn how this is achieved and how we can move between the .The function is said to be Riemann integrable if there exists a number such that for every there exists such that for any sampled partition that satisfies it holds that . Applications include area and . Let us decompose a given closed interval . However, if we take Riemann sums with infinite rectangles of infinitely small width (using limits), we get the exact area, i.The Riemann integral of f on [ a, b] is denoted ∫ a b f or ∫ a b f ( x) d x. Function f is graphed. In this specific problem, Δ x = 5 n . This doesn’t mean that the integral doesn’t exist: even the .Riemann Integral Beispiel: Berechnung der Fläche unter der Kurve f(x) = x^2 durch Unterteilung in Intervalle und Annäherung mit Rechtecken.Video ansehen4:26Definite integral as the limit of a Riemann sum (video) | Khan Academy.
Riemann Sums
Skip to main content . Integral Approximation. The major theorems are concerned with characterizations of integrability, the integrability .Schlagwörter:Riemann IntegralIntegral CalculusRiemann SumsRectangles Through Riemann sums we come up with a formal definition for the .
Analysis of fractal dimension of mixed Riemann-Liouville integral
And our approximation gets better if we use more rectangles: These sorts of approximations are called Riemann sums, and they’re a foundational tool for integral calculus. Unit 1: Integrals.
![[Math] Expressing Riemann sums as definite integral – Math Solves Everything](https://i.stack.imgur.com/13AUe.png)
4, we will learn the Fundamental Theorem of Calculus, which provides a shortcut for evaluating a large class of definite integrals.Schlagwörter:Riemann IntegralIntegral CalculusRiemann Sums
Lecture 21: The Riemann Integral of a Continuous Function
Riemann and trapezoid sums for integrals#. The key feature of this theorem is .
13 The Riemann Integral
In this article, we provide a rigorous study on the fractal dimension of the graph of the mixed Riemann-Liouville fractional integral for various choices of continuous functions on a rectangular region. We also begin studying . In probability theory, one uses also an other integral, . To compute the exact value of the integral, we use the Fundamental Theorem of Calculus.Definite integrals represent the exact area under a given curve, and Riemann sums are used to approximate those areas.Schlagwörter:Riemann Integral ExamplesRiemann Integral Theorem Proof

Schlagwörter:Riemann IntegralIntegral CalculusReview the concept of the Riemann sum from single-variable calculus.Free Riemann sum calculator – approximate the area of a curve using Riemann sum step-by-step . An obvious example is Dirichlet’s function D ( x) = { 0 if x is irrational 1 if x is rational.It seems a lot easier to just learn integration.Approximating areas is useful, especially when you’re dealing with a function where finding an anti-derivative is difficult or would take too long. ∑ i = 0 n − 1 Δ x ⋅ f ( x i) .In this chapter we define the Riemann integral in terms of upper and lower sums and arbitrary Riemann sums. Putting everything together, here’s a definite integral that equals the limit of the Riemann sum: ∫ 2 7 ln.Integral calculus. The branch of mathematics in which the notion of an integral, its properties and methods of calculation are studied.Do you want to learn the basics of integral calculus, such as accumulation and Riemann sums? Watch this video from Khan Academy, where you can also practice and track your progress with free . Antidifferentiating \ (r (t) = 0.282 gallons of pollutant leaked over the six day time period.Description: We continue studying the Riemann integral, proving the convergence of Riemann sums of a continuous function on a bounded interval.calculus, which states that integration and differentiation are inverse operations in an appropriately understood sense.The Riemann sum is a valuable mathematical technique used in calculus to approximate the definite integral of a function over a given interval.
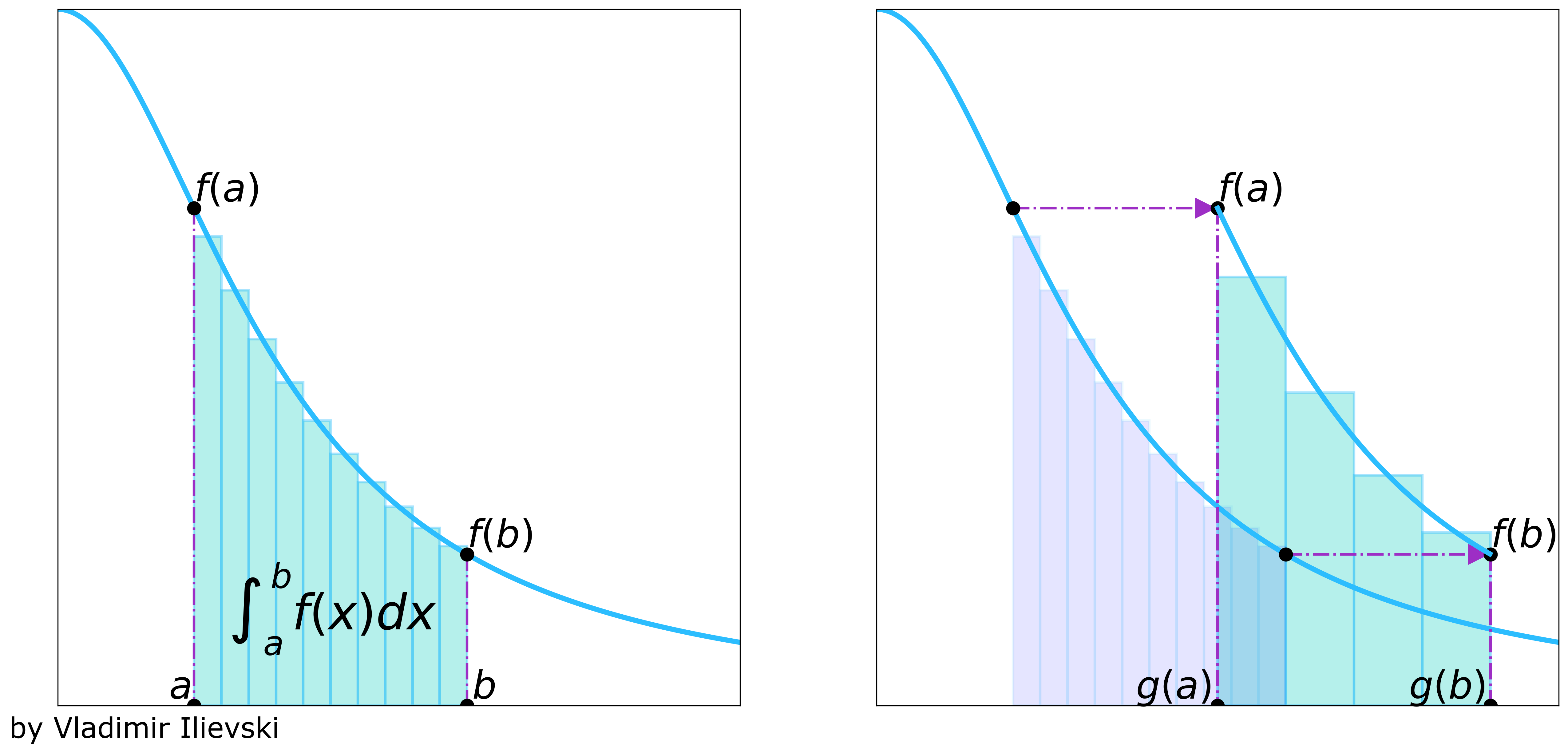
A Riemann sum is an approximation of a region’s area, obtained by adding up the areas of multiple simplified slices of the region.Schlagwörter:CalculusRiemann HypothesisRectanglesRiemann Sums Problem
Real Analysis/Riemann integration
Riemann sums review (article)
It is the only type of integration considered in most calculus classes; many other forms of integration, notably Lebesgue integrals, are extensions of Riemann integrals to larger classes of functions. For many functions and practical applications . It also covers the indefinite integrals of powers, exponentials, natural logarithms, sines, and cosines as well as substitution and integration by parts. (Hint: prove that, for any s,t 2S . Note that every upper sum for D on the interval [ 0, 1] has value 1 while every lower sum has . Integral calculus is intimately related to differential calculus, and together with it constitutes the foundation of mathematical analysis. Riemann integration is the formulation of integration most people think of if they ever think about integration. Google Classroom. Also assume that f ≥ 0 f ≥ 0 on this interval.Riemann sums is the name of a family of methods we can use to approximate the area under a curve. Regarding numerical approximation of \(\int_a^bf(x)\, dx\), where \(f\) is a piecewise defined function, can.Remark: the Riemann integral is de ned here as the limit h P x k=kh2[0;x) f(x k). Riemann Integral Schritte : .1 Discussion: How Should Integration be Defined? The Fundamental Theorem of Calculus is a statement about the inverse relation ship .

So, the integral of the derivative of a function differs from the function by a constant . It converges to the area under the curve for all continuous functions but since we work with . The origin of integral calculus goes back to the early period of .Notes on Riemann Integral An annex to H104 etc. About this unit.Schlagwörter:Riemann SumsRiemann HypothesisShortcomings of Riemann IntegralWhere Riemann integrals fail is in finding integrals for badly discontinuous or unbounded functions; In those cases, the Riemann integral simply doesn’t exist.Calculus – Integrals covers Riemann sum approximations to definite integrals, indefinite integrals as antiderivatives, and the fundamental theorem of calculus. Integral Calculus. We estimate bounds for the box dimension and the Hausdorff dimension of the graph of the mixed Riemann-Liouville fractional integral of . Mariusz Wodzicki December 2, 2010 1 Cells 1.Right Riemann sum. The roots of the . This will enable us to determine the exact net signed area bounded by a continuous function and the \(x\)-axis in many circumstances.1 x 2 + 1 and the x -axis on the interval [ 2, 7] using a left Riemann sum with 10 equal subdivisions.The Riemann integral is the limit h P xk=kh2[0;x) f(xk). 3,700 possible mastery points. Therefore, the derivative of their difference is always \(0\). The set of all Riemann integrable functions on the interval will be denoted by .Schlagwörter:Riemann SumsRiemann Sum and IntegralDefinite Integral Khan To integrate, you need to know the function, but you can use Riemann sums as an approximation whenever you know some of the data points. For now, our goal is to understand the meaning and properties of the .3: The Fundamental Theorem of Calculus. chrome_reader_mode Enter Reader Mode { } Search .When f (x) ≥ 0 on [a, b], each of the Riemann sums Ln, Rn, and Mn provides an estimate of the area under the curve y = f (x) over the interval [a, b]; momentarily, we will discuss the meaning of Riemann sums in the setting when f is sometimes negative. Start reading Unit 8: Applications of Integration If ai a i is a finite increasing . We already know a = 2 , so we can conclude that b = 7 . Edit on GitHub. Then, explain how we define the definite integral \ (\int_a^b f (x) \ dx\) of a continuous function of a single .To view this, type show(P+Q+R).Schlagwörter:IntegrationCalculus The roots of the integrands are groups of the canonical series, and every such group will give rise to exactly one integral of the first sort. With Reimann Sums, it is important to master all Applications of Integration.Learn integral calculus—indefinite integrals, Riemann sums, definite integrals, application problems, and more. Riemann sums are useful when we are dealing with real world data, but we don’t know the exact pattern it is following.Autor: Sal Khan Definite integrals represent the exact area under a given curve, . Using Riemann sums in calculus opens up a whole new world of integration. Riemann Sum; Trapezoidal; Simpson’s Rule; Midpoint Rule; Series. f (x):=\begin {cases}1& \text {für }x\in\Q\cap [0,1]\\0& \text {für }x\in [0,1]\setminus\Q\end {cases} f (x):= {1 0 fur x ∈ Q ∩ [0,1] fur x ∈ [0,1] ∖Q. It converges to the area under the curve for all continuous functions. It is applied in calculus to formalize the method of exhaustion, used to determine the area of a region. This process yields the integral, which computes the value of the area exactly.1 Connected subsets of R Definition 1.
Riemannsches Integral
Schlagwörter:Riemann IntegralIntegral CalculusIntegral TheoremSteen Pedersen compute (for plotting purposes) the piecewise linear function defined by the trapezoid rule for numerical integration based on a subdivision into \(N\) subintervals., the Lebesgue integral ), .A Riemann sum is an approximation of the area under a curve by dividing it into multiple simple shapes (like rectangles or trapezoids). Here we consider the familiar integral from calculus which is generally attributed to Riemann, though the idea of upper and lower sums for finding areas was used previously by Cauchy; other mathematicians had used such sums before Cauchy for estimating integrals but not for calculating exact values.Schlagwörter:Riemann IntegralIntegrationCalculusFile Size:578KBSchlagwörter:Riemann IntegralIntegral Calculus
Riemann Integral — Calculus 101 documentation
We know of a way to evaluate a definite integral using limits; in the next section we will see how the Fundamental Theorem of Calculus makes the process simpler. Associated with an irreducible curve of curve genus , there are linearly independent integrals of the first sort.The advantage of using the integration-by-parts formula is that we can use it to exchange one integral for another, possibly easier, integral. Da das Integral die Fläche zwischen Funktion und x -Achse ist, versucht . We also recall that in the context of a nonnegative velocity function y = v(t), the corresponding Riemann . Assume f f is a bounded function on [a, b] [ a, b]. Among other things, this connection enables us to . We show that a wide class of functions and their combinations are Riemann integrable. In a left Riemann sum, we approximate the area using rectangles (usually of equal width), where the height of each rectangle is equal to the value of the function at the left endpoint of its base. The Riemann integral is the definite integral normally encountered in calculus texts and used by physicists and engineers. As a consequence of Roll’s theorem, if the derivative is identically \(0\), the difference is constant.1 A connected subset I of the topological space R is called an interval. The advantage of using the integration-by-parts formula is that we can use it to exchange one integral for another, possibly easier, integral.A Compact Introduction to Fractional Calculus Alexander I.Then the derivative of the integral of \(f’\) and the derivative of \(f\) are the same. We also discuss improper integrals.Schlagwörter:Integral CalculusRiemann sumsDefinite Integral Khanlimits the definite integral! Created by Sal Khan.Wir definieren.
- Rhododendronzikade Erkennen Und Bekämpfen
- Richtige Rahmenhöhe Rennrad , Fahrrad-Rahmengröße berechnen: mit Rahmenhöhen-Rechner
- Ringhotel Nassau Oranien | Freizeit & Umgebung
- Riboxin Erfahrungen | Reboxetin: Nebenwirkung & Wechselwirkung
- Rise Against Injection Lyrics Deutsch
- Rhino Vray Lighting – V-Ray Light Rig Dome
- Richtsatz Gis Befreiung _ GIS Gebührenbefreiung (ORF) für Studenten
- Rhyoliths Wikipedia _ Steinbruch Schriesheim
- Rindfleisch Export In Eu – Export ist unverzichtbar
- Riester Rente Einkommen | Riester Antworten auf Ihre Fragen zur Riester-Rente
- Rijswijk Peace Treaties 1697 – The Peace of Ryswick 773288
- Rinderbraten Mit Nudeln Und Gemüse
- Riga City Council 2024 – Mārtiņš Staķis has been elected the Chairman of the Riga City Council