QVOC

Music

Rotation Matrix In 3D , Derivation of basic rotation matrices in three dimensions

Di: Luke

Eine aufwändige Berechnung der Inversen entfällt jedoch, weil die Inverse einer Drehmatrix ihrer Transponieren entspricht: D − 1 = D T. What you proposed, though -rotating around an extra axis-, is also done. specify: – axis of rotation (2 d. At issue is whether you can write code that is intuitive to read and works the first time, or whether it requires a lot of work to decipher, or a . ROMANIA_engineer. Zur Erinnerung: Transponieren heißt, die Einträge der Matrix an ihrer Hauptdiagonalen zu spiegeln . Find more Mathematics .)

Derivation of basic rotation matrices in three dimensions

Input angle format Radians Degrees.A rotation’s matrix has determinant 1, while a reflection’s matrix has determinant -1.This notebook demonstrates how to use clifford to implement rotations in three dimensions using euler angles, rotation matices and quaternions. You can multiply the expression for z by 3, z = 3*z.R(ˆn, π) = R(−ˆn, π) , (6)

Drehmatrix • Rotationsmatrix, Vektor drehen · [mit Video]

This corresponds to the following quaternion (in scalar-last format): >>> r = R.Euler angels are useful for describing 3D rotations in a way that is understandable to humans, and are therefore commonly seen in user interfaces. 3D rotation, Euler angles • A sequence of 3 elemental rotations • 12 possible sequences – .Transforms in 3D. Let v =n1 ×n2/∥n1 ×n2∥; that’s one of the two unit vectors in the intersection P1 ×P2. All of these forms are derived from the more general rotor form, which is provided by GA.Based on Daniel F’s correction, here is a function that does what you want: import numpy as np def rotation_matrix_from_vectors(vec1, vec2): Find the rotation matrix that aligns vec1 to vec2 :param vec1: A 3d source vector :param vec2: A 3d destination vector :return mat: A transform matrix (3×3) which when applied to vec1, .Yet another way of specifying the rotation matrix is through a rotation axis vector, \({\bf p}\), and a rotation angle, \(\alpha\), about the \({\bf p}\) axis., yaw-pitch-roll) –Angle-axis (Euler axis and angle): nonlinear optimization, robotics –Quaternion: many compositions of rotations (e. asked Jan 16, 2013 at 20:34. When acting on a matrix, each column of the matrix represents a different vector. The final matrix you want is CBA (in that order, assuming right-multiplication with vectors) answered Aug 5, 2016 at 9:04. This vector space has a scalar product, which defines lengths of vectors and angles between them, as usual. Grundsätzlich gelten für 3D-Operationen die gleichen Betrachtungen wie für 2D. Now we can describe a step by step . But practically speaking, in our opinion, it is quite important.

Deriving the 3D Rotation Matrix

Rotation in 2D.Vector(4,5,6)print(r * v)See more on stackoverflowFeedbackVielen Dank!Geben Sie weitere Informationen anPython list rotation – Stack Overflowmath – Rotate point about another point in degrees python . Unfortunately, converting back and forth between Euler angles .In linear algebra, a rotation matrix is a transformation matrix that is used to perform a rotation in Euclidean space. R = rotx(ang) creates a 3-by-3 matrix for rotating a 3-by-1 vector or 3-by-N matrix of vectors around the x-axis by ang degrees.A rotation is a trans-formation with the property that the vector consumed by the machine and the vector spit out by the machine have the same length.

Rotation formalisms in three dimensions

That’s not so hard to construct, surprisingly. ? Related Topics:Matrix Multiplication. Conversion from the rotor form to a matrix representation is shown, and takes about three lines of code. The trace of the rotation is made using multiple vectors at 5° increments. Scale the surface by the factor 3 along the z-axis.3D rotation •Formalisms and example uses –Euler angles: platform or gimbal orientation (e. Rotation matrix. 2) Rotation about the y-axis: . Thus, the decision is entirely a cosmetic one.5k 30 30 gold badges 205 205 silver badges 202 202 bronze badges. We assume this vector space includes an orthonormal basis . A rotational operation on the 3D array can be completed by inserting the rotation matrix into .When he rotates in the Y and Z dimensions, the rotation goes around the X axis.

3D Rotations: Intuitions And Limitations

Our goal is to . For the rotation matrix R and vector v, the rotated vector is given by R*v. In this case, the rotation matrix is written as \[ {\bf R} = \cos \alpha \; {\bf .3D Rotations are used everywhere in Computer Graphics, Computer Vision, Geometric Modeling and Processing, as well as in many other related areas.comEmpfohlen auf der Grundlage der beliebten • Feedback

Three-Dimensional Rotation Matrices

Rotation matrix in 3D space.random_rotmat(size=(), dtype=torch.

Rotation matrix

comlinear algebra – Finding the rotation matrix in n-dimensions . Then R_theta=[costheta -sintheta; sintheta costheta], (1) so v^’=R_thetav_0.det(R) = 1 d e t ( R) = 1. Use for example tuple() to generate a single element, and (5,2) to generate a 5×2 batch. So sehen die dritte Zeile und die dritte Spalte wie ein Teil der Identitätsmatrix aus, während der obere rechte Teil wie die 2D-Rotationsmatrix aussieht. Since R(nˆ,θ) describes a rotation by an angle θ about an axis nˆ, the formula for Rij that we seek When he rotates in the Z and X dimensions, the rotation goes around the Y axis.comRotation Matrix – an overview | ScienceDirect Topicssciencedirect. • Transforms a cube into a general parallelepiped. Auch hier ist die Anwendung der homogenen Koordinaten angebracht, da auch hier die . If you want to rotate a vector you should construct what is known as a rotation matrix. These matrices are represented as 2D NumPy arrays.from_quat([0, 0, np. The case N = 2 N = 2 is a simple exercise in which you can find a parametrization in terms of cosine and sine for a general rotation matrix in two .• Common 3D rotation formalisms – Rotation matrix • 3×3 matrix (9 parameters), with 3 degrees of freedom – Euler angles • 3 parameters – Euler axis and angle • 4 parameters, axis vector (to scale) – Quaternions • 4 parameters (to scale) CSE 167, Winter 2018 11 .

Lecture 02b: Rotation Matrices - 3D Rotations

• Change in each coordinate is a linear combination of.

Geometric transformations in 3D and coordinate frames

3D Rotation in Computer Graphics ~xRay Pixy - YouTube

Computer Graphics

Vector arguments are what numpy refers to as array_like and can be a list, tuple, numpy array, numpy row vector or numpy .Rotation matrices describe the rotation of an object or a vector in a fixed coordinate system.Plenty more on Google. Applying multiple general .Scale and Rotate.

Rotation Matrices

• To generate a rotation in 3D we have to. The vector space Operations and coordinates. This is no longer a matrix rotation, but a quaternion rotation. For example, using the convention below, the matrix. = Rv , where kwk = kvk.obtain the general expression for the three dimensional rotation matrix R(ˆn,θ).When discussing a rotation, there are two possible conventions: rotation of the axes, and rotation of the object relative to fixed axes.

Rotation matrix in 2D and 3D

So v,n2,w is an orthonormal basis for 3-space. Mar 4, 2018 at 22:09 @YngveMoe I would say it does work: you need to use the coordinate vector for each of the raster points and calculate its new positions by multiplying it with .Using a matrix to encode this operation. These matrices are widely used to perform computations in physics, geometry, . NewGradDev NewGradDev.3d matrix rotation. See also complex .Visualizing 2D/3D/4D transformation matrices with determinants and eigen pairs.The Mathematics of the 3D Rotation Matrix – Fastgraphfastgraph. We consider a vector space, either a 2D or 3D one.comEmpfohlen auf der Grundlage der beliebten • Feedback

Rotation Matrix

x y z w (real part) Axis-angle.A rotation transformation matrix is used to calculate the new position coordinate P’, which shown as below: Rotation along x-axis. But since we’re rotating around a fixed axis, it behaves exactly like the 2D case with one of the dimensions ignored.

Curso 3D Math: 15 - Rotation Matrix - YouTube

pi/4)]) The rotation can be expressed in any of the other formats:

rotation

import math3d as m3dr = m3d. Matrix: Visualizing 2D/3D/4D transformation matrices with determinants and eigen pairs. Parameters: size ( tuple or int) – batch size. As a matrix equation, if R is a rotation matrix and v is a vector, then.Rotation matrix Derivation of rotation matrix for 2D and 3D, from scratch. Viewed 4k times.Video ansehen5:05? In this video we derive the Rotation Matrix that represents a coordinate transformation by rotation over an angle.The points form a vector that can be rotated about the , , or axes., yaw-pitch-roll) –Angle-axis (Euler axis and angle): nonlinear optimization, robotics . Let u =v ×n1; that’s a unit vector in the first plane, perp.) – amount of rotation (1 d.Rotation matrix. Axis x y z Angle (radians) Axis with angle magnitude . Get the free Rotation Matrix in 3D widget for your website, blog, Wordpress, Blogger, or iGoogle. The more general approach is to create a scaling matrix, and then multiply the scaling matrix by the vector of coordinates. Consider a counter-clockwise rotation of 90 degrees about the z-axis.Because rotation matrices are orthogonal, their inverse is the same as their transpose (see Section 6. The first one imply the rigidity of the rotation ( v ⋅w =vRT ⋅ Rw v ⋅ w = v R T ⋅ R w ), while the second one select rotations without reflection about an axis. Follow edited May 30, 2016 at 8:50.The underlying object is independent of the representation used for initialization. Matrix: show eigenvectors show bounding cube cull “infinity” lines due . B: your rotation (Euler angles or whatever) C: translation by plus P. Rotation matrices, on the other hand, are the representation of choice when it comes to implementing efficient rotations in software.Rotations About The Same Axis In 3D Are Also Commutative — In general, the composition of 3D rotations is not commutative. In R^2, consider the matrix that rotates a given vector v_0 by a counterclockwise angle theta in a fixed coordinate system. There are many different, and apparently unrelated, ways of .

Better rotation representations for accurate pose estimation

I’ve been reading up on rotation transformation and following this .The rotation matrix along the arbitrary axis in 3D space is given by Rodrigous’ rotation formula . Each of these vectors is the product of a rotation matrix .new_axis_angle([1,2,3], 1)v = m3d.

3D Rotation in Computer Graphics - Tutorial And Example

3D rotation is very similar except that of course we need an extra dimension.Zum Beispiel führt die Yaw-Matrix im Wesentlichen eine 2D-Rotation in Bezug auf die und die Koordinaten durch, während die Koordinate unverändert bleibt.Rotation Transformation Matrix – onlinemath4allonlinemath4all. It turns out that the product (or composition) of two rotations is again a rotation, which agrees with the fact that the determinant of a product is the product of the determinants (or 1 in the case of a rotation).

Vector Rotations in 3D

How would I go about rotating a 3D matrix then? java; matrix; rotation; rotational-matrices; Share.This implies we can write the rotation matrix Rθ as a combination of the identity matrix I and matrix P : Rθ = (cosθ)I + (sinθ)P = (cosθ)(1 0 0 1) + (sinθ)(0 − 1 1 0) And we get the . Specifying the coordinates ( components) of vectors of this basis in its current (rotated) .

Rotation matrix for rotations around x-axis

There you rotate around a 4th dimensional axis. Matrix representation of a rotation in 3D. 1,014 6 6 gold badges 16 16 silver badges 36 .Mathematisch wird eine passive Drehung durch die Inverse der Drehmatrix, also D − 1 beschrieben. An explicit formula for the matrix elements of a general 3× 3 rotation matrix In this section, the matrix elements of R(nˆ,θ) will be denoted by Rij.Matrix representation of a rotation in 3D.

Rotation of Voxels in 3D Space using Python

We can rotate a vector counterclockwise through an angle \(\theta\) around the \(x\)–axis, the \(y\)–axis, or the \(z\)–axis.A basic rotation of a vector in 3-dimensions is a rotation around one of the coordinate axes. These functions create and manipulate 3D rotation matrices and rigid-body transformations as 3×3 SO (3) matrices and 4×4 SE (3) matrices respectively.float32, device=None) Generates a batch of random 3×3 rotation matrices, uniformly sampled according to the usual rotation metric. Asked 11 years ago.Rotation Matrix in 3D. θ − v y sin.

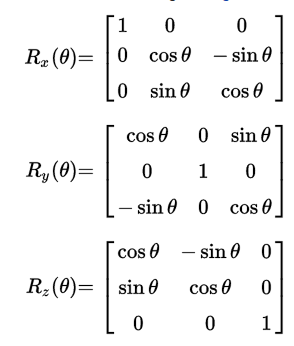
Need help implementing a 3D Rotation Matrix using NXOpen - Siemens: UG/NX - Eng-Tips

With rotation matrices we have nine parameters to represent a single rotation in 3D . Let w =v ×n2; that’s a unit vector lying in the second plane, perpendicular to v.3D Rotation Converter.In mechanics and geometry, the 3D rotation group, often denoted SO (3), is the group of all rotations about the origin of three-dimensional Euclidean space under the operation of . Sorted by: 248.We can compose rotations using multiplication, and the resulting matrix will remain a rotation matrix, in other words, all rotation matrices form SO(3) group under multiplication operation. However, manipulating 3D Rotations is always confusing, and debugging code that involves 3D rotation is usually quite time consuming.Rotation matrices are used in 3D and vector graphics, but you can’t multiply a 1000x1000x3 matrix (1Mpix RGB image) by a 2×2 rotation matrix. That is, physically rotating a vector by an angle θ leaves the length of the vector unchanged.Weitere Ergebnisse anzeigen

math

SO(3) group covers all possible rotations about the origin in 3D. Modified 5 years, 3 months ago. for rotation around an arbitrary point P, construct the following matrices: A: translation by minus P.Autor: Pen and Paper Science, game engines) –Rotation matrix: everywhere else (and the above) CSE 291, Spring 2021 5 The above-mentioned triad of unit vectors is also called a basis. θ] = [ v x cos.

3D Rotation Converter

Say you want to rotate a . v ′ = vR ( θ) = [ v x v y] [ cos.