Simplex Algorithmus Nebenbedingungen

Di: Luke

Zielfunktion und Nebenbedingungen. Es stehen zwei Eingabemöglichkeiten zur Verfügung und das Ergebnis kann unterschiedlich detailliert angezeigt werden. Gibt es also eine Lösung, muss nach Anwendungen des Simplex-A.

Seminar Algorithmen

Klassisches Transportproblem im Video zur Stelle im Video springen (00:34) Eine solche spezielle Struktur hat das sogenannte klassische Transportproblem.

Simplex-Algorithmus, Ablauf, Alternativer Ansatz, Lineare

Mit Offline-Funktion.Wie kann ich mithilfe des Simplex-Algorithmus folgendes Problem lösen? Dabei sollen alle vier Schlupfvariablen mitgeführt werden.

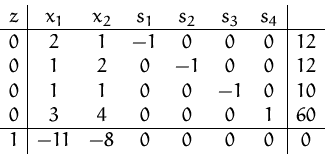
2-Phasen-Simplex-Algorithmus

Diese Probleme sind mit speziellen Lösungsverfahren effizienter zu bewältigen als mit dem Simplex-Algorithmus. Der primale Simplexalgorithmus kann hier natürlich auch angewandt werden, allerdings würde die Bestimmung der optimalen Lösung sehr rechenaufwendig sein.Lineare Optimierung grafische Lösung – GeoGebrageogebra. Bin total verwirrt.Mathematische Formulierung.Der Simplex-Algorithmus wurde von George Dantzig in den 1940er Jahren entwickelt und ist ein iteratives Verfahren zur Lösung von Problemen der linearen Programmierung. eine Variable kann unbegrenzt in die Lösung aufgenommen werden, der optimale Lösungswert wird unendlich 3.SIMPLE (Mathematik) Der SIMPLE-Algorithmus ( S emi- i mplicit M ethod for P ressure L inked E quations) wird in der numerischen Strömungsmechanik zur Lösung der Navier . Wenn man die Zahlen, die eigentlich das Problem beschreiben, also in .

Simplex-Algorithmus Schlupfvariable

Danach wenden wir den Simplexalgorithmus an und gelangen zum Endtableau: Dualer Simplex – Endtableau. Um ein spitzes Lösungspolyeder zu haben, betrachten wir LPs in Standard-Gleichungsform max ct x s.mit Hilfe des Simplex-Algorithmus bei Definition einer Zielfunktion sowie der Festlegung von Nebenbedingungen. Manchmal muss man aber eine Zielfunktion unter Nebenbedingungen minimieren (nicht maximieren; z. (Schlupfumformung, Pivotieren etc. Ax = b x 0 Das Finden einer Startlösung werden wir später behandeln. Dieses Video erlkärt das Thema Simplex-Algorithmus für Schüler und Studenten .In dieser Ausarbeitung möchte ich meinen Vortrag vom 18. Verfügbar für PC , Tablet & Smartphone . Das Werkzeug wendet den Simplexalgorithmus an.Lineare Optimierungsprobleme sind zu optimierende mathematische Probleme mit einer linearen Zielfunktion und linearen Nebenbedingungen.Man geht wie folgt vor: Lineares Optimierungsproblem in Standardform überführen (siehe vorherige Kapitel). Algorithmus bedeutet, dass man (Mensch oder Computer / . Es löst ein solches Problem nach . Die zu maximierende (minimierende) lineare Funktion heißt Zielfunktion. Es wird unterschieden zwischen dem .

Sonderfälle Simplexalgorithmus

orgSimplex Algorithmus MAX Programm – GeoGebrageogebra.2008 zum Thema „Der Simplex – Algorithmus: Formulierung, Beispiele und entartete Fälle“ zusammenfassen.

Wie Simplex Algorithmus mit vier Schlupfvariablen berechnen?

Und in der Tat geht die Formeldarstellung in diese Richtung.Zunächst wählen wir wieder Pivotzeile und -spalte aus: Dualer Simplex – Auswahl Pivotzeile und -spalte.Für die Anwendung des Simplex-Algorithmus müssen die Ungleichungen der Nebenbedingungen in ein Gleichungssystem überführt werden. z = z ( x, y) = d x + d y. Zuerst bringe ich das LP in Standardform: Nun einfügen von künstlichen Variablen und einführen der Hilfszielfunktion für Phase 1: Eine zulässige . Stell dir dazu drei Produktionsstandorte eines Herstellers vor und 4 . Und Basis für das Erfinden und spätere Ausführen einer solchen Vorschrift ist, dass das Problem formalisiert dargestellt werden kann. Struktur der Probleme.

Simplex Algorithmus: Erklärung und Beispiel · [mit Video]

Rolf Stahlberger. Die Standardform muss dann in die Normalform überführt werden (Gleichheitsbedingung) mittels Einführung von Schlupfvariablen. x0 >= 0 lautet, ist die optimale Lösung der Zielfunktion bestenfalls 0. Bei der in diesem Unterprogramm eingebundenen Methode . 184 views 5 months ago Lineare Optimierung. Mit dem Simplex-Algorithmus konnte man folgendes Optimierungsproblem lösen: eine Zielfunktion wurde unter Nebenbedingungen (Beschränkungen) maximiert. Beispiel: Angenommen, du musst die Produktion von zwei .

Simlpex-Algorithmus: Einführung

netDas Simplexverfahren der linearen Optimierung einfach .Simplextableau aufstellen, Simplex-Algorithmus/-VerfahrenWenn noch spezielle Fragen sind: https://www. Die Grundidee des Simplex-Verfahrens wurde 1947 von George Dantzig vorgestellt .Rechner Simplexalgorithmus. Der Simplex-Algorithmus navigiert iterativ entlang der Kanten eines geometrischen Lösungsraums (Simplex), um die Ecke mit dem optimalen Wert der Zielfunktion zu finden. Er kommt zur Anwendung wenn es mehrere Engpässe für eine Produktion gibt.Der Simplex-Algorithmus dient der Bestimmung der Entscheidungsvariablen eines linearen Optimierungsproblems unter Berücksichtigung von Nebenbedingungen.Aber zu deiner Drei-Phasen-Methode solltest du noch ein paar Erläuterungen liefern, oder zumindest einen Link woher das stammt. Zur Beschreibung des Vorgehens müssen zwischendurch immer wieder einige Begrifflichkeiten geklärt werden. Ein Algorithmus ist eine Rechenvorschrift.

Simplex Algorithmus

Rechner Simplexalgorithmus

Bestimmen Sie die optimalen Werte für x,y und z unter gegebenen Nebenbedingungen. Lineares Programm (LP) besteht aus folgenden Bestandteilen: Zielfunktion. Simplex-Algorithmus – unbeschränkt Ein lineares Programm LP ist unbeschränkt, wenn die Nebenbedingungen den Umfang nicht ausreichend . Das optimale Endtableau ist gegeben mit: x 1 = 5 2, x 2 = 3 4 .Ein Simplex-Verfahren (auch Simplex-Algorithmus) ist ein Optimierungsverfahren der Numerik zur Lösung linearer Optimierungsprobleme, auch als Lineare Programme (LP) . Phase : Finden einer zulässigen Basis. Standardform: Minimierungsproblem.Simplex-Algorithmus. Es löst ein solches Problem nach endlich vielen Schritten exakt oder stellt dessen Unlösbarkeit oder Unbeschränktheit fest.Die Standardform muss dann in die Normalform überführt werden (Gleichheitsbedingung) mittels Einführung von Schlupfvariablen.

Mathematische Optimierung von Ernährungsaufgaben

Hierzu werden die Schlupfvariablen x n + 1,.Um den primalen Simplex-Algorithmus anwenden zu können, muss das lineare Optimierungsproblem in Standardform vorliegen. Übungsaufgabe: 3 Nebenbedingungen mit Basislösung. Zum Video: Begriffe. Nebenbedingung, Nichtnegativitätsbedingung) 2.

Simplex-Algorithmus

Simplex-Verfahren | Studydrivestudydrive.

Simplex Algorithmus: Erklärung und Beispiel · [mit Video]

Der Simplex-Algorithmus.Mit dem Verfahren des dualen Simplex-Algorithmus (eigentlich) auch nicht, allerdings habe ich eine Frage zur Umformung.Duales Problem Definition.Der Simplex-Algorithmus Voraussetzungen: Wir brauchen einspitzes Polyeder.Nebenbedingung u.

Beispiel: Revidierter Simplex-Algorithmus

Maximierungsprobleme müssen in die Standardform überführt .

Varianten und Verbesserungen des Simplex-Verfahrens

Video: Begriffe. Die Relaxation von Nebenbedingungen führt auf die Lagrange-Funktion, das Konzept des dualen Problems und darauf abgestimmte Lösungsmethoden.

Zwei-Phasen-Simplex

Es handelt sich bei dem Simplex Algorithmus (SA) um keine Annäherungsmethode, obwohl die benutzten Nebenbedingungen und die Zielfunktion oft nur als Linear approximiert werden.Das Simplex-Verfahren (auch Simplex-Algorithmus) ist im Operations Research ein Optimierungsverfahren zur Lösung linearer Programme (LPs).

Simplex-Algorithmus - verständlich erklärt! - YouTube

Simplex Algorithm: Example I First tableau: x3 = 1 + x1 x2 x4 = 3 x1 x5 = 2 x2 z = x1 + x2 Replace 3 by 2 in the basis B: B = f2;4;5g: x2 = 1 + x1 x3.Es geht darum, die bestmögliche Lösung zu finden, die die Zielfunktion maximiert oder minimiert und gleichzeitig alle gegebenen Nebenbedingungen erfüllt. Der Simplex-Algorithmus löst lineare Optimierungsprobleme. Wir müssen einStartlösungﬁnden. Bei der in diesem Unterprogramm eingebundenen Methode handelt es sich um ein Optimierungsverfahren zur Lösung linearer Optimierungsprobleme, bei welcher relevante Nebenbedingungen in Form linearer Ungleichungen aufzustellen .Mit Hilfe des Simplex-Algorithmus lassen sich lineare Gleichungssysteme unter Nebenbedingungen lösen: Hier können Sie die aktuelle Version(2. die dritte phase des simplex algorithmus, die braucht man dann wenn bei den nebenbedingungen nicht alle x >= 0 sein müssen sondern eins oder mehrere x = 0, dann muss man in phase 1 die . Die in der Zielfunktion auftretenden Variablen ( x, y) heißen Entscheidungsvariablen. Tatsächlich zeigten Borgwardt und andere in den 1980er Jahren, dass solche Fälle wie der Klee-Minty-Würfel extrem selten sind und dass einige Varianten des Simplex-Algorithmus unter bestimmten Annahmen an den Input im Mittel nur . Hier wird der Simplex-Algorithmus leicht verständlich, anschaulich und strukturiert an einem Beispiel mit zwei Variablen und drei . Lernen Sie effektiv & flexibel mit dem Video Lineare Optimierung – Simplex Algorithmus aus dem Kurs Lineare Algebra Grundlagen.Zur Anwendung des Simplex Verfahrens benötigt man folgende Elemente: Die Zielfunktion, welche optimiert werden soll; Die gegebenen Nebenbedingungen, welche die .Simplex-Algorithmus, Ablauf, Alternativer Ansatz, Lineare OptimierungWenn noch spezielle Fragen sind: https://www.ich habe irgendwo gelesen, dass es drei Sonderfälle beim Simplex-Algorithmus gibt: 1.

Demo Simplex Algorithmus - YouTube

Der Simplex-Algorithmus Wir wollen das folgende LP .Die Anzahl der Nebenbedingungen ist größer als die Anzahl der Variablen. Als erstes muss man das lineare Gleichungssystem aufschreiben, d. Zum Video: Vorgehen + Beispiel. Es sind keine negativen Werte mehr auf der rechten Seite gegeben.Als Lösungsverfahren für lineare Optimierungsprobleme werden der Simplex-Algorithmus und das Branch-and-Bound-Verfahren vorgestellt und anhand eines Beispiels erläutert.Eine der wichtigsten mathematischen Methoden zur Unterstützung von Entscheidungen ist der Simplex-Algorithmus.de Playlists zu allen Mathe-Themen findet i. Die lineare Programmierung ist eine mathematische Technik zur Optimierung einer linearen Zielfunktion, die linearen Gleichheits- und . Hier ist es plötzlich keine Einheitsmatrix mehr sondern die letzte Zeile sind alles nullen? Und jetzt weiss ich nicht mehr wie das mit den Schlupfvariablen geht.Der Simplex-Algorithmus, oder auch Simplexverfahren genannt, ist eine Möglichkeit lineare Ungleichungen zu lösen und dessen Maximum anzugeben. Standardform in Normalform überführen: Hierfür muss die Ungleichheitsbedingung ≤ der Standardform in eine Gleichheitsbedingung = umgeformt werden.Das Simplex-Verfahren (auch Simplex-Algorithmus) ist ein Optimierungsverfahren der Numerik zur Lösung linearer Optimierungsprobleme.

Simplex-Verfahren: Erklärung & Anwendung

Folgende Zielfunktion Z = − 2 x − 4 y + z soll unter . Erster Schritt: Ein lineares Programm schreiben.Simplex-Algorithmus Definition.de Playlists zu allen Mathe-The.Simplex-Algorithmus Schlupfvariable. x* =, y* =, z* = Übungsaufgabe: 3 Nebenbedingungen mit Basislösung. Meist habt ihr dann .Der Simplex-Algorithmus ist ein populäres Verfahren zum Lösen von Aufgaben der linearen Optimierung. Nebenbedingungen (Restriktionen) Mit diesem Werkzeug können Lineare Optimierungsprobleme (LP) online gelöst werden.orgEmpfohlen auf der Grundlage der beliebten • Feedback

Simplex-Verfahren » Definition, Erklärung & Beispiele

Phase : Simplex mit dieser Basis als Startbasis. Und zwar lautet ja der erste Schritt beim dualen Simplex-Algorithmus, dass man nur noch ≤ -Resitriktionen haben darf: Bei den ersten beiden Nebenbedingungen ist das auch kein Problem: I −x1 − 2×2 ≤ −6.Dieses Video erlkärt das Thema Simplex-Algorithmus für Schüler und Studenten. alternative Lösungen sind möglich 2. $$ Nebenbedingungen: $$ x\le10 $$ $$ y\le7 $$ $$ x+y\le13$$ $$ 12x+32y\le256$$ x,y und die Schlupfvariablen sollen nicht negativ sein. Zielfunktion: $$ Z(x,y) =100x + 160y \Rightarrow max.Voraussetzung für die Anwendung des primalen Simplex-Verfahrens: Es muss die Standardform vorliegen (Maximierungsproblem, Kleiner/Gleich-Nebenbedingung, Nichtnegativitätsbedingung).

Simplex Algorithm: An Example

Die optimale Lösung wird dabei iterativ (d.

Lineare Optimierung

bis jetzt ganz gut zurecht, bis diese Aufgabe kam. Es löst ein solches . Bevor ich den Simplexalgorithmus explizit formuliere, möchte ich an dieser Stelle zunächst noch einmal das Beispielproblem vor Augen führen, das in der zugrunde liegenden .In der Praxis hängt die Laufzeit des Simplex-Verfahren oft im wesentlichen linear von der Anzahl der Zeilen ab., x N eingeführt.deEmpfohlen auf der Grundlage der beliebten • Feedback

Simplex-Verfahren

Second tableau: x2 = 1 + x1 x3 . Dies wird mit Hilfe von . beim Zweiphasensimplex besteht eine Inkonsistenz der Nebenbedingungen (wenn die . Mittels des Algorithmus der oberen Schranken ist das Problem bereits im oben genannten Abschnitt bestimmt .Meine Frage: Löse das folgende LP mit dem Zwei-Phasen Simplex Algorithmus Meine Ideen: 1.Das Simplex-Verfahren ist besonders effektiv bei Problemen mit vielen Variablen und Nebenbedingungen.

The Simplex algorithm - a quick summary - YouTube

Ich kam mit dem Simplexa.

QVOC

Music