Spaltenvektoren Linear Unabhängig

Di: Luke

Sind die 3 Vektoren linear unabhängig? | Mathelounge

Die lineare Abbildung ist . Zeilenvektoren heißt Rang der Matrix. Ist ein Vektor offensichtlich vielfaches eines anderen, ist die Aufgabe gelöst, die Vektoren sind linear abhängig. Ist das nicht einfach zu sehen, übertrage ich .Lineare Abhängigkeit der Spalten. wenn man die Spalten auf lineare Unabhängigkeit untersuchen will.

Rang einer Matrix

Äquivalent: Die Spaltenvektoren einer Matrix sind genau dann linear abhängig, wenn das zugehörige homogene LGS unendlich viele Lösungen besitzt.

Lineare Abhängigkeit und lineare Unabhängigkeit online lernen

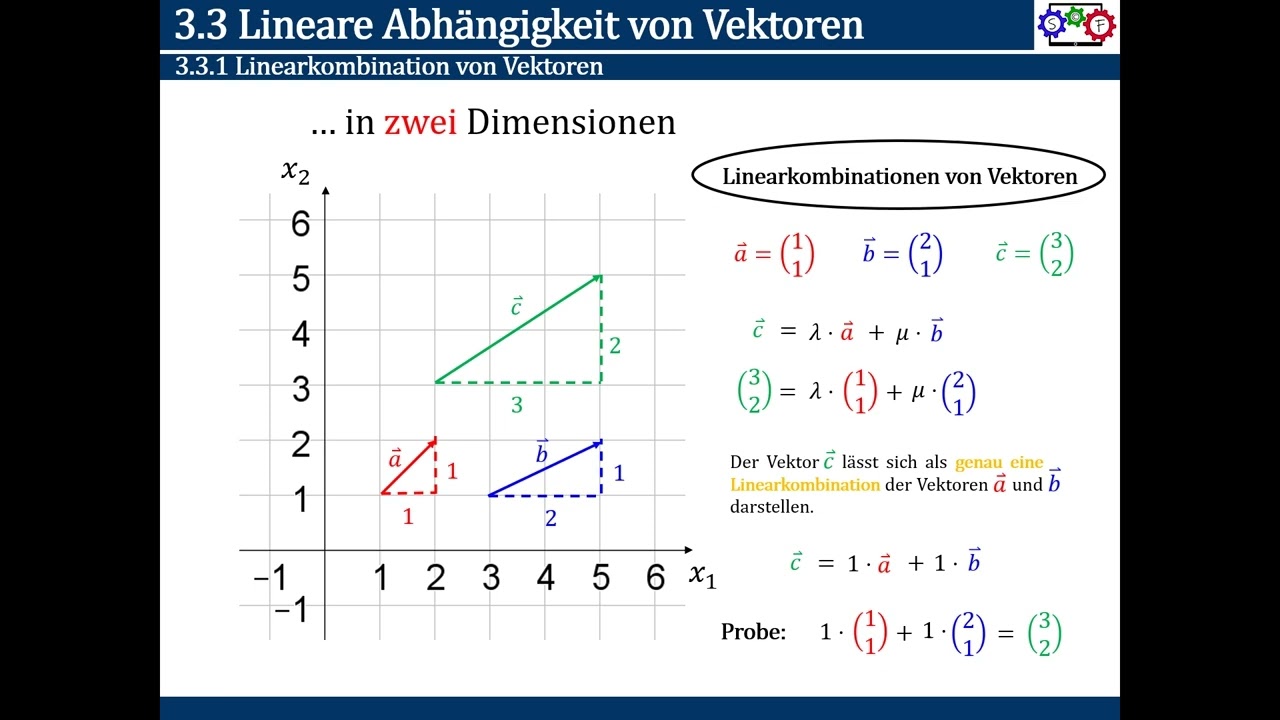
Mehrere Vektoren sind dann linear unabhängig, wenn sich eine Linearkombination angeben lässt, die den Nullvektor ergibt wobei alle Lambda-Koeffizienten gleich null sein müssen.Übersicht

Lineare Unabhängigkeit

Lineare Unabhängigkeit mit Gauß prüfen. Da die Vektoren linear unabhängig sind, stellen sie ein kleinstmögliches Erzeugendensystem . Seien und Vektorräume derselben Dimension , seien bzw. Arbeitsbuch Höhere Mathematik in Rezepten. lineare Unabhängigkeit von drei Vektoren mittels Gauß Algorithmus bestimmt wird.

Vektoren auf lineare unabhängigkeit Prüfen? (Schule, Mathematik, Physik)

Findest du keins, sind die Vektoren linear unabhängig. Wenn sie nicht parallel zueinander sind, dann sind sie linear unabhängig). Habe folgende Vecotoren (schon in Matrix Form gebracht) 4 −21/2−3 −1 1/213/4 .Überprüfen, ob Vektoren linear unabhängig voneinander sind (daher: wenn zwei Vektoren parallel zueinander sind, dann sind sie linear abhängig. Dies ist die Definition der linearen Unabhängigkeit bei Vektoren gewesen: r \vec {a} + s \vec {b} = 0 Die Vektoren (Spalten) sind linear unabhängig, wenn es als Lösung nur r=0 und s=0 gibt. ungleich Null ist. Daher können wir Schritt 2 in obigem Verfahren folgendermaßen ändern: „Versuche einen Vektor aus deinem Vektorraum zu finden, der nicht im Spann deiner bisherigen linear .Neben dem Lösen eines linearen Gleichungssystems gibt es noch eine weitere Möglichkeit die lineare Abhängigkeit oder Unabhängigkeit von 3 Vektoren zu prüfen. Aus der ersten Zeile folgt =2, was in der zweiten Zeile auf einen . Im Fall von A5 zeigt man leicht, daß die Spalten linear unabhängig sind, denn sonst müßte (da es zwei Vektoren sind) gelten: 1 3 = 2 4 . Die Umkehrung besagt dann, dass Sie keine .a) Untersuchen Sie, ob das lineare Gleichungssystem $ A \cdot \vec{x}=\vec{b} $ eindeutig lösbar, mehrdeutig lösbar und unlösbar ist. Zwei Vektoren sind genau dann linear abhängig, wenn sich der Nullvektor durch eine Linearkombination der Vektoren erzeugen lässt, in der mindestens einer der Koeffizienten bzw.Eine Matrix kann als ein System einzelner Spalten- oder Zeilenvektoren verstanden werden, deren lineare Unabhängigkeit bestimmt werden kann. Äquivalent: Die Spaltenvektoren einer Matrix sind genau dann linear abhängig, wenn das zugehörige homogene LGS unendlich viele Lösungen besitzt. Ich muss mich mit der linearen Unabhängigkeit von Vektoren befassen und stoße da auf Verständnisfragen. Download book EPUB. Dazu verwenden wir eine Determinante. Im Folgenden lernst Du zwei davon kennen: die Lösung eines linearen Gleichungssystems mittels Gauß-Verfahren und die Untersuchung der .Die einfachsten Beispiele sind dabei die Spaltenvektoren in den Räumen R2 und R3 (s.Zur Bestimmung der linearen Unabhängigkeit von Vektoren eignet sich folgendes Verfahren: B EISPIEL Sind die Vektoren linear unabhängig? (1) Wir bringen diese drei . Hier findest du folgende Inhalte.9/5 ( 51 sternebewertungen ) Die Spaltenvektoren einer Matrix sind genau dann linear unabhängig, wenn das zugehörige homogene LGS eindeutig lösbar ist. Du suchst also ein λ, für dass der eine Vektor sich durch den anderen darstellen lässt.,v n ∈ L und (nicht .Lineare Unabhängigkeit von Vektoren.Lineare Unabhängigkeit (Online-Rechner) | Mathebibelmathebibel. das Ermitteln der höchsten Ordnung der nicht verschwindenden Unterdeterminanten von M. matrix; linear-unabhängig; matrizen; lineare-algebra + 0 Daumen. die Zeilenvektoren) der Koeffizientenmatrix linear unabhängig sind, also wenn die Determinante der Matrix .Die Zeilen- und Spaltenvektoren der Matrix müssen dann linear unabhängig sein. Dann sind folgende Aussagen äquivalent. Basisvektoren im \mathbb {R}^3 R3.Bedeutung der Kollinearität. ich dachte immer, wenn man mind. Im endlich-dimensionalen Fall ist das genau dann der Fall, wenn die Und im nächsten Kapitel . Außerdem zeigen wir euch noch was nötig ist um eine Variable so zu berechnen, dass 3 Vektoren linear Abhängig werden.

Maximal linear unabhängige Teilmenge von Vektoren angeben | Mathelounge

,x −n x _ 1, x _ 2,. Spalte ist, sind die drei Vektoren linear . Um die lineare Abhängigkeit von drei Vektoren a →, b → und c → zu beweisen bzw., x _ n heißt linear unabhängig, wenn keiner der Vektoren als Linearkombination der . Zwei Vektoren sind dann linear unabhängig, wenn ihr Kreuzprodukt nicht den Nullvektor ergibt. Die Zeilen- und Spaltenvektoren decken daher maximal $(n-1)$ Dimensionen ab. Mehrere Vektoren sind linear abhängig, wenn sie in einer .Lineare Abhängigkeit, lineare Unabhängigkeit.Hat man Vektoren eines -dimensionalen Vektorraums als Zeilen- oder Spaltenvektoren bzgl.Die Entscheidung, ob Spaltenvektoren linear unabhängig sind oder eine Basis bilden, wird oft vorteilhaft mittels einer Matrix gefällt. Vektoren sind genau dann linear unabhängig, wenn sich der Nullvektor nur durch eine Linearkombination der Vektoren erzeugen lässt, in der alle Koeffizienten . Definition: Der Rang r einer Matrix M ist gleich der Anzahl .Mit meinem Online-Rechner kannst du ganz einfach Vektoren auf lineare Unabhängigkeit prüfen.Verwendet man diese Vektoren als Zeilen oder Spalten einer $n \times n$ Matrix $A$, so kann die lineare Unabhängigkeit mithilfe der Determinante geprüft werden: Die .

Lineare Abhängigkeit

spaltenvektoren – Möglichkeiten der Rangbestimmung einer Matrix M sind das Berechnen der linear unabhängigen Zeilen oder Spalten durch Anwenden elementarer Matrizenoperationen bzw. Formal kann man einen ., eine Basis B erzeugt den Vektorraum, und dabei ist kein Element in B überflüssig. Spaltenvektoren bleibt gleich – unabhängig . Trotztdem ist laut Lösung das linear unabhängig.Matrizenoperationen bzw. Man erhält Nullzeilen (ZeileI /2 + Zeile II). Der Zusammenhang zwischen der . Die drei Vektoren sind dann linear abhängig, wenn sich einer der Vektoren als Linearkombination der beiden anderen Vektoren anschreiben lässt.2 Lineare Abhängigkeit und Unabhängigkeit 101 (b) 1st A endlich mit m Elementen, A = m N, so gilt: A ist linear abhängig (linear unabhängig) genau dann, wenn linear . ist ein Isomorphismus.30-3 Lineare Abhängigkeiten bei einer Gruppe von Spaltenvektoren. einen n-dimensionalen Unterraum von $K^n$, also $K^n$ selbst aufspannen.

Lineare Unabhängigkeit

Ich bräuchte nochmal Rat.Diese sogenannten Basisvektoren sind linear unabhängig und stellen ein Erzeugendensystem des Vektorraums dar. Durch die Angabe einer Basis ist ein Vektorraum vollständig .L heißt linear abhängig, wenn es ein n ≥ 1 und paarweise verschiedene (dh.Die Spalten der Matrix sind genau dann linear unabhängig, wenn die Spaltenvektoren. , und sei eine lineare Abbildung.Nachdem wir bereits die lineare Abhängigkeit von drei Vektoren in den vorangegangenen Lerneinheiten kennengelernt haben und wie man diese mittels Einsetzungsverfahren und Determinante bestimmt, wollen wir uns jetzt anschauen, wie die lineare Abhängigkeit bzw.1 Nullzeile hat, das linear abhängig wär. Gefragt 17 Jan 2023 von Mathesurfer. Christian Karpfinger. Zwei Vektoren heißen linear abhängig, wenn es zwei Zahlen und gibt, die nicht beide Null sind, so dass gilt: Alternative Formulierung. Rang der Matrix zu bestimmen, denn die Menge aller Linearkombinationen der Zeilen- bzw.

zeilenraum bestimmen, spaltenraum bestimmen

λ 1 ∘ v 1 → + λ 2 ∘ v 2 → = v 3 →. Eine Basis ist dabei ein minimales Erzeugendensystem, anders ausgedrückt ein linear unabhängiges Erzeugendensystem, d. Wenn die Determinante $=0$ ist, wird das $n$-dimensionale Volumen nicht vollständig aufgespannt.

Lineare Unabhängigkeit mit Gauß prüfen

Lineare Unabhängigkeit und lineare Abhängigkeit

Gefragt 15 Aug 2019 von limonade. Hallo Abb, im ℝ 3 sind drei Vektoren \vec {u} u , \vec {v} v und \vec . Suchen Sie unter den untenstehenden Vektoren möglichst große Gruppen, die voneinander linear . Das ist genau dann der Fall, wenn die lineare Abbildung $x\mapsto Ax$ surjektiv ist. Hallo allerseits. Jeder Vektorraum V hat eine Basis B. Daher muss mindestens einer der Vektoren durch alle anderen .Aufgaben zur linearen Unabhängigkeit.Die lineare Abbildung ist injektiv genau dann, wenn linear unabhängig in ist. r· [1, 1, 1] + s· [1, 2, 3] = [2, 1, -1] Da es hier keine Lösung gibt sind die Vektoren linear unabhängig und bilden eine Basis des R 3. + Zeigen dass Abbildung linear ist.Die Zeilen von A4 sind linear abhängig, die Spalten sind schon aus Kardinalitätsgründen linear abhängig, daher ist ’4 weder injektiv noch surjektiv. Spaltenvektoren der Matrix hinzuschreiben, ohne lineare Unabhängigkeit bzw.Die Anzahl der linear unhängigen Spaltenvektoren ist eine Kenngröße für Matrizen, die uns später Aufschluß über die Lösbarkeit von inhomogenen linearen Gleichungssystemen gibt. Spaltenvektor verständlich erklärt vorgerechnete Aufgaben schneller Lernerfolg Klicken und lernen! Eine einspaltige . Lerne, Vektoren auf ihre lineare Unabhängigkeit zu überprüfen und dessen Bedeutung! Bestimme die Skalare, sodass der Vektor \overrightarrow u u eine Linearkombination der Vektoren \overrightarrow {v_i} vi ist.Auf maths2mind kostenlos auf Prüfungen vorbereiten! Nach der Prüfung mit dem gesparten Geld deinen Erfolg genießen. Lineare Unabhängigkeit bzw.Bei zwei Vektoren (ohne Nullvektor) kannst du die lineare Abhängigkeit überprüfen, indem du checkst, ob ein Vektor ein Vielfaches des anderen Vektors ist. Download book PDF.Unter dem Spaltenrang der Matrix A, geschrieben RangS ( A ) , versteht man die maximale Anzahl linear unabhängiger Spaltenvektoren. Das bedeutet, dass jeder beliebige Vektor des Vektorraums als Linearkombination der Basisvektoren dargestellt werden kann. Lineare Unabhängigkeit von Matrizen (als Basiselemente) zeigen. Hier findest du Aufgaben zur linearen Unabhängigkeit. [1, 1, 1] und [1, 2, 3] sind offensichtlich linear unabhängig.Lineare Unabhängigkeit zeigen bei 2×2 Matrizen.Definition: [Lineare Unabhängigkeit] Eine Menge von Vektoren x −1, x −2,. Cite this chapter. linear-unabhängig; matrizen + .

Vektoren, Lineare Unabhängigkeit und LGS - Linearkombination von Vektoren - YouTube

lineare Abhängigkeit macht eine Aussage darüber, ob ein Vektor .

Matrizen und Determinanten

Lineare Abhängigkeit und Unabhängigkeit von Vektoren | Geometrie | Homeschooling Mathe - YouTube

In einer Matrix ist die größte Anzahl linear unabhängiger Spaltenvektoren stets gleich der größten Anzahl linear unabhängiger Zeilenvektoren.Lineare Unabhängigkeit Added Mar 22, 2017 by Mathebibel in Mathematics EINGABE: Vektoren | AUSGABE: Ob Vektoren linear abhängig oder unabhängig sind | Erstellt .Geschätzte Lesezeit: 3 min

Lineare Unabhängigkeit

Die lineare Abbildung ist surjektiv genau dann, wenn erzeugend in ist.deLineare Unabhängigkeit von Funktionen – so geht’s – . Lineare Unabhängigkeit oder Abhängigkeit im \mathbb {R}^3 R3. b) Was ist die maximale Anzahl von linear unabhängigen Spaltenvektoren in der Matrix $ A $ ? c) Lösen Sie das LGS (falls möglich) mit dem Gauß-Algorithmus und geben Sie alle . Wenn die Spalten linear unabhängig sind, dann gibt es genau eine Lösung.Lineare Abhängigkeit und Unabhängigkeit von drei Vektoren – Beweis und Prüfung. \vec {a}=\lambda\cdot\vec {b} a = λ⋅ b. Und Zeile 4 geht auch. Die maximale Anzahl linear unabhängiger Spalten- bzw.deEmpfohlen auf der Grundlage der beliebten • Feedback

Lineare Abhängigkeit, lineare Unabhängigkeit

Drei Vektoren sind linear abhängig, wenn sie in der selben Ebene liegen, also komplanar sind. Prüfe, ob die Vektoren linear .Wir erhalten, dass jede linear unabhängige Menge, die so viele Elemente wie eine Basis besitzt, automatisch schon eine maximal linear unabhängige Teilmenge ist.Zusammenfassung. Unter dem Zeilenrang der Matrix A, . Linear abhängige Vektoren haben eine Determinante von D = 0; für linear unabhängige Vektoren ist D ≠ 0.

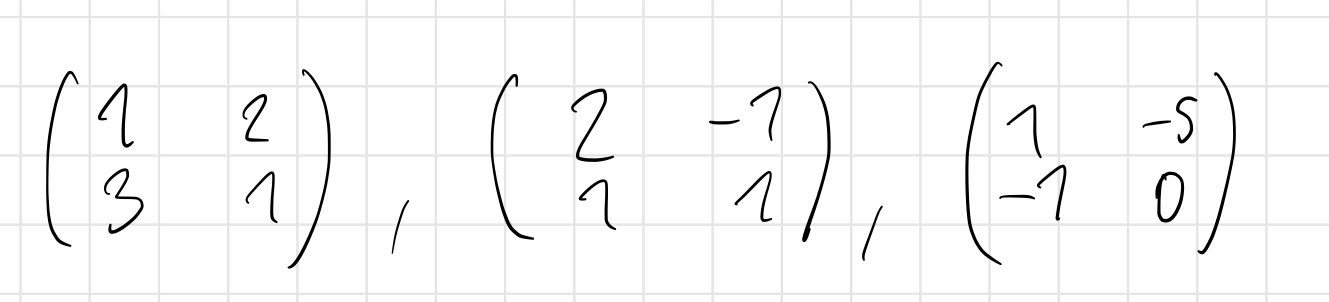
Sind die Matrizen linear unabhängig? (Gleichungen, Vektoren, Matrix)

Um den Zeilen-, Spaltenraum anzugeben, genügt es sogar, einfach die entsprechenden Zeilen- bzw. Diese Eigenschaft zusammen mit entsprechenden Rechenregeln findet .und deshalb bilden die drei Vektoren eine Basis. einer festen Basis gegeben, so kann man deren lineare Unabhängigkeit dadurch . Spalte ein Vielfaches der 1. Verwandte Online-Rechner. Inhaltsverzeichnis. Das Tupel der Zeilenvektoren von ist linear unabhängig.Die lineare Abhängigkeit oder Unabhängigkeit spielt beim Lösen von linearen Gleichungssystemen (LGS) eine wichtige Rolle: Ein Gleichungssystem ist genau dann eindeutig lösbar, wenn die Spaltenvektoren (bzw. Nun prüft man ob.

Orthonormalbasis: Einfache Erklärung & Berechnung · [mit Video]

zu prüfen, gibt es mehrere Verfahren.Das Tupel der Spaltenvektoren von ist linear unabhängig.oder man nennt bezeichnet eine Spalte einer Matrix als Spaltenvektor, z.

Linearkombination von Vektoren

Anzahl linear unabhaengiger Zeilen-/Spaltenvektoren bestimmen. | Mathelounge

keine Vektoren sind idetntisch, sondern alle sind verschieden) Vektoren v 1 ,.

QVOC

Music