QVOC

Music

Surjektive Funktion Beispiel | Surjektivität: Definition & Beispiele

Di: Luke

Die Menge der reellen Zahlen wird hier mit bezeichnet, die Menge der nichtnegativen reellen Zahlen mit . Da die Funktion x^4-5 x4 −5 jedoch stets \ge-5 ≥ −5 ist, wird zum Beispiel der Wert -6 −6 aus der Zielmenge \mathbb {R} R nicht erreicht.

Surjektion, Surjektivität

Häufigkeit: ⓘ.Wichtige Rechenregeln für Funktionen Definitionsbereich Wertebereich Wertetabelle Mehrstellige Funktionen Funktionen verketten Umkehrfunktion Surjektive Funktionen Injektive Funktionen Bijektive Funktionen Als Funktion f, bzw. Gibt es einen ganz einfachen .Injektivität und Surjekivität bei verknüpften Funktionen | . id N: N → N;y 7→y. injektiv und surjektiv. Und f ist surjektiv auf B, wenn jede Waagrechte der Ebene, die die Menge B der y-Achse trifft, den Funktionsgraphen in mindestens einem Punkt schneidet. Es gibt zu jedem x-Wert genau einen y-Wert.Funktion auf IN die surjektiv aber nicht injektiv ist. StudySmarterOriginal!Formal ausgedrückt: Eine Funktion f: A → B ist surjektiv, wenn für jedes Element y ∈ B mindestens ein Element x ∈ A existiert, so dass f ( x) = y. Die Surjektivität einer Funktion f\colon\, A \to B f: A → B hängt nicht nur vom Funktionsgraphen \ { (x,f (x)) \mid x \in A\}, {(x,f (x)) ∣ x ∈ A}, sondern auch von der Zielmenge B B abhängt (im Gegensatz zur . Die Funktionen in der ersten Reihe sind surjektiv, die in der zweiten . Geben Sie ein Beispiel für eine Funktion von N nach N an, die surjektiv aber nicht injektiv ist. Bei einer injektiven Abbildung gibt es zu jedem Element b\in B b ∈ B höchstens ein Element a\in A a ∈ A mit b=f (a) b = f (a). Die Menge der Funktionen in einen Körper, die an einer Stelle 1 und sonst 0 sind, ist linear unabhängig.Eine surjektive Funktion kann wie folgt definiert werden: Eine Abbildung zwischen den zwei Mengen A und B heißt surjektiv, wenn zu jedem mindestens ein mit existiert.

Beispiele: injektiv, surjektiv, bijektiv

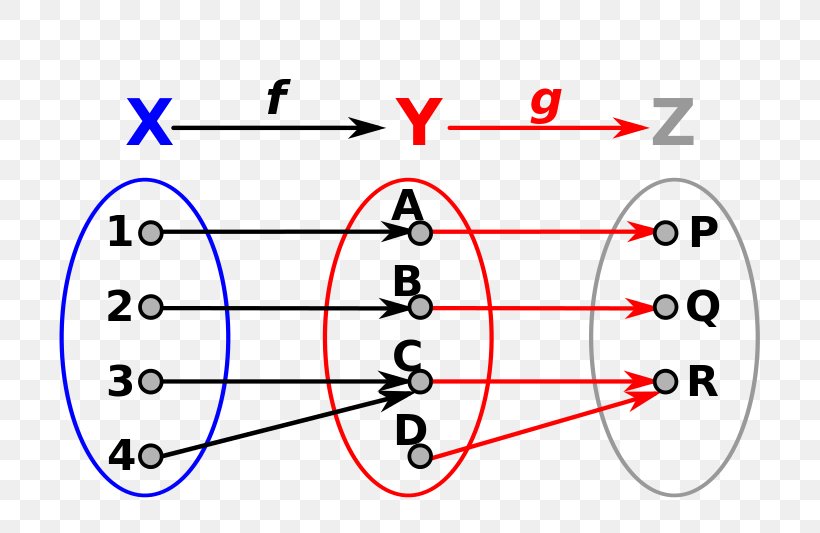
In Abbildung 12. Die Definition von Surjektiv lautet nämlich: Bld = Wertevorrat.Kapitel 1: Aussagen, Mengen, Funktionen Surjektive, injektive und bijektive Funktionen. g 1: R !R, x7!x2 ist nicht surjektiv (es wird kein Wert kleiner 0 getro en). Die Funktion, die jedem Osterreicher seine Passnummer zuordnet nicht surjektv (wenn man alle naturlichen Zahlen als Wertebereich zul asst).Beispiele: injektiv, surjektiv, bijektiv. bei reellen Funktionen praktisch vor. Er bezeichnet eine spezielle Eigenschaft von Abbildungen und Funktionen.Bijektive Funktion.Eine Surjektive Funktion ist eine Funktion, bei der jedes Element der Wertemenge das Ergebnis eines Elements der Definition ist. Sei f :M →N eine Funktion. 2) ZIEL/ZWECK Die SuS können aufgrund des theoretischen Inputs und anhand von praktischen Beispielen erkennen, um welche Art der Funktion (SURJEKTIV, INJEKTIV oder BIJEKTIV) es sich .; Beispiel: Ordnet man jedem (monogam) verheirateten Menschen seinen Ehepartner bzw.

Surjektivität

Betrachte die Funktion f: R → .Bijektive Funktionen sind daher sowohl injektiv als auch surjektiv. Die identische Funktion auf einer Menge ist also die Funktion, die mit den Elementen Eine Funktion ist nicht injektiv, sondern treu.comEmpfohlen auf der Grundlage der beliebten • Feedback

Surjektivität: Definition & Beispiele

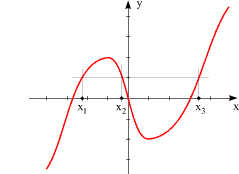
Sie ist nicht surjektiv (s. Wähle alle richtigen Antworten! Aussage 1: Es gibt Funktionen, die weder injektiv noch surjektiv sind; Aussage 2: Eine Funktion kann sowohl monoton steigende als auch monoton fallende Abschnitt beinhalten; Aussage 3: Jede Funktion muss entweder injektiv oder surjektiv oder bijektiv sein. Meine Frage: Hallo, ich habe grundsätzlich ein Problem Surjektivität zu beweisen. Nicht nur ihr könnt Deutsch mit eurem ewigen Hochpunkt statt Maximum; ich kann es auch. Dann heißt f surjektiv, falls die Gleichung f(x)=y fu¨r jedes y ∈ N mindestens eine Losung¨ x ∈ M besitzt, d.; Ebenso ist für die Funktion bijektiv mit der Umkehrfunktion . In unserem ersten Beispiel ist f(x) surjektiv, da jede gerade natürliche Zahl das Ergebnis einer natürlichen Zahl ist.Hier findest du Aufgaben mit Lösungen und Theorie zu: Injektiv, surjektiv, bijektiv. Die Funktion ist bijektiv mit der Umkehrfunktion . Die leere Funktion.In unserem ersten Beispiel ist f (x) injektiv, da jedem natürlichen Zahlen immer die nächstliegende natürliche Zahl zugeordnet wird.

Surjective Function Function Composition Injective Function Mathematics, PNG, 800x533px ...

(Es gibt kein x mit f (x) > 2) Sie ist nicht injektiv, weil es Elemente der Zielmenge gibt, Funktionswerte von mehr als einem x sein können.

Funktion und Umkehrfunktion

Bei deinem ersten Beispiel ist die Funktion surjektiv, da es zu jeder ganzen Zahl y y immer eine ganze Zahl x x gibt, so dass x = y-1 x= y −1. Das war doch, was . In formaler Schreibweise lautet die . Die Funktion mit ist surjektiv, denn keine reelle Zahl hat ein leeres Urbild. Bei uns gehört die 0 nicht zu den Natürlichen Zahlen. Ich weiß und ahne, dass sie Surjektiv ist, aber ohne den gelesenen Beweis hätte ich keine Idee, dies zu beweisen. Injektivität: Die Abbildung ist .Injektivität beweisenIn diesem Mathe Lernvideo geht es darum wie man die Injektivität einer Abbildung beweisen kann. Für injektive Funktionen lassen sich .Beispiele: Die Funktion, die jedem Osterreicher seinen Geburtstag (ohne Jahreszahl) zu- ordnet ist surjektiv. Injektiv Definition. Bei den folgenden Beispielen handelt es sich um surjektive Abbildungen: Die Abbildung f 1: N → N, n ↦ n ist surjektiv.Injektive Abbildungen. „Abbildung“, bezeichnen wir in der Mathematik eine Vorschrift f, die jedem Element x aus einer Menge . Definition: Was ist eine surjektive Funktion? Eine Funktion heißt surjektiv, wenn jeder Wert der Zielmenge mindestens einmal als Funktionswert vorkommt.

SURJEKTIV, INJEKTIV, BIJEKTIV

Geben Sie eine Funktion f:ℕ− > ℕ an, die surjektiv aber nicht injektiv ist.Ein Beispiel für eine surjektive Funktion im Alltag ist die Zuordnung von Geburtstagen zu Personen. aufgefaßt, so entsteht eine bijektive Abbildung. Und das ist die Sinusfunktion mit ihren unendlich vielen Perioden sicher auch nicht.Surjektivität bedeutet, dass bei einer Funktion jedes Element der Wertmenge mindestens einmal als Funktionswert angenommen wird.Eigenschaften von Funktionen.7 ist die Funktion f : X → Y bijektiv. Hier findest du folgende .

Surjektivität, surjektive Funktionen

f: N -> N (natürliche Zahlen) x -> (x-3)^2 surj. Weiterhin heißt f injektiv, falls die Gleichung f(x)=y fu¨r y .Die definierende Eigenschaft der Umkehrfunktion einer Funktion f : M → N war die Gleichung f(f−1(y)) = y f¨ur alle y ∈ N und diese kann man auch als f f−1 = id N lesen, wobei id N die sogenannte identische Funktion auf N ist, d. Eine Funktion f: M → N heißt surjektiv, falls .Funktionen lassen sich im Allgemeinen auf drei verschiedene Arten darstellen: als Wertetabelle, als Graph in einem Koordinatensystem, und.Beispiele: Die leere Menge ist linear unabhängig; nur der Nullvektor ist von der leeren Menge linear abhängig; ist der Nullvektor Element einer Menge, so ist diese linear abhängig. Jeder Tag des Jahres kann Geburtstag mindestens einer Person sein, aber jede Person hat genau einen Geburtstag. In unserem zweiten Beispiel ist f (x) .com/mathematrick/join ? ?MEIN KOMPLETTES EQUIPMENT https://mathematrick. Nachbemerkungen : Wird die Zuordnungsvorschrift des ersten Beispiels beibehalten, aber nicht als Funktion.Injektiv / Injektive Funktion: Bedeutung, Beispiel und Gegenbeispiel. Bei deiner Definition bin ich mir nicht ganz sicher.Intervall (-3, 3) .Geben Sie ein Beispiel für eine Funktion von N nach N an, die surjektiv aber nicht injektiv ist.Möglicherweise wurden bereits die Begriffe SURJEKTIV, INJEKTIV sowie BIJEKTIV anhand von Mengendiagrammen besprochen bzw. Wenn man die e-Funktion als Funktion von IR nach IR auffasst dann ist sie nicht surjektiv, weil zb -1 nicht getroffen wird.7: Bijektive Funktion f Beispiel. Beweis für Surjektivität gefragt, a.), da die negativen y-Werte keinem x-Wert zugeordnet sind.Surjektiv bedeutet, dass jedes Element der Zielmenge mindestens 1-mal erreicht werden muss. Die Umkehrfunktion von f(x) = e x ist die Logarithmusfunktion f(x) = ln x. Eine Abbildung kann injektiv, surjektiv oder bijektiv sein, je nach dem wie sie die Definitionsmenge auf die Wertemenge abbildet. Funktion bedeutet: Für jedes y (aus dem Wertebereich der Funktion) gibt es höchstens ein x (aus dem Definitionsbereich), das heißt nicht mehr als ein x, aber vielleicht auch keines. ist surjektiv, aber nicht injektiv. Dies wird im Folgenden für vier Funktionen \(A \aufrecht B\) dargestellt. Theorie: Injektiv, Surjektiv, Bijektiv. Surjektivität: Erklärung Beispiele Beweise – Verstehe alles schnell & einfach. Unterbegriffe: [1] bijektiv. • Falls f : M → N bijektiv ist, so gilt f(M) = N .Wie beweist man, dass eineAbbildung injektiv/ surjektiv ist . in Form einer . Man kann die Funktion surjektiv machen, indem man die . Ich erkläre euch an Beispielen wie man p. Beispiele: [1] Eine Abbildung ordnet jedem Element ihrer sogenannten Urbildmenge genau ein Element ihrer Zielmenge zu. algebra; injektiv; surjektiv; lineare-abbildung; Gefragt 1 Nov 2016 von L88. Injektive Funktionen kann man invertieren (deutsch: umkehren ).

Bijektive, injektive und surjektive Funktionen

Umfasst der Wertebereich die positiven reellen Zahlen .Beispiel: Die Funktion . Injektiv bei einer Abbildung bzw. Funktionswert 1 ist.

Onto function (Surjective Function) - Definition with examples

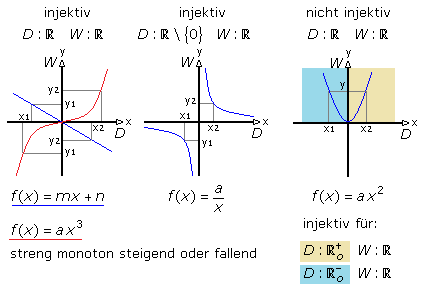
∀y ∈ N ∃x ∈ M :y =f(x). Eine Abbildung f:A \rightarrow B f: A → B, deren Umkehrung f^ {-1} f −1 wieder eindeutig ist, nennt man eineindeutig oder umkehrbar eindeutig oder injektiv.• F¨ur eine injektive Funktion f : M → N wird deren Umkehrfunktion f−1: f(M) → M definiert durch f−1(y) = x f¨ur y ∈ f(M), wobei f(x) = y.Es gibt vier mögliche injektive/surjektive Kombinationen, die eine Funktion besitzen kann.Surjektivität. Surjektiv ist sie nicht, weil es sich um eine Parabel . Eine Abbildung f f heißt surjektiv, falls es zu jedem y \in N y ∈ N mindestens ein x \in M x ∈ M mit y=f (x) y = f (x) gibt und damit f (M)=N f (M) = N gilt. nicht injektiv (weil zum Beispiel die Koordinate y=1 zwei x Koordinaten hat : 2 und 4) x -> 2x injekt.Für reelle Funktionen f : A → B existiert eine weitere anschauliche Interpretation: f ist injektiv, wenn jede Waagrechte der Ebene den Funktionsgraphen in höchstens einem Punkt schneidet.

surjektiv

Was bedeutet es, wenn eine Funktion / Abbildung surjektiv ist? Wie ist das Ganze definiert und wie kann man es sich z. Die Funktion ist daher nicht surjektiv. in eine einelementige Menge ist wohl das einfachste Beispiel einer nichtsurjektiven Funktion. Rechtschreibung. Man sollte besser schreiben: Surjektiv bedeutet dass es zu jedem Element y der Zielmenge mindestens ein Element x aus der Wertemenge gibt, welches auf .

Surjektive, injektive und bijektive Funktionen

Um zu zeigen, dass eine Funktion bijektiv ist und somit eine Umkehrfunktion besitzt, muss man zeigen, dass sie. Definition des Kronecker-Delta.

Surjektive, injektive und bijektive Funktionen.

? Siehe Algebra im Wiki 2 Antworten + 0 Daumen.Surjektivität nachweisen / widerlegen – surjektiv – Funktionen – BeispielIn manchen Klausuren wird nach dem Nachweis bzw.

Injektiv Surjektiv Bijektiv: Definitionen, Aufgaben und Beweise · [mit Video]

Sie ist nicht surjektiv, weil nicht jedes Element der Zielmenge R ein Funktionswert ist. Bijektivität (zum Adjektiv bijektiv, welches etwa ‚umkehrbar eindeutig auf‘ bedeutet – daher auch der Begriff eineindeutig bzw.deEmpfohlen auf der Grundlage der beliebten • Feedback Bei deinem zweiten Beispiel ist die Funktion nicht surjektiv, da es nicht zu jeder natürlichen Zahl y y eine natürliche Zahl x x gibt mit x = y -1 x = y−1.Ich suche eine Funktion die surjektiv ist, aber nicht injektiv ist. Für eine surjektive Abbildung gilt, dass der Wertebereich. Die Funktion f : ℝ→ ℝ x → x+1 ist injektiv: Es gelte . Man erhält dabei die . 1 -> 1, 2 ->1, 3 -> 2, 4 . Definition: Was ist eine injektive . Surjektivität beweisen. g 2: R !R+ 0, x7!x2 ist surjektiv.

Injektive und surjektive Funktionen

Werbefreiheit aktivieren. Nehmen wir als Beispiel die Funktion Z->Z:h (x) = x + 5.Auf diesen Beitrag antworten ».deInjektiv Surjektiv Bijektiv -> Wie kann ich Funktionen darauf . Ich habe mir überlegt, dass f (x):|x-3| sein könnte wobei im Definitionsbereich die 3 Ausgeschlossen wäre. nicht surjektiv (weil es kein n in N gibt, für das y=3 gibt) Stimmt das?

Bijektive Funktion

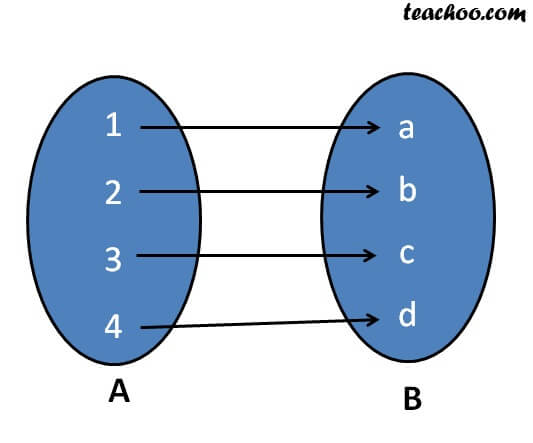
Und die WÄRE surjektiv.Jetzt Kanalmitglied werden und meinen Kanal unterstützen: https://www. Dieses Beispiel zeigt, daß die Menge R der reellen Zahlen und ein offenes Intervall im Sinne der Mengenlehre gleich groß (genauer: gleichmächtig) sind, denn eine Funktion dieses . Injektiv, surjektiv, bijektiv.deInjektiv, surjektiv, bijektiv, Schaubild mit Funktion – YouTubeyoutube. Die Funktionen in der ersten Spalte sind injektiv, die Funktionen in der zweiten Spalte sind nicht injektiv.

Surjective function - YouTube

Beispiele und Gegenbeispiele. Aussprache: ⓘ. Kein y-Wert kommt mehrmals vor. rechts) Anders gesagt: Kein Funktionswert darf mehrmals getroffen werden.In diesem Video erkläre ich euch graphisch anschaulich anhand zweier Beispiele was es für eine Funktion heißt surjektiv zu sein. Die leere Funktion in eine einelementige Menge ist das wohl einfachste Beispiel einer nichtsurjektiven Funktion.Komposition von injektiven, surjektiven oder bijektiven Abbildungen [Bearbeiten] Voraussetzung [ Bearbeiten ] f : A → B {\displaystyle f\colon A\to B} und g : B → C {\displaystyle g\colon B\to C} seien Abbildungen. f (2) = f (-2) => Linkseindeutigkeit ist verletzt.

Functions - Complete explanation and examples!

substantivisch entsprechend Eineindeutigkeit) ist ein mathematischer Begriff aus dem Bereich der Mengenlehre. ist surjektiv, . 1 2 3 4 a b c X Y d Abbildung 12. Die Abbildung f 2: Z → Z, n ↦ n + 3 ist .Beispiel: Funktion surjektiv? Bei der Funktion y = f(x) = x 2 kommt es darauf an, wie der Wertebereich definiert wird. In unserem zweiten Beispiel ist f(x) nicht surjektiv, da es Farben gibt, die nicht das Ergebnis .Oberbegriffe: [1] rechtstotal.