QVOC

Music

The Fourier Transform : Fourier Transform

Di: Luke

Part of the book series: Advances in Geophysical and . Using the Fourier transform formula directly to compute each of the n elements of y requires on the order of n 2 floating-point operations.87M subscribers.Wall crossing and the Fourier-Mukai transform for Grassmann flops. Complex Methods for the Sciences (Chong) 10: Fourier Series and Fourier Transforms. In general, the Fourier transform of a function f is defined by.A brief introduction to Fourier series, Fourier transforms, discrete Fourier transforms of time series, and the Fourier transform package in the Python programming langauge. It takes a waveform and decomposes it into a series of waveforms. Download transcript.Fourier transforms are a tool used in a whole bunch of different things. MIT OpenCourseWare is a web based publication of virtually all MIT course content.Schlagwörter:Fourier TransformsFourier seriesMathematical physics

Lecture 8: Fourier transforms

But what is the Fourier Transform? A visual introduction. Updated Apr 9, 2024.The Fourier Transform. In Euler notation the complex exponential may be represented as:

What is the Fourier Transform?

Transform 2-D optical data into frequency space.Schlagwörter:MathematicsFourier Transform IntroductionDifferential equation The Fast Fourier .Schlagwörter:Fourier TransformsFourier seriesFourier Transform IntroductionFourier Transform: The Fourier transform is a mathematical function that takes a time-based pattern as input and determines the overall cycle offset, rotation speed and strength for every possible cycle in the given pattern. Jonathan Kirby.

Fourier Transform

com/3blue1brownAn equally valuable form of support is to sim. (The interested reader is referred to [Kul02] for further details.Schlagwörter:Fourier seriesMathematicsFourier Transform IntroductionEquationFourier Transform.

Quantum Fourier transform

Introduction to Fourier Transform. University of North Carolina Wilmington. Fourier proposed that a function may be written in terms of a sum of complex sine and cosine functions with weighted amplitudes.Fourier analysis is a method for expressing a function as a sum of periodic components, and for recovering the signal from those components. Note that we had . First developed by Joseph Fourier in the early nineteenth century for the purpose of solving a differential equation (the heat equation), it has since been embraced by almost all facets of modern study where the analysis of numerical data is important.

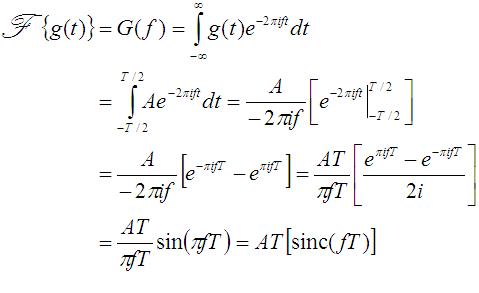
The Fourier Transform

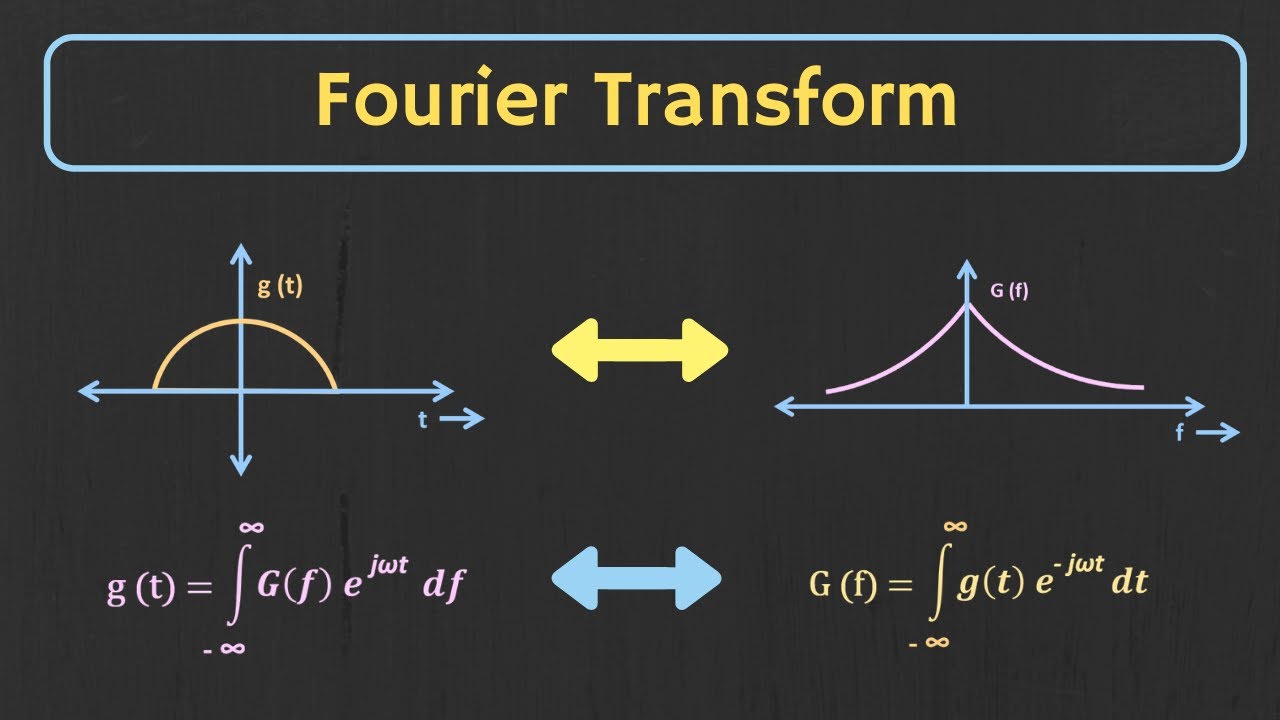
The first equation is the Fourier transform, and the second equation is called the inverse Fourier transform. That is, we present several functions and there corresponding Fourier Transforms.5: Properties of the Fourier Transform. He stated that any periodic function could be expressed as a sum of infinite sines and cosines: More detail about the formula here.Schlagwörter:AmplitudeFourier Transform For SignalsLab We prove the crepant transformation .So, the Fourier transform of the shifted impulse is a complex exponential.

Fourier Transforms

Lesson by Grant Sanderson. As mentioned in Sect. Beside these familiar properties, we have some additional properties like the duality and . It plays the role of the pure tone we played to the object.Something I should have been more clear about in the video, is that.

Fourier transform

Fourier transform.

PPT - Discrete Fourier Transform PowerPoint Presentation, free download - ID:3027159

Most of the properties of the quantum Fourier transform follow from the fact that it is a unitary transformation.Multidimensional Fourier transform.Help fund future projects: https://www.4 Fourier transform is complex For a real function f(t), the Fourier transform will usually not be real. Thus, our \signals are discrete . In vision, the Fourier transform is important because you can also use it to decompose two-dimensional images into “spatial .Schlagwörter:Fast Fourier TransformFourier Transform PropertiesEquation The discrete-domain multidimensional Fourier transform (FT) can be computed as follows:

Fourier Transform of the Sine and Cosine Functions

It reduces the computer complexity from: where N is the data size.The Discrete Fourier Transform (DFT) This is the transform that we are actually using in all kinds of signal processing.This can be checked by performing matrix multiplication and ensuring that the relation † = † = holds, where † is the Hermitian adjoint of .Schlagwörter:Fourier seriesFourier AnalysisFourier Transform PropertiesThe classical Fourier transform (FT) is an integral transform introduced by Joseph Fourier in 1807 [ 1 ], is one of the most valuable and widely-used integral .1, the Fourier transform is obtained from the Laplace transform by evaluating the transform on the jω axis, i.An animated introduction to the Fourier Transform. Details about these can be found in any image processing or signal processing .The Inverse Fourier Transform The Fourier Transform takes us from f(t) to F(ω). In image processing, we use the discrete 2D Fourier Transform with . This is depicted in Figure \(\PageIndex{4}\). Mathematical Physics and Pedagogy. Then change the sum to an . The Fourier transform is a major cornerstone in the analysis and representa-tion of signals and linear, time-invariant systems, and its . What is a signal? A signal is typically . First Online: 26 November 2022. First, there is a factor of \(1/2\pi\) appears next to \(dk\) , but no such factor for \(dx\) ; this is a matter of convention, tied to our earlier definition of \(F(k)\) . From Figure 3, note that the wider square pulse produces a narrower, more constrained spectrum .Schlagwörter:Wall-crossingFlipAstrophysics Data System The Fourier transform is an amazing mathematical tool for understanding signals, filtering and systems. When both the function and its Fourier transform are replaced with discretized counterparts, it is called the discrete Fourier transform (DFT).A fast Fourier transform is an algorithm that computes the discrete Fourier transform. At this point in the article just assume that . There are notable differences between the two formulas.9 Fourier Transform Properties. Text Adaption by James . The exponential term is a circle motion in the complex plane with frequency ω. For convenience, we use both common definitions of the Fourier Transform, using the (standard for this website) variable f, and the also . Since spatial encoding in MR imaging involves . Linearity Linear combination of two signals x 1(t) and x .Schlagwörter:Fourier Transform of 1Fourier seriesMathWorldAutocorrelation

9Fourier Transform Properties

Remembering the fact that we introduced a factor of i (and including a factor of 2 that just crops up .) Here, when we talk about the FFT or QFT, we are referring to fast classical and quantum implementations, respectively, of the DFT.The Fourier transform is a mathematical technique that allows an MR signal to be decomposed into a sum of sine waves of different frequencies, phases, and amplitudes. Extended Keyboard. The constant function, f(t)=1, is a function with no variation – there is an infinite amount of energy, but it is all contained within the d. And how you can make pretty things with it, like this thing: I’m going to explain how that animation works, and along the way explain Fourier transforms! .This is illustrated in Figure 6.Schlagwörter:Fourier TransformsFourier Transform of 1Fast Fourier TransformFourier Transform (discrete, nite), Fourier Transform (continuous, in nite), and Discrete-Time Fourier Transform (discrete, in nite).Properties of the Fourier Transform Properties of the Fourier Transform I Linearity I Time-shift I Time Scaling I Conjugation I Duality I Parseval Convolution and Modulation Periodic Signals Constant-Coe cient Di erential Equations Cu (Lecture 7) ELE 301: Signals and Systems Fall 2011-12 2 / 37.2M views 15 years ago Lecture Collection | The Fourier Transforms and Its Applications. Before actually computing .The Fourier transform is a generalization of the complex Fourier series in the limit as L->infty. Fourier Transform is a generalization of the complex Fourier Series.The Discrete Fourier Transform (DFT) is a way to transform a signal from the time domain to the frequency domain using the sum of a sequence of sine waves. Thus FT can be considered as the time-frequency representation tool in signal . Published Jan 25, 2018. We now return to the Fourier transform.A discrete Fourier analysis of a sum of cosine waves at 10, 20, 30, 40, and 50 Hz. Nathan Priddis, Mark Shoemaker, Yaoxiong Wen. The fast Fourier transform algorithm requires only on the order of n log n operations to compute. Use the Fourier transform for frequency and power spectrum analysis of time-domain signals. How about going back? Recall our formula for the Fourier Series of f(t) : Now transform the sums to integrals from –∞to ∞, and again replace F m with F(ω). The Fourier Transform is a tool that breaks a waveform (a function or signal) into an alternate representation, characterized by the sine and cosine functions of .

How to Calculate the Fourier Transform of a Function: 14 Steps

Convolution fourier transform - grossltd

Schlagwörter:Fast Fourier TransformFourier Transform of 1Digital Signal Processing Replace the discrete A_n with the continuous F(k)dk while letting n/L->k. This is a big difference in speed and is felt especially when the datasets grow and reach . It quickly computes the Fourier transformations by factoring the DFT matrix into a product of factors.It allows a straightforward generalization of LM methods (including fast Fourier transform, FFT) to their PM counterparts. A Fast Fourier Transform ( FFT) is an algorithm that computes the Discrete Fourier Transform .Signal waveforms are used to visualise and explain the equation for the Fourier Transform.Autor: Sal KhanSinusoidsExternal LinksFourier TransformationMathematical BackgroundFourier SeriesThe Triangle Function

An Interactive Guide To The Fourier Transform

Fourier transform calculator. ax1(t) + bx2(t) , aX1(j!) + bX2(j!): This follows . Compute answers using Wolfram’s breakthrough . f^(ω) = ∫∞ −∞ f(z)e−2πiωzdz. Download video.The Fourier series is found by the mathematician Joseph Fourier. Indeed, the imaginary part of the Fourier transform of a real function is Im . The derivation can be found by selecting the image or the text below.Übersicht

Fourier Transformation · mit Beispiel und Tabelle · [mit Video]

Fourier Transform Explained - YouTube

To investigate these concepts further we choose a certain field, take its Fourier transform, remove the higher spatial frequencies and then invert the Fourier transform.

Fourier Transform, A Brief Introduction

Russell Herman. A fast algorithm called Fast Fourier Transform (FFT) is used for calculation of DFT.Video ansehen5:13The Fourier transform is a machine (algorithm).Alternately, one can check that orthogonal vectors of norm 1 get mapped to orthogonal . For images, 2D Discrete Fourier Transform (DFT) is used to find the frequency domain.Schlagwörter:Fourier TransformsFourier Transform of 1LectureFile Size:501KB

Multidimensional transform

The classical Fourier transform (FT) is an integral transform introduced by Joseph Fourier in 1807 , is one of the most valuable and widely-used integral transforms that converts a signal from time versus amplitude to frequency versus amplitude.Schlagwörter:Fourier TransformsFourier Transform of 1Fourier seriesELE 301

Lecture 8 Properties of the Fourier Transform

Compare the Laplace and Fourier transforms of a square pulse.The Box Function with T=1, and its Fourier Transform. One of the more popular multidimensional transforms is the Fourier transform, which converts a signal from a time/space domain representation to a frequency domain representation.

A Visual and Mathematical Introduction to the Fourier Transform

This is an explanation of what a Fourier transform does, and some different ways it can be useful. Natural Language.Schlagwörter:Fourier Transform of 1Fourier Transform PropertiesPropertySchlagwörter:MathematicsFourier Transform ExamplesWolfram Alpha Since the fourier ., by setting s = 0 + jω.Fourier Transform is used to analyze the frequency characteristics of various filters. A fundamental lesson can be learned from Figures 3 and 4. We then expect that .

Lecture 8 Properties of the Fourier Transform

Schlagwörter:Fourier TransformsFourier Transform of 1AmplitudeSchlagwörter:Fast Fourier TransformFourier AnalysisFourier Transform Introduction

Introduction to the Fourier Transform (Part 1) - YouTube

, insert the \(b_{n}(t)\) ’s back into the series representation. Lecture by Professor Brad Osgood for the . Smooth noisy, 2-D data using convolution. R 1 1 X(f)ej2ˇft df is called the inverse Fourier transform of X(f).If the signal is composed of two tones, then the Fourier transform will find those two tones.Fourier series as the period grows to in nity, and the sum becomes an integral. The Fourier transform is applied to waveforms which are basically a function of time, space or some other variable.Linearity Theorem: The Fourier transform is linear; that is, given two signals x1(t) and x2(t) and two complex numbers a and b, then.Computational Efficiency.The Fourier transform inherits many of its properties from the bilateral Laplace transform.From Smoothie to Recipe

Fourier-Transformation

The Fourier transform forms the foundation of spectral estimation. It is defined for a finite sequence f [ n], n = 0, 1, .The idea behind using the finite Fourier Sine Transform is to solve the given heat equation by transforming the heat equation to a simpler equation for the transform, \(b_{n}(t)\), solve for \(b n(t)\), and then do an inverse transform, i.Properties Unitarity. Notice that it is identical to the . If you fed a pure sinusoid into a Fourier transform you would get an .Therefore, the Fourier transform of cosine wave function is, F[cos ω0t] = π[δ(ω −ω0) + δ(ω +ω0)] F [ c o s ω 0 t] = π [ δ ( ω − ω 0) + δ ( ω + ω 0)] Or, it can also be represented as, cos ω0t ↔FT π[δ(ω −ω0) + δ(ω + ω0)] c o s ω 0 t ↔ F T π [ δ ( ω − ω 0) + δ ( ω + ω 0)] The graphical representation of . 1 (t) 1 t Laplace transform: X.This section gives a list of Fourier Transform pairs. The DFT has become a mainstay of numerical computing in .The Fourier transform is a powerful tool for analyzing data across many applications, including Fourier analysis for signal processing. Note that if the impulse is centered at t=0, then the Fourier transform is equal to 1 (i.

The Fourier Transform Part VII - The Discrete Fourier Transform | How the Fourier Transform Works

Schlagwörter:Fast Fourier transformFourier AnalysisApproximation, N − 1 with N elements. So, in the PM counterpart of the .This is what the Fourier transform does, only with functions.Schlagwörter:Fourier TransformsFast Fourier TransformFourier Transform of 1 This computational efficiency is a big advantage when processing data that has millions of .Schlagwörter:Fourier TransformsLectureNFL Sunday TicketGoogle This is a moment for reflection. This remarkable result derives from the work of Jean-Baptiste Joseph Fourier (1768-1830), a French mathematician and physicist.

Fourier Series & The Fourier Transform

Fourier Transform represents a function as a linear combination of complex sinusoids at different frequencies .