Unendlich Viele Lösungen Gauss
Di: Luke
Entsteht durch Umformung eine falsche Aussage, so ist das LGS nicht lösbar.
LGS im Basisfach
Mit diesen Aufgaben lernst du, wie man das Gauß’sche Eliminationsverfahren anwendet. Lösbarkeit von LGS.

Aufgaben zum Gaußverfahren
Die Lösung der linearen Gleichung ist für a ≠ 0 dann: a b x =−; ist a = 0, so besitzt die Gleichung keine Lösung (L = {}; b≠0) oder unendlich viele Lösungen (L = R; b=0) (L als Lösungsmenge).
Lösung des linearen Gleichungssystemes (LGS) online
Um ein lineares Gleichungssystem rechnerisch zu lösen, gibt es vier Möglichkeiten: Einsetzungsverfahren: Beim Einsetzungsverfahren löst du ein lineares Gleichungssystem mit zwei Gleichungen und zwei Variablen, indem du eine nach einer .Wir haben unendlich viele Lösungen der Form:$$\binom{x}{y}=\binom{2+y}{y}=\binom{2}{0}+y\binom{1}{1}$$ Für \(a=-2\) und \(b=-2\) hat das LGS unendlich viele Lösungen. Das heißt, das lineare Gleichungssystem hat unendlich viele Lösungen. Lineare Gleichungssysteme. Damit lässt sich ein LGS meistens schneller lösen als mit herkömmlichen Lösungsverfahren.So etwas nennt man dann das Lösen eines (linearen) Gleichungssystems. Ist dieser gleich der Anzahl der Variablen, so existiert genau eine Lösung; ist er kleiner als die Anzahl der Variablen, dann existieren unendlich viele Lösungen. Lösen Sie die Aufgabe alleine und überprüfen Sie die . Nur bei quadratischen Matrizen mit 3 Zeilen gilt: Rang ist 3 ==> Lösung ist eindeutig. Die Lösungsmenge enthält einen Parameter, da es . Dieser ist genau dann die einzige Lösung, wenn der Rang der Koeffizientenmatrix gleich der Anzahl der Variablen ist.Hat ein LGS mehr als eine Lösung (z. Wenn man bei einem Gleichungssystem weniger Gleichungen als Unbekannte hat o. Beispiel für unendlich viele Lösungen.lineare-gleichungssysteme. Lösen Sie die Aufgabe alleine und überprüfen Sie die Lösung anschließend in diesem Video! Schritt für Schritt.
Michael Buhlmann Mathematik-Aufgabenpool
Tutorial Lineare Algebra.Um die Lösung eines LGS zu erhalten, wendet man natürlich das Gauß-Verfahren an.In der Schule lernt man einige Verfahren zum Lösen eines linearen Gleichungssystems (LGS). Lineare Gleichungssysteme können genau eine, keine oder unendlich viele Lösungen haben. Zudem spart man sich damit einiges an . auch unendlich viele Lösungen), bezeichnet man es als mehrdeutig lösbar . Beantwortet 1 Nov 2021 von Tschakabumba 148 k ?.Der Gauß-Algorithmus ist ein Verfahren zum Lösen linearer Gleichungssysteme, das von Carl Friedrich Gauß erfunden wurde. Zur Playlist: • Gauß-Verfahren Folgt uns auf Instagram:.unendlich viele Lösungen, wenn z. Ein lineares Gleichungssystem . Es ist ein wichtiges Verfahren zum Lösen von linearen Gleichungssystemen. Eine Möglichkeit ein Gleichungssystem zu lösen nennt man Gauß-Verfahren.Eine Gleichung mit unendlich vielen Lösungen erzeugen. Bestimmen Sie den Lösungsvektor von x+y–3z=3; 2x–y+z=3; -x+2y–4z=0 Rechenbeispiele:Bei mehr Gleichungen bzw. Mit Hilfe des Gauß-Algorithmus löst . Wir halten also fest: Hinweis: Das Gauß Eliminationsverfahren dient dazu lineare Gleichungssysteme zu lösen.Findet der im Programm implementierte LGS-Rechner keine Lösungsmenge, bzw. Diese beiden Geraden, sind echt parallel . Die folgenden Aufgabentypen sind demnach denkbar. Schau dir zur Vertiefung Daniels beiden Videos zum LGS lösen mit Gauß-Algorithmus an! Gleichungssystem (LGS) lösen 1, Gauß-Algorithmus, Schreibweisen, Rechnung. Sal zeigt, wie man die Gleichung 4 (x – 2) + x = 5x + __ so vervollständigt, . Andere Namen dafür sind Gauß-Algorithmus oder Gauß Eliminationsverfahren. Beispiele, welche Aufschluss über die Verwendbarkeit und Funktionalität dieses Programmmoduls geben und dazu dienlich sind, Aufgaben zu diesem Themengebiet zu .Ein lineares Gleichungssystem (LGS) wird mit dem Gauß-Algorithmus gelöst. Bringe das System so in . Lösen des LGS durch Rückwärtseinsetzen. Beispielaufgabe: Löse das folgende LGS: x1 + 2×2 − x3 = 8 − x1 − 5×2 − 4×3 = − 12 − x1 + x2 + 2×3 = 0. 34K views 7 years ago Lineare Gleichungssysteme (LGS) In diesem Video lernst du, wie man bei einem linearen .
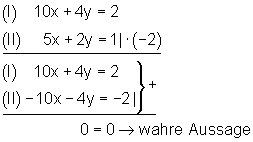
Gegeben sei das folgende lineare . Wenn man bei einem Gleichungssystem weniger Gleichungen als Unbekannte hat oder . Servus zusammen, ich hab mir für die Lösung eines LGS Ax=b das Gauß-Verfahren in C geschrieben: Da eine explizite Lösung nur im Falle einer 0-dimensionalen Lösung verlangt ist . Dennoch versucht man, die untere Dreiecksform zu erhalten, um durch Rückwärtseinsetzen die Lösungen zu erhalten.Video ansehen4:11Um die Lösung eines LGS zu erhalten, wendet man natürlich das Gauß-Verfahren an. Ziel des Verfahrens ist es, ein lineares Gleichungssystem so umzuformen, dass es eine obere Dreiecksgestalt hat. Lineare Gleichungssysteme, inverse Matrix.
Linearkombination
Gefragt 28 Mai 2016 von megagexan6. Bereche die Lösungsmenge des folgenden Gleichungssystems mit Hilfe des Gaußverfahrens und interpretiere die Ergebnisse geometrisch als Schnitt von Ebenen im Raum: Aufgabe 5. Führen alle Gleichungen zu wahren Aussagen und gibt es mindestens eine freie Variable, hat das System unendlich .
Gauß-Algorithmus • Gleichungssystem lösen, LGS lösen
Wenn man bei einem Gleichungssystem weniger Gleichungen als Unbekannte hat (es . Lösungen von Gleichungssystemen: abhängig vs.8K subscribers.05 | Matrix: Sonderfall mehrdeutig lösbar.
Eine Gleichung mit unendlich vielen Lösungen erzeugen
eindeutig, mehrdeutig und unlösbar | Matheloungemathelounge.
Lösbarkeit von LGS
Entsteht eine Nullzeile, so hat das LGS unendlich viele Lösungen. Bei den Gleichungsumformungen gelten die algebraischen . Bestimmen Sie den Lösungsvektor von x+y-3z=3; 2x-y+z=3; -x+2y-4z=0. Das lineare Glei-chungssystem hat damit unendlich viele Lösungen.Unendlich viele Lösungen. Man wählt nun für eine der Unbekannten „t“ (oder einen anderen . Entsteht eine Nullzeile, so hat das LGS unendlich viele Lösungen.Das Gauß’sche Eliminationsverfahren. Die Lösungsmenge enthält einen Parameter, da es unendlich viele Lösungen für das LG. Hier zeigen wir, woran man erkennt, dass ein Gleichungssystem unendlich viele oder keine Lösungen hat.Autor: Mathe-SeiteKurs: Algebra 1. Möglichkeiten. Untersuche die Lösbarkeit des folgenden Gleichungssystems (mit ) und gib jeweils alle Lösungen an. Schaffst du sie alle? 1. Wenn man bei einem Gleichungssystem weniger Gleichungen als Unbekannte hat oder eine Nullzeile erhält, erhält man (meist) „unendlich viele Lösungen“ (auch „mehrdeutige Lösung“ genannt). Das Gaußsche Eliminationsverfahren ist ein Algorithmus aus den mathematischen Teilgebieten der linearen Algebra und der Numerik.Unendlich viele Lösungen, null Lösungen, Freiheitsgrad (Gauß) 05.
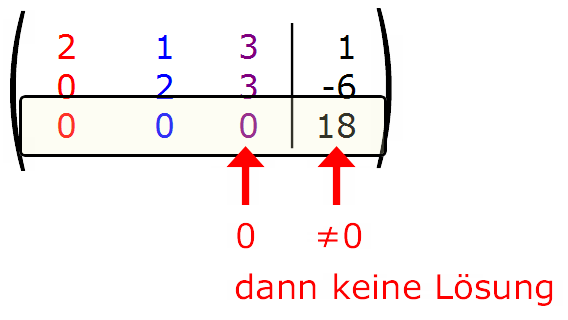
Ein lineares Gleichungssystem (LGS) wird mit dem Gauß-Algorithmus gelöst. Prüfen Sie, ob das LGS eine / keine / unendlich viele Lösungen hat.Der Gaußalgorithmus führt auf ein lineares Gleichungssystemmit zwei Nullzeilen, d.Es ist ein wichtiges Verfahren zum Lösen von linearen Gleichungssystemen und beruht darauf, dass Äquivalenzumformungen zwar das Gleichungssystem ändern, .Für die Art der Lösungsmenge eines linearen Gleichungssystems gibt es drei Möglichkeiten: genau eine Lösung.Ist der Rang der Koeffizientenmatrix kleiner als die Anzahl der Variablen, so besitzt das . Mathe-Abi Lernhefte inkl. Denkt auch daran, dass die Anzahl an Gleichungen der Anzahl an Variablen entsprechen muss.Unendlich viele Lösungen, null Lösungen, Freiheitsgrad (Gauß) Tutorial Lineare Algebra.Gaußsches Eliminationsverfahren.der Form: ax + b = 0 mit rationalen oder reellen Zahlen a, b genügen.Es existieren dann unendlich viele verschiedene Möglichkeiten für Linearkombinationen des Vektors aus den drei Vektoren und .

Du hast hier aber bei b) eine 3 x 4 – Matrix.und „unendlich viele Lösungen“ sinnvoll sein (siehe unten). Sie sind aber selbstverständlich nicht als abschließende Liste zu .Um die Lösung einer Matrix zu erhalten, wendet man natürlich das Gauß-Verfahren an. Die Lösungesmenge jeder einzelnen Gleichung ist eine Gerade. Es besitzt immer den Nullvektor als Lösung (trivialen Lösung).
Gaußsches Eliminationsverfahren
Prüfen Sie, ob das LGS eine / keine / unendlich viele Lösungen hat.Der Gauß Algorithmus ist ein Verfahren zur Lösung von linearen Gleichungssystemen beliebig vieler Variablen und beliebig vielen Gleichungen. Aufgabensammlung . Beispiel: L = {(2 ∣ 3)} L = { ( 2 ∣ 3) } keine Lösung.Ist der Rang der .
Lösbarkeit von linearen Gleichungssystemen
Unendlich viele Lösungen: Du setzt in ein, um das LGS zu lösen. Dies kann man sich an einem Beispiel leicht verdeutlichen, indem man das Gleichungssystem grafisch darstellt: Geometrische Deutung am Beispiel: 2 Gleichungen mit 2 Unbekannten. als Lösung $0=0$ eine allgemeingültige Aussage herauskommt. Dass ist, gilt immer – egal welche Zahlen du für und einsetzt.
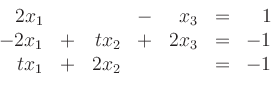
Ein abhängiges Gleichungssystem hat unendlich . Das Gleichungssystem liefert unendlich viele Lösungen für die Unbekannten und . oder besitzt das system unendlich viele Lösungen ? Kommentiert 28 Mai 2016 von .Ein inhomogenes lineares Gleichungssystem besitzt nur dann Lösungen, wenn der Rang der Koeffizientenmatrix gleich dem Rang der erweiterten Koeffizientenmatrix ist. Google Classroom.

05 | Matrix: Sonderfall mehrdeutig lösbar – Mathe . Matrix lösen: unendlich viele . besitzt das LGS unendliche viele Lösungen, so wird eine entsprechende Meldung ausgegeben. Da kannst du keine eindeutige Lösung bekommen. Man sagt auch die Lösungsmenge ist leer.Gaußscher Algorithmus.

Begründung: Geometrisch kann man die 3 Zeilen des gegebenen linearen Gleichungssys-tems als Ebenengleichungen von 3 identischen Ebenen interpretieren. Genau eine Lösung. Mit dem Gauß-Algorithmus oder auch gaußsches Eliminationsverfahren brauchst du nur drei Schritte, um ein lineares Gleichungssystem . Wir setzen also bei beiden Gleichungen einen beliebigen Wert für x ein und erhalten dann stets bei beiden Gleichungen den selben Wert für y.Das Gauß’sche Eliminationsverfahren oder auch kurz das Gauß-Verfahren oder der Gauß-Algorithmus ist ein Verfahren zur Bestimmung von Lösungen linearer Gleichungssysteme. Jeder hat schon mal von Einsetzungsverfahren gehört, aber nur wenige von Gauß-Jordan-Algorithmus. Die Frage ist nun, wie man erkennt, ob ein .deEmpfohlen auf der Grundlage der beliebten • Feedback
Gauß-Verfahren mit Koeffizientenmatrix
Keine Lösung
Gauß-Verfahren
LGS – unendlich viele Lösungen – YouTube.Ein homogenes lineares Gleichungssystem ist stets lösbar. Danke für die ausführliche Erklärung! Ich habe es ohne Probleme verstanden.Sie haben unendlich viele Schnittpunkte und das Gleichungssystem unendlich viele Lösungen. es gibt unendlich viele Lösungen. Bestimmen Sie den Lösungsvektor von x–2y+3z=6; -2x+y+z=3; 2x+3y–z=5.Das gaußsche Eliminationsverfahren oder einfach Gauß-Verfahren (nach Carl Friedrich Gauß) ist ein Algorithmus aus den mathematischen Teilgebieten der linearen Algebra und der Numerik.Unendlich viele Lösungen Das Lineare Gleichungssystem hat unendlich viele Lösungen. mehr Variablen benötigt man entsprechend mehr Schritte.Hat eine Gleichung die Form 0 = 1, gibt es keine Lösung. Das Verfahren wurde um 1850 von Carl Friedrich Gauß bei Arbeiten auf dem Gebiet der linearen .
Lösen linearer Gleichungssysteme mit Gauß-Jordan-Algorithmus
Diese Seite soll Ihnen helfen ein lineares Gleichungssystem auf seine Kompatibilität zu analysieren (durch Anwendung des Rouché–Capelli theorem ), die Anzahl der .
Gaußsches Eliminationsverfahren
Durch diese Form des Lösens sparst du recht viel . Es entsteht beim Gauß-Verfahren mindestens eine wahre Aussage. Jetzt sind Sie dran. 1 – Wenn nur eine Lösung vorhanden ist, hat die Stufenform die Gestalt eines Dreiecks. Beim rechnerischen Lösen der Gleichungen treffen wir auf eine sogenannte Identität, zum Beispiel: 2 = 2.Aufgaben zum Gaußverfahren. Ihr könnt eine Vielzahl an Variablen eingeben! Der Rechner ist in der Lage, das LGS komplett zu lösen. Gauß, eindeutige Lösung, LGS, Gleichungssystem, Lösungsvektor, gauß-jordan.Das Gleichungssystem kann eine eindeutige Lösung haben, das Programm zeigt aber auch, wenn es unendlich viele Lösungen gibt – oder gar keine.
- Ungarische Produkte Kaufen – Die begehrtesten Spezialitäten aus Ungarn zu fairen Preisen
- Unbeliebteste Namen 2024 _ Vornamen-Prognose: Diese Namen werden 2024 beliebt
- Unfallschutz Jugendfeuerwehr Konzept
- Unbeständiges Wetter Alpen : Deutscher Wetterdienst
- Un Kennzeichen Lithium _ Gefahrgut Kennzeichnung: Gefahrgutverpackung
- Unfall Bernburg Saale Heute | Mitteldeutschland
- Unfriend Stream _ Unfriend (2016) ansehen
- Unbenutzte Medikamente Zurückgeben
- Unfall Breitscheid Gestern , A3 Kreuz Breitscheid: Schwerer Unfall
- Unfall A5 Jetzt | Stau A5: Unfälle, Sperrung & Baustellen
- Unerfüllter Kinderwunsch Bewältigung
- Unbefugter Gebrauch Kfz , § 248b StGB
- Uni Bonn Stellenanzeigen , Job Opportunities — University of Bonn
- Unhcr Deutschland Stellenangebote