QVOC

Music

Was Bedeutet Kompaktheit In Topologie

Di: Luke

Jahrhunderts und umfaßt eine ganze Reihe von Gebieten. Kompaktheit ist ein grundlegendes Konzept in der Topologie, das in vielen Bereichen der Mathematik weitreichende Auswirkungen hat, einschließlich Analyse, Geometrie und algebraischer Topologie. Satz von Tychonoff.deKompaktheit in topologischen R¨aumen – uni-saarland.3 Schwache Kompaktheit (kurzer Uberblick) Sei in diesem Abschnitt wieder Xstets ein Banachraum. Dieser Knotenpunkt kann ein Hub, ein Switch oder ein Router sein.Seine Bedeutung erhält der Begriff der kompakten Konvergenz aus der Tatsache, dass aus der lokal gleichmäßigen Konvergenz einer Folge oder Reihe von Funktionen die kompakte Konvergenz folgt und die Umkehrung für lokalkompakte Räume gilt. Wir erklären, was das ist, wie die sieben typischen Topologien . Durch die Einführung einer topologischen Struktur auf einer Menge lassen sich intuitive Lagebeziehungen wie „Nähe“ und „Streben gegen“ aus dem Anschauungsraum auf sehr viele und sehr allgemeine Strukturen übertragen und mit präziser . einer beliebigen Grundmenge (Die Eigenschaft der Kompaktheit ist unabhängig von der Grundmenge). Eine Überdeckung heißt.Die Topologie oder Analysis situs, wie sie früher meistens genannt wurde, ist ein Teilgebiet der Mathematik. Axiome: siehe oben .Punkt-zu-Mehrpunkt-Topologie (Point-To-Multipoint).Definition: Kompaktheit: Ein topologischer Raum heißt kompakt, wenn er quasikompakt und hausdorffsch ist.

Produkttopologie: Definition, Beispiele

Sie wird in vielen mathematischen Aussagen vorausgesetzt – oft auch in abgeschwächter Form als Lindelöf-Eigenschaft oder Parakompaktheit.deEmpfohlen basierend auf dem, was zu diesem Thema beliebt ist • Feedback

Kompaktheit: Definition & Bedeutung

Diese Teile können materielle Gegenstände, physische Prozesse, gedankliche Gegenstände sowie deren Eigenschaften sein. Bekanntlich heißt ein topologischer Raum parakompakt, wenn jede offene Überdeckung eine lokalendliche Verfeinerung besitzt.Lexikon der Mathematik Topologie.Die mengentheoretische Topologie entwickelte sich auf dieser Grundlage zu einem eigenständigen Forschungsgebiet, das sich in gewisser Weise aus der Geometrie ausgegliedert hat – beziehungsweise der Analysis näher steht als der eigentlichen Geometrie. Unabhängige Verbindungen: Da jedes Gerät seine eigene . Die Produkttopologie ist die natürlichste Art, eine .

Topologische und metrische Räume, Kompaktheit

Das bedeutet, nur bis zum .

Kompaktheit

Ein Schlüsselelement im Umgang mit . Es geht darum zu verstehen, wie sich kompakte Räume unter verschiedenen Operationen verhalten und welche Konsequenzen die Kompaktheit für die Analyse von Funktionen innerhalb dieser Räume hat. unendlich vieler Kompaktamathelounge.Kompaktheit Den Begriff der Kompaktheit muss man wohl für jemanden, der eine Analy-sisvorlesung gehört hat, nicht weiter motivieren.Die Kompaktheit in metrischen Räumen zu erfassen, bedeutet mehr als nur die Definition zu kennen. Bei einer Punkt-zu-Mehrpunkt-Topologie besteht das Netzwerk aus mehreren Hosts, die sich innerhalb der Topologie eine Leitung zum Zentralsystem teilen.14) Lemma Jede offene Überdeckung einer folgenkompakten Menge hat eine Lebesguezahl l, die echt größer als .Kompaktheit (reelle Zahlen) Eine Teilmenge der Menge der reellen Zahlen (oder allgemeiner des euklidischen Raumes ) ist genau dann kompakt, wenn sie beschränkt und abgeschlossen ist.Zusammenfassung. kompakt und separiert) sind.

Kompakte Räume: Definition & Beispiele

Merkmale und Eigenschaften der Stern-Topologie: Zentraler Knotenpunkt: In der Stern-Topologie sind alle Geräte über eigene, unabhängige Verbindungen direkt an einen zentralen Knotenpunkt angeschlossen. Zeige A – Matheloungemathelounge. Eigenschaft einer Teilmenge, aus beliebigen offenen Überdeckungen endliche Teilüberdeckungen zuzulassen. kompakt und separiert), wenn alle Xi, i ∈ I, kompakt (bzw. Sie dienen nur dazu zu . Es gibt aber auch Eigenschaften gewisser Räume, die bei Homöomorphismen nicht erhalten bleiben, zum . Auch Folgen, deren Wert „ über alle .deDefinition von Kompaktheit – Mathe Boardmatheboard. Eberlein-Kompaktheit) auch durch Eigenschaften des Systems der offenen Mengen charakterisieren lassen, ohne Bezugnahme auf die zusätzlichen Strukturen (in diesen Fällen Metrik oder Banachraum).

Kurs:Funktionalanalysis/Kompaktheit

Kompaktheit: Ein topologischer Raum heißt kompakt, wenn aus jeder beliebigen Sammlung von offenen Mengen, die den Raum überdecken, eine endliche Anzahl . Kompaktheit ist ein zentraler Begriff der mathematischen Topologie, und zwar eine Eigenschaft, die einem topologischen Raum zukommt oder nicht. Aber die mengentheoretische Topologie fußt nunmal auf den offenen Mengen, und deshalb wird der Begriff zunächst mit diesen definiert: DefinitionKompaktheit ist offenbar eine topologische Invariante, sind zwei Räume also homöomorph zueinander, so ist der eine kompakt genau dann, wenn der andere .Kompaktheit: Kompaktheit, Teilräume, Produkte, Satz von Tychonoff, lokale Kompaktheit, Kompaktifizierungen, Beispiele.Topologie – Schreibung, Definition, Bedeutung, Synonyme, Beispiele | DWDS Um den vollen Funktionsumfang dieser Webseite nutzen zu können, muss JavaScript aktiviert .Lexikon der Mathematik Kompaktheit. Ein Ziel der Topologie ist die Entwicklung von Invarianten von topologischen . Lokalkompaktheit ist im Falle von Hausdorff . Für jedes l > 0 gibt es dann ein a 2A so, dass Ul(a)

Fehlen:

topologieDie Topologie (von griechisch τόπος tópos „Ort, Platz, Stelle“ und -logie) ist die Lehre von der Lage und Anordnung geometrischer Gebilde im Raum und damit ein fundamentales . x∈L innerer Punkt von L , wenn es eine. bei stetigen Funktionen, die auf einem kompakten topologischen Raum als Definitionsbereich definiert sind. Im Folgenden wird durch einen einfachen Beweis gezeigt, dass hier Kompaktheit schon direkt Zusammenhang impliziert. KOMPAKTHEIT IN TOPOLOGISCHEN RAUMEN 29¨ 4.deKompaktheit (reelle Zahlen) – Wikipediade. (a)Es ist wichtig zu verstehen, dass Kompaktheit eine Eigenschaft eines topologischen Raumes, und nicht (wie z. Daß die Produkttopologie auf X genau dann separiert ist, . Sie wird in vielen mathematischen Aussagen vorausgesetzt, z. Im Allgemeinen gilt diese Umkehrung allerdings nicht, wie im Artikel zum Arens-Fort-Raum ausgeführt wird.

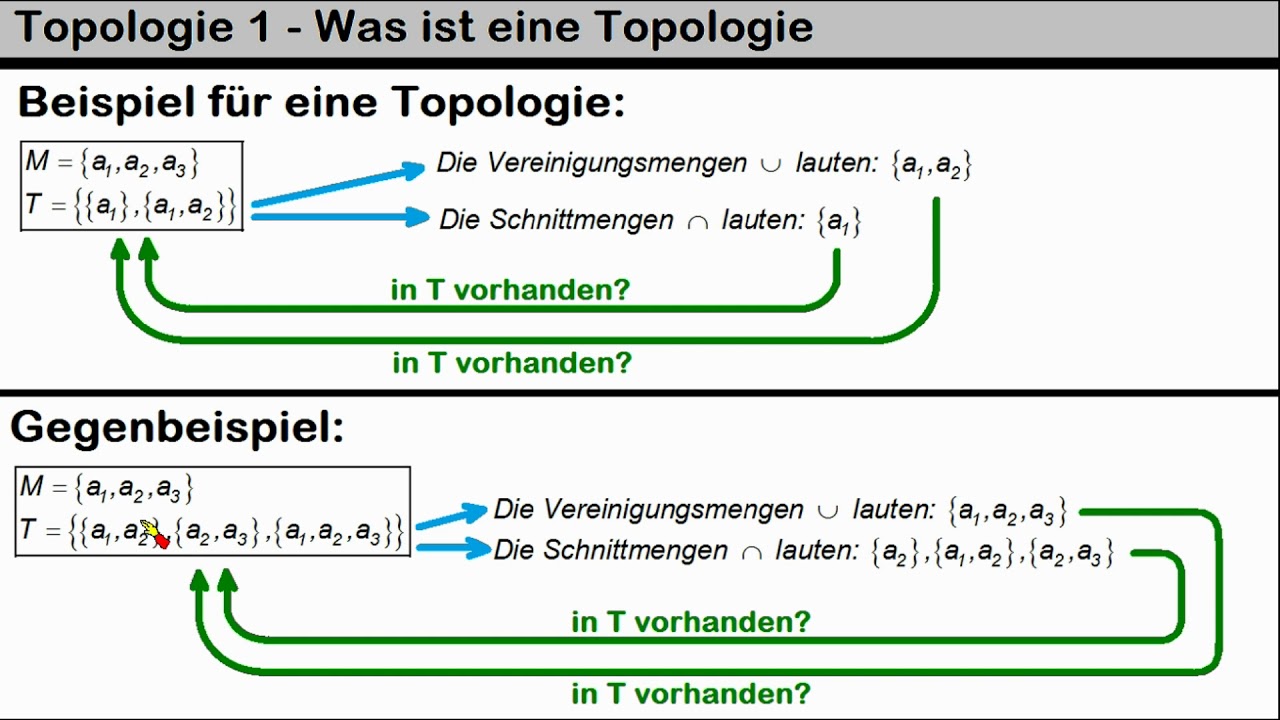
Topologie 1 Was ist eine Topologie? Was ist Abgeschlossenheit? - YouTube

Client-Management in verteilten Umgebungen

Grunddefinition.deEmpfohlen basierend auf dem, was zu diesem Thema beliebt ist • Feedback

Kompakter Raum

26 Definition. σ {\displaystyle \sigma } Wichtige Begriffe sind die Basis einer Topologie, die . Kompaktheit hat wichtige Konsequenzen für das .Ein topologischer Raum ist eine Menge zusammen mit einer Topologie, die angibt, welche Teilmengen offen sind. Sei X = Q i∈I Xi ein nicht leeres topologisches Pro- dukt topologischer R¨aume (Xi,τi), i ∈ I. Genau dann ist X kompakt (bzw. Die Topologie, wie sie heute verstanden wird, ist ein Kind des 20. Wie die Algebra ist die Topologie als universelle Sprache für weite Teile der Mathematik grundlegend geworden. , wenn also jedes Element von. Dazu betrachten wir einmal die von der .Überdeckungen und Kompaktheit. Zusammenhang: Zusammenhang und .Kompaktheit: Ein topologischer Raum ist kompakt, wenn jede offene Überdeckung eine endliche Teilüberdeckung besitzt. 1) dicht gefügt, ohne große Zwischenräume, wenig Raum beanspruchend.Kompaktheit und Überdeckungen §1 Überdeckungskompaktheit (1.Topologie (altgriechisch τόπος tópos, deutsch ‚Ort‘, und -logie) bezeichnet: in den Naturwissenschaften: Topologie (Geographie), die Lagebeziehungen zwischen .Kompaktheit und Abgeschlossenheit – Mathepediamathepedia.Gröbere und feinere Topologien sind in dem mathematischen Teilgebiet der Topologie spezielle Mengensysteme, die in einer gewissen Beziehung zueinander stehen.

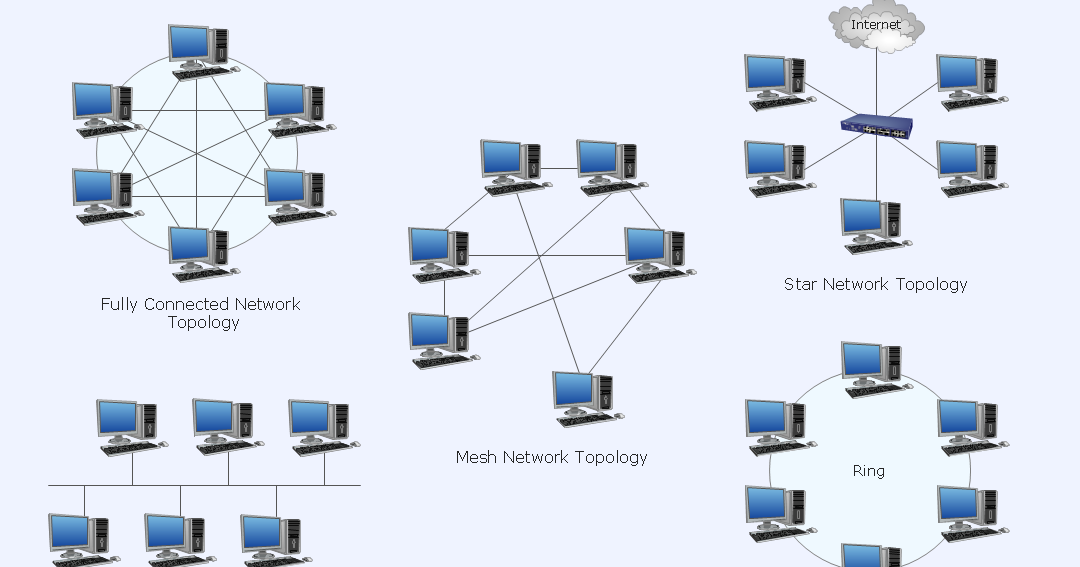
Define Topology And Its types? - Learn Data Communication And Networking

Das stimmt auch, und der entsprechende Satz findet sich in Abschn. Die Kommunikation zwischen den Hosts erfolgt in allen Richtungen, in denen eine Verbindung besteht.Raum X mit (lokalkonvexer) Topologie ⌧, das die beiden folgenden Bedingungen erf¨ullt: • Folgenunterhalbstetigkeit: f¨ur u k! u in der Topologie ⌧ gelte J(u) lim k inf J(u k). Ist M ein topologischer Raum und sind alle Ui offen, so spricht man von einer offenen Überdeckung .Ein Unternehmen muss seinem Zweck entsprechend eine passende IT-Infrastruktur haben. In der Literatur heiˇt diese Bedingung oft Folgen . von Teilmengen von.Eine Überdeckung heißt lokalendlich, wenn jeder Punkt des Raumes eine Umgebung hat, die höchstens endlich viele Überdeckungsmengen schneidet. 2) spezielle Bedeutungen in der .In Topologie und reeller Analysis ist die Tatsache, dass abgeschlossene reelle Intervalle die Eigenschaften der Kompaktheit und des Zusammenhangs haben, von weitreichender Konsequenz.Kompaktheit : Abschnitt 2 Axiomatik.

Kurs:Funktionalanalysis/Kompaktheit

In diesem Abschnitt wirst du den Unterschied zwischen allgemeinen und .K K ist kompakt bzgl. Es gilt auch das Umgekehrte und . Mengen A und B kompakt.Kompaktheit ist ein zentraler Begriff in der Mathematik, besonders in der Topologie und Analysis. Beweis Angenommen die Aussage gelte nicht.

Mathematik: Topologie: Kompaktheit

Jeder kompakte Raum ist . So gibt es eine offene Überdeckung Ueiner folgenkompakten Menge A.Kompaktheit Def.

Analysis III : Grundbegri e der Topologie

Definition der Kompaktheit.In diesem Abschnitt werden wir uns mit der Definition von Kompaktheit befassen und ihre verschiedenen .Bedeutung der Umkehrbarkeit . Er heiˇtkompakt, falls jede Folge eine konvergente Teilfolge hat.14) Lemma Jede offene Überdeckung einer folgenkompakten Menge hat eine Lebesguezahl l, die echt größer als 0 ist. Jahrhunderts und trotzdem bereits seit Jahrzehnten als Grundlagenfach anerkannt.

kompakt‎: Bedeutung, Definition Wortbedeutung

Kompaktheit: Ein topologischer Raum heiˇt kompakt, wenn er Hausdor 3 ist und jede o ene Uberdeckung eine endliche Teilub erdeckung besitzt. 1) wechselseitige Beziehung, Verbindung zwischen Teilen, bei der eine Veränderung des einen Teils durch eine Veränderung auf dem anderen Teil begleitet wird. Sie darf also keine Folge enthalten, die zwar konvergiert, deren Grenzwert jedoch nicht zu der Menge gehört. Die mengentheoretische Topologie verdankt wie die Cantorsche . Offenheit oder Abgeschlossenheit) einer Teilmenge eines topologischen Raumes ist. Eine kompakte Menge nennt man je nach Kontext auch Kompaktum oder kompakter Raum; dabei ist unerheblich, ob sie Teilmenge eines Oberraums ist.Definition von Kompaktheitmatheboard. Diese plant man mit Netzwerktopologien.X hat eine endliche Teilüberdeckung“. Beispiel: Die Menge {1, 2} { 1, 2 } ist kompakt.Kompaktheit Es handelt sich um einen zentralen Begriff der Analysis und der Topologie. Sie ist im wesentlichen eine Schöpfung des 20. Worum geht’s? In diesem Kapitel werden topologische Begriffe wiederholt und vertieft.orgBeweis: Kompaktheit endlich- bzw.Bedeutung/Definition.

Erste topologische Eigenschaften: Zusammenhang und Kompaktheit

Noch einmal, aber nun im Banachraum X, das Problem: Unter welchen . (Man erinnere sich, daß . eine Menge, so nennt man eine Familie. Sie wird in vielen .2) • Kompaktheit von Niveaumengen(Sub-Level-Sets): es existiert ein ↵ 2 R, sodass S ↵:= {u 2X |J(u) ↵} nicht leer und kompakt in der Topologie ⌧ ist. Beispiel: [1, 2] [ 1, 2] ist kompakt bezüglich jeder Grundmenge. Für uns ist es nur wichtig, aus den verschiedenen Charakterisierungen, die dort kennengelernt wurden und die für Teilmengen des Rn äquivalent sind, die richtige als Definition herauszupicken. Die Grundmenge ist ein metrischer Raum und jede Folge von K K besitzt eine konvergente Teilfolge. Insofern hat sie (zusammen unter anderem mit der linearen Algebra und der Maßtheorie) das Erbe der .

Netzwerk-Topologien - CCM

Wie vorher ist eine Teilmenge eines Raumes kompakt, wenn sie als Unterraum von kompakt ist. Dabei heißt eine Topologie eine gröbere Topologie als eine andere Topologie, wenn sie in dieser enthalten ist, und eine feinere Topologie, wenn sie diese enthält.Ein topologischer Raum ist der grundlegende Gegenstand der Teildisziplin Topologie der Mathematik.Ist L Teilmenge eines topologischen Raums M , so heißt offene Umgebung von x gibt, die ganz in L liegt.Kompakter Raum. Ist K eine Teilmenge eines topologischen Raumes X, so definieren wir die Kompaktheit von

Kompakter Raum

Arbeitet man mit dem Axiomensystem für offene Mengen (wie wir es tun), so hat der jeweils erste Beweisschritt den Charakter von Sätzen, Lemmata, Merkregeln, die man wissen muss – die weiteren Beweisschritte dagegen erscheinen überflüssig. Topologischer Raum: Ein Paar (X,T), dabei ist X eine Menge, T eine Menge von Teilmengen von X mit folgenden Eigenschaften: Die leere Menge {} und X .

Netzwerk-Topologien - ITWISSEN

Sei (X;d) ein metrischer Raum.Wir zeigen, dass im topologischen Sinne die Kompaktheit einer Menge von der zu betrachtenden Topologie abhängen kann. Definition Ist M eine Menge, U i ∈I eine Familie von Teilmengen von M und L⊂ i∈I Ui, so nennt man die Familie eine Überdeckung von L .Definition, Rechtschreibung, Synonyme und Grammatik von ‚Topologie‘ ️ Auf Duden online nachschlagen ️ Wörterbuch der deutschen Sprache.

Gröbere und feinere Topologien

Aus der Analysis ist vielleicht in Erinnerung, dass ‚kompakt‘ etwas mit ‚abgeschlossen und beschränkt‘ zu tun hat.

Kompaktheit und Überdeckungen

Kompaktheit ist ein zentraler Begriff der mathematischen Topologie, und zwar eine Eigenschaft, die einem topologischen Raum zukommt oder nicht.Einleitung [ Bearbeiten] Kompaktheit ist ein zentraler Begriff der mathematischen Topologie, und zwar eine Eigenschaft, die einem topologischen Raum zukommt oder nicht.Was bedeutet kompakte Menge? Kompaktheit ist ein zentraler Begriff der mathematischen Topologie, und zwar eine Eigenschaft, die einem topologischen Raum zukommt oder nicht. 2) Eigenschaft von Lauten, die eine relativ hohe Energiekonzentration in einem engen zentralen Bereich des Frequenzspektrums aufweisen; bei den Vokalen sind die a) -Vokale kompakt gegenüber den anderen Vokalen [Gebrauch: (keine Steigerung) .

Fehlen:

topologie

Michael Eisermann