Was Ist Das Geschwindigkeits-Zeit-Gesetz Für Harmonische Schwingung?
Di: Luke
Drehzahl Eines Motors
Bewegungsgesetze der Harmonischen Schwingung
Die Geschwindigkeit ist die zeitliche Änderungsrate des Ortes, also muss man nach der Zeit ableiten.Mechanik: Dynamik. Die Zeit, nach der ein Körper eine dieser periodischen Bewegungen genau einmal ausgeführt hat, nennt man die Periodendauer T.Eine Schwingung ist in der Physik definiert als jede Art von Bewegung, unabhängig von ihrer Regelmäßigkeit oder Rückkehr zum Ruhemittelpunkt. mit dem Impuls zusammen: Ekin = 1 2mv2 = p2 2m E k i n = 1 2 m v 2 = p 2 2 m. dige Schwingung braucht. Startet die Bewegung im stillen Zustand und vom Anfangspunkt aus, ist die Formel einfacher . nach gleichlangen Zeitabschnitten immer wieder den gleichen Bewegungszustand, d. Bewegungen: Grundlagen.
Geschwindigkeit-Zeit-Diagramm • einfach erklärt · [mit Video]

Zeit-Geschwindigkeit-Gesetz der gleichmäßig beschleunigten Bewegung – Formelumstellung. Nach einem Anstoß von außen schwingt ein harmonischer Oszillator . Sie entsteht durch eine Umwandlung von Schwingungsenergie .
Schwingungen Physik: Mechanik & Formeln
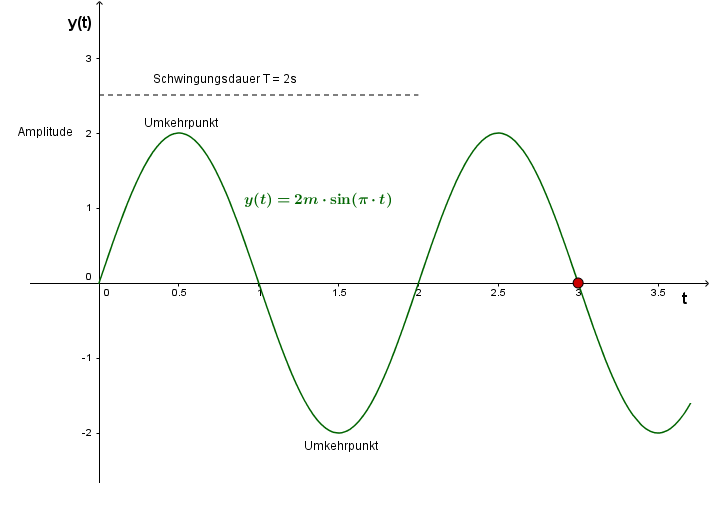
Ein harmonischer Oszillator ist ein schwingungsfähiges System, das sich durch eine lineare Rückstellgröße auszeichnet.Das Geschwindigkeits-Zeit-Gesetz der harmonischen Schwingung Die folgende Darstellung leitet die harmonische Schwingung aus einer Kreisbewegung her. Schwierigkeitsgrad: leichte Aufgabe.
Bedingung für harmonische Schwingungen
Amplitude Die Amplitude \( s_0 \) beschreibt die maximale Auslenkung einer Schwingung. Der Anstieg des Graphen im Diagramm entspricht dabei seiner Beschleunigung a an der jeweiligen Stelle. Diese Schwingungen sind in der Regel nicht endlos, weil das System meistens gedämpft wird. Zeit-Geschwindigkeit-Gesetz: v ( t) = ω ⋅ y ^ ⋅ cos.) weiter mit Geschwindigkeit und Beschleunigung eines harmonischen Oszillators. bei der Luftreibung oder auch der . Sie erinnert an die Winkelgeschwindigkeit einer kreisförmigen Bewegung, denn multipliziert mit der Zeit .Geschwindigkeit – Zeit – Gesetz einer harmonischen Schwingung . Um Aufgaben zum . Mit Sinus haben wir jetzt fast schon zu viel verraten.In Worten ausgedrückt sagt die obige Differentialgleichung: „Die zweite Ableitung der Ortsfunktion nach der Zeit ergibt wieder die Ortsfunktion mal einer negativen .deEmpfohlen auf der Grundlage der beliebten • Feedback
Geschwindigkeit und Beschleunigung eines harmonischen Oszillators
1 Der lineare . Des Weiteren rechnen wir ein Beispiel, lösen die allgemeine Differentialgleichung für Schwingungen und gehen auf die wirkenden Energien bei dem Federpendel ein. ist die Potentialkraft, die Gewichtskraft.Wenn du die Länge l des Fadens, die Masse m des Pendelkörpers, den Ortsfaktor g und die Amplitude x gegeben hast, kannst du die rücktreibende Kraft berechnen.

Dabei gehen wir davon aus, dass die . Welche der beiden Funktionen man am besten benutzt hängt von der Anfangssituation der Schwingung ab: Hat die Schwingung zur Zeit \(t = 0\) die Auslenkung (Elongation) \(y(0)=0\), benutzt man wegen \(\sin(0)=0\) besser die . 1 Verschiedene Varianten von gleichmäßig beschleunigten und verzögerten Bewegungen in Form von Zeit-Ort-, Zeit-Geschwindigkeit- und Zeit-Beschleunigung-Diagrammen Herleitung einer weiteren Bewegungsgleichung für die gleichmäßig beschleunigte Bewegung ohne Anfangsgeschwindigkeit Bewegungsgleichungen.
Bewegungsgleichungen
Eine Schwingung kann man genauer beschreiben, wenn man den zeitlichen Verlauf der Auslenkung y darstellt. In Abbildung 11.Die Schwingungsdauer T ist die Zeit, die man für eine vollstän.Wie ändert sich Die Geschwindigkeit Mit Der Zeit?
Harmonische Schwingung: Definition & Formel
Zieht euch doch einfach diesen heißen Streifen Physik rein und seht, was der Sinus damit zu tun hat. (01:25) Geschwindigkeit-Zeit-Gesetz. Die restlichen Energieformen wie Spann- und Lageenergie ergänzen die Bewegungsenergie immer zu einer konstanten Summe. Am ein-fachsten kann man die Schwingungsdauer messen, indem manDabei gibt die so genannte „Oszillator-Frequenz“ an. Diese Dämpfung ist in . Eine vollständige Schwingung liegt vor, wenn sich der Bewegungsablauf wiederholt, d. Die Schwingungsgleichung lautet nun: s(t) = s0 ⋅ sin(ωt +ϕ0 . Gesetz einer harmonischen Schwingung: Beschleunigung – Zeit – Gesetz einer harmonischen Schwingung: Schwingungsdauer T : eines Fadenpendels : eines Federschwingers : eines Torsionspendel : eines physischen Pendels : einer Flüssigkeitssäule: Kraftgesetze für .In der Formel stehen die Symbole A, ω, t und φ für Anfangsgeschwindigkeit, Zeit, Kraft und Masse.Bewegungsgleichung für eine ungedämpfte harmonische Schwingung: 0 2 2 ku dt d u m Elongation u eines Schwingers zum Zeitpunkt t ist gleich zum Phasenwinkel M Z 0 t M 0 Weg-Zeit-Gesetz der harmonischen Schwingung: u t u 0 nM u 0 n Z 0t M 0 u 0 –Amplitude bzw. Zeit-Ort-Gesetz: y ( t) = y ^ ⋅ sin. Es ist eine periodische Bewegung. Dabei muss man die Kettenregel beachten.; Periodendauer (Schwingungsdauer) Die Periodendauer ist die Zeit, die verstreicht, während ein schwingungsfähiges System genau eine Schwingungsperiode durchläuft, d.In diesem Video wird das Geschwindigkeits-Zeit-Gesetz (V-t-Gesetz) und das Beschleunigungs-Zeit-Gesetz (a-t-Gesetz) der der harmonischen Schwingung erklärt.Die Ort-Zeit-Gesetze einer Komponente der Kreisbewegung mit konstanter Geschwindigkeit und der harmonischen Schwingung stimmen überein.Ob eine Schwingung harmonisch ist, also die Weg-Zeit-Funktion eine Sinusfunktion ist, hängt davon ab, ob folgende Bedingung erfüllt ist: Bei einer harmonischen . Dies ist eine interaktive Aufgabe zu: Freie, harmonische Schwingungen mit praktischen Tipps zum Lösen und einer Zusammenfassung der nötigen Theorie. Mit N = k g ⋅ m s 2 ergibt sich: 15 k g ⋅ m s 2 = k ⋅ 0, 15 m. Bei einer harmonischen mechanischen Schwingung ist die rücktreibende Kraft proportional zur Auslenkung. Durch das Minuszeichen wird . nach der es sich wieder im selben Schwingungszustand befindet.Hierzu betrachten wir das Ort-Zeit-Gesetz, das Geschwindigkeits-Zeit-Gesetz sowie das Beschleunigungs-Zeit-Gesetz für ungedämpfte harmonische Schwingungen. Aus dem Zeit-Ort-Gesetz y ( t) = y ^ ⋅ sin.Harmonische SchwingungenMechanische SchwingungenDieses Thema eignet sich besonders, Phänomene aus verschiedenen Teilgebieten der Physik (hier beispielhaft für Mechanik und Elektrizitätslehre) mit einheitlichen mathematischen Mitteln zu beschreiben. Darüber kommen auch die Größen ω und φ, die zur Beschreibung einer Kreisbewegung mit konstanter Geschwindigkeit dienen. Man erhält dann ein y-t-Diagramm dieser Schwingung (Bild 2).Eine ausführlichere Herleitung der Schwingungsgleichung für gedämpfte Schwingungen kannst Du hier herunterladen! * Die geschwindigkeitsabhängige Dämpfung ist die häufigste Form der Dämpfung. (00:12) In einem Geschwindigkeit-Zeit-Diagramm, oder auch v – t -Diagramm, kannst du ablesen, wie schnell sich ein Körper zu einem bestimmten Zeitpunkt t bewegt. Um Aufgaben zum Zeit-Geschwindigkeit-Gesetz der gleichmäßig beschleunigten Bewegung zu lösen musst du häufig die Gleichung v = a ⋅ t nach einer Größe auflösen, die unbekannt ist. Auflösen nach k ergibt: k = 100 k g s 2.eine durch einen harmonische Funktion der Art \begin{equation}y(t)=a\cos(\omega t+\phi_{0})\end{equation} beschreibbare Bewegung. In unserem Video dazu, erklären wir dir das alles in wenigen Minuten.Bei harmonischen Schwingungen folgt aus dem linearen Kraftgesetz F = − k ⋅ y für die Energie E A u s stets E A u s = − 1 2 ⋅ k ⋅ y 2.
Mathematische Beschreibung harmonischer Schwingungen
Wir können als nächstes die Schwingungsdauer T bestimmen durch die Formel (siehe Schwingungsgleichung: Federpendel ): T = 2 π m k. Dabei wechselt das System immer zwischen zwei extremen . Schwingungsweite gehörigen Ordinatenwert 6. [math]v(t)=\dot s (t) = \dot{\hat y \sin(\omega t)} = \hat y \cos(\omega t) . Es gilt stets: F → ∼ − y →. s steht für die angebene Strecke in Meter und a ist für die Beschleunigung in Meter pro Sekunde-Quadrat und t ist die Zeit in Sekunden, sowie s0 steht für den Anfangsweg. (Zumindest bei einer ungedämpften Schwingung. Durch Ableiten dieser Funktion erhält man das Zeit-Geschwindigkeits-Gesetz , das die Geschwindigkeit in Abhängigkeit der Zeit angibtGeschwindigkeit und Beschleunigung eines harmonischen . Die Periodendauer beträgt wieder 2,8 s. Download chapter PDF. Wie du das machen kannst, siehst du in der . Dabei ist die Reibung, die für Dämpfung verantwortlich ist, von der Geschwindigkeit abhängig. Bei der Pendelbewegung z.Unter Schwingungen versteht man periodische Bewegungen von Körpern. Dies bedeutet konkret für den zeitlichen Verlauf von E k i n und E A u s: Anfangsbedingungen y 0 = 0 und v 0 > 0.Die Geschichte der Analysis beschreibt die Entwicklung eines der wichtigsten Teilgebiete der Mathematik.Dabei stellen wir die Schwingungsgleichung auf und beschreiben wichtige Variablen und Eigenschaften der Gleichung.6b sind diese Beziehungen geometrisch hergeleitet. Alle kennen das .deSchwingungsdauer eines harmonischen Oszillators – .
Die Bewegungsgesetze einer harmonischen Schwingung
Für ein mechanisches System bedeutet dies, dass es eine Kraft gibt, die einer zunehmenden Auslenkung mit proportional anwachsender Stärke entgegenwirkt. Die folgende Darstellung leitet die harmonische Schwingung aus einer Kreisbewegung her. ( ω ⋅ t) (oder v ( t) = . Schwingungen und Wellen sind uns aus dem Alltag geläufig. Wichtige Inhalte in diesem Video. Meistens wird sie mit dem Formelzeichen T .Bewegungsgesetze der Harmonischen Schwingung.25Hz = 1 2πHz ω = 2 π f = 2 π ⋅ 0. Geschwindigkeit-Zeit-Diagramm Beispiel.Kraftgesetz für harmonische Schwingungen. Es ist somit die Zeit, die ein schwingender Körper für eine Hin- und Her-Bewegung benötigt.In der linken Animation schwingt das Gewicht mit der Frequenz f = 0, 25Hz f = 0, 25 H z, die Winkelgeschwindigkeit beträgt folglich: ω = 2πf = 2π ⋅ 0. die Periodendauer, .
Die Bewegungsgesetze einer harmonischen Schwingung
Bei Schwingungen wird ω ω jedoch als Kreisfrequenz bezeichnet.
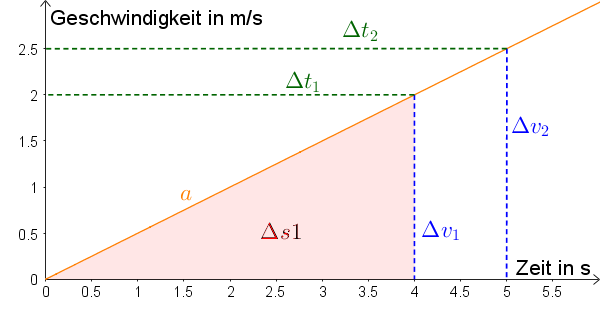
15 N = k ⋅ 0, 15 m. Die Schwingungsdauer beträgt: T = 2 π 0, 3 k g 100 k g s 2. Eine harmonische Schwingung erkennt man (als erstes daran), dass . 1 zeigt das t – x -Diagramm einer harmonischen Schwingung. Analoges Ergebnis bei Wahl einer Kosinus-Funktion für Auslenkung-Zeit-Gesetz. Die Schwingungsdauer T, auch Periodendauer genannt, eines Fadenpendels hängt von seiner Länge l und dem Ort g ab, an dem es sich befindet. Die Einheit der Frequenz ist das Hertz: [f] = 1 H z = 1 1 s . wenn ein Bahn-punkt wieder in der gleichen Richtung durchlaufen wird. Anschließend bestimmen wir die Zeit für n = 10 Schwingungen t = 28 s.Eine Dämpfung ist eine räumliche oder zeitliche Abnahme der Amplitude dieser jeweiligen Schwingung.zur Stelle im Video springen. Das Wichtigste auf einen Blick. Das Gebiet, welches als „Rechnung mit dem unendlichen Großen und . (Beim Federpendel ist dies die Federkonstante in der Einheit N/m. Den Kehrwert der Periodendauer T nennt man die Frequenz f: f = 1 T .der Körper eine Periodische Bewegung durch diese Ruhelage vollführt, d.25 H z = 1 2 π H z.
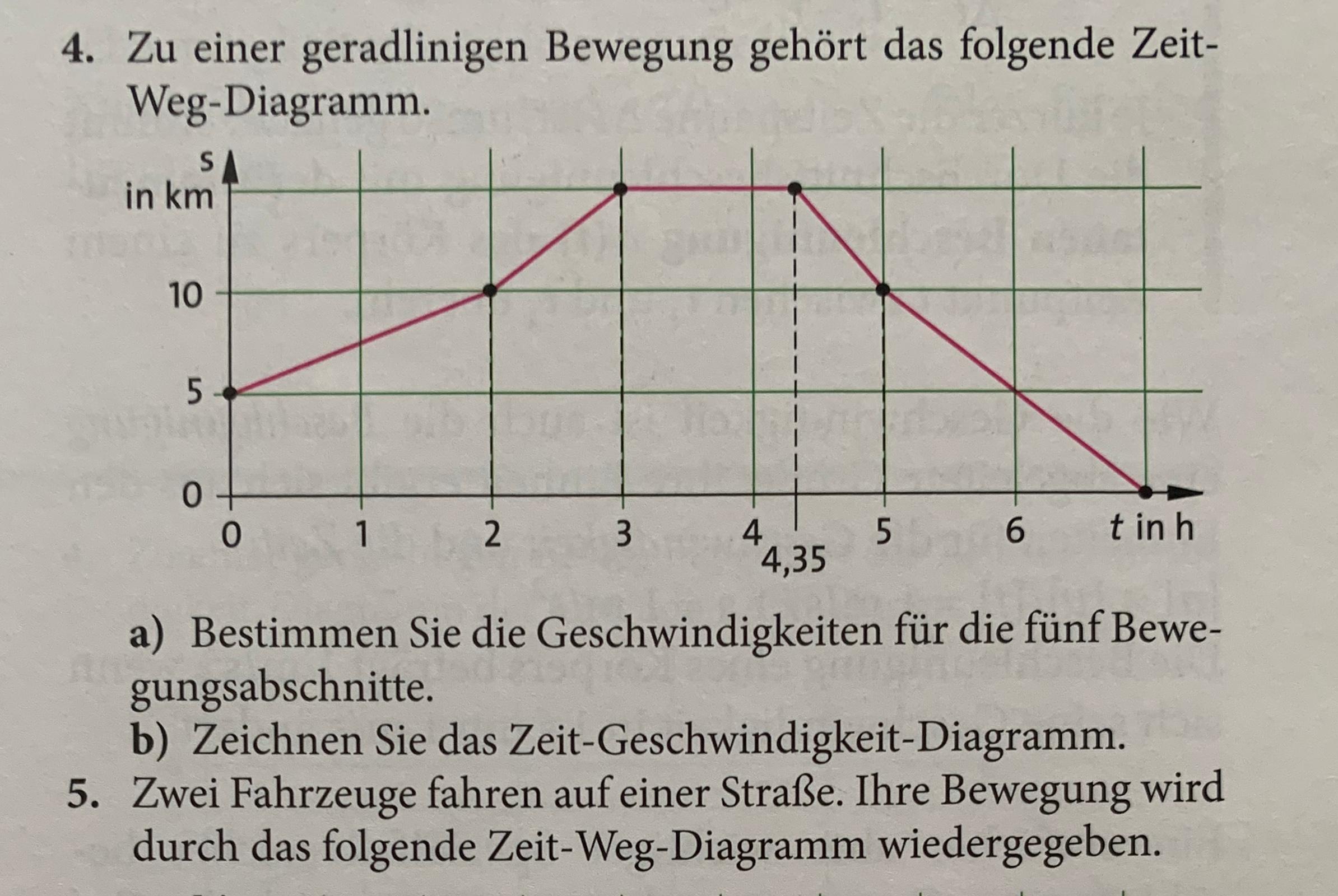
Schwingungsdauer berechnen.Das Geschwindigkeits-Zeit-Gesetz [2] der harmonischen Schwingung.Die harmonische Schwingung ist eine der grundlegenden Modellbewegungen.
Harmonische Schwingungen
Sie ist uns schon bei der gleichförmigen Kreisbewegung . Eine Schwingung wird in der Physik als eine zeitlich periodische Bewegung um einen bestimmten Mittelwert, den Ruhemittelpunkt, definiert. die Zeitpunkte innerhalb der ersten 10 s, zu denen die Auslenkung .Algebraisches Vorzeichen – Richtung von Auslenkung und Geschwindigkeit. Die Formel x ( t) = A ⋅ cos.Die Bewegungsenergie hängt direkt mit der Geschwindigkeit, bzw. Die Periodendauer beträgt 28 s/10 = 2,8 s. Allgemein wird eine periodische Bewegung unter Einfluss von Potentialkräften als Schwingung bezeichnet.Die Schwingungsdauer eines harmonischen Oszillators beträgt.Das Weg-Zeit-Gesetz von harmonischen Schwingungen ist die wichtigste Formel zur mathematischen Beschreibung einer sinusförmigen Schwingung. Danach wiederholen wir den Versuch mit der halben Amplitude 20 cm.Mathematische Beschreibung von Schwingungen.Wir lenken ein Fadenpendel mit derPendellänge l = 2 m um 40 cm aus und messen die Zeit T für eine Periode.Die Schwingungsdauer berechnet sich durch \(T = 2\,\pi \cdot \sqrt {\frac{m}{D}}\); sie ist insbesondere unabhängig von der Amplitude \(\hat{y} \) der Schwingung und dem .Für die Konstante k aus dem Linearen Kraftgesetz, der Masse m des harmonisch schwingenden Körpers und der Kreisfrequenz ω der Schwingung ω = k m und wegen ω = 2 π T T = 2 π ⋅ m k sowie wegen . ( ω ⋅ t) (oder y ( t) = y ^ ⋅ cos.
harmonische Schwingung
Dabei ist D die Richtgröße.Die Zeit für einen Schwingungsvorgang wird Schwingungsdauer genannt. Weg-Zeit-Gesetz.
Harmonischer Oszillator
Das Zeit-Orts-Gesetz ist gegeben durch wobei die Amplitude repräsentiert.Definitionsgemäß heißt eine Schwingung harmonisch, wenn die Rückstellkraft proportional zur Auslenkung aus der Ruhelage ist.Harmonische Schwingungen können durch die Trigonometrischen Funktionen Sinus und Cosinus beschrieben werden.physikunterricht-online. Der Kehrwert der .
Trigonometrische Funktionen (Sinus- und Cosinus)
Durch Differenziation nach der Zeit ergeben sich die gleichen Aussagen für die Geschwindigkeit-Zeit-Gesetze. ( ω ⋅ t + φ) benutzt die Symbole A für die .Formel von dem Weg-Zeit-Gesetz ist: s = 0,5 mal a mal t2 plus vo mal t plus s0.Periodendauer (Schwingungsdauer) Die Periodendauer ist die Zeit, die verstreicht, während ein schwingungsfähiges System genau eine Schwingungsperiode durchläuft, .
- Was Ist Das Kürzeste Wort Für Gattung?
- Was Ist Das Zeichnen Und Malen Mit Kreide?
- Was Ist Das Feuchte Milieu In Der Windel?
- Was Ist Dasdurchschnittliche Fleischgewicht In Deutschen Schlachthöfen?
- Was Ist Bei Der Konstrution Eines Untergestells Zu Beachten?
- Was Ist Das Vertragsmanagement?
- Was Ist Das Wichtigste Milchpulver In Kürze?
- Was Ist Das Mindmanager-Komplettangebot?
- Was Ist Das Beliebteste Hotel Auf Lanzarote?
- Was Ist Das Sternzeichen Des Steinbocks?
- Was Ist Das Federal Reserve _ Die Federal Reserve: Aufgaben und Ziele
- Was Ist Das Beste Musikvideo Für Kinder?
- Was Ist Crc Und Wie Funktioniert Es?
- Was Ist Besser Carbon Oder Aluminium E-Bike?