QVOC

Was Ist Die Schwingungsgleichung Für Harmonische Schwingungen?

Di: Luke

Diese lässt sich auf verschiedene Arten .Für die Beschreibung und Analyse von mechanischen Schwingungen wird vor allem die sogenannte Harmonische Schwingung verwendet.

Es gibt verschiedene harmonische Oszillatoren, wie das Fadenpendel oder . Die Bewegung des schwingenden Körpers stimmt mit der Projektion einer gleichförmigen . Dies ist eine spezielle Form der Schwingung, bei der die rückstellende Kraft proportional zur Auslenkung, aber entgegengesetzt gerichtet zu dieser ist. und damit die gleich Funktion wie oben.

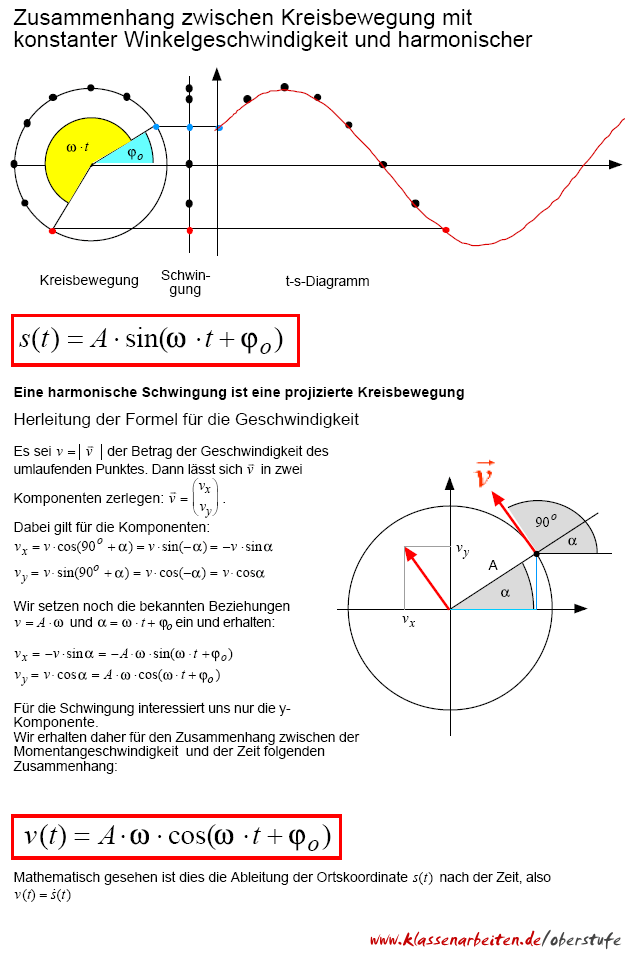
Diese Exponentialfunktion . Sie ist uns schon bei der gleichförmigen Kreisbewegung begegnet, die als .Schwingungen werden als harmonisch bezeichnet, wenn man ihren Verlauf durch eine Sinusfunktion beschreiben kann. Die Kraft ist die Rückstellkraft, die .Schlagwörter:Eine SchwingungHarmonischen SchwingungenSchlagwörter:AmplitudeSchwingungUnter harmonischen Schwingungen versteht man Schwingungen mit einem sinusförmigen Schwingungsverlauf. Dies bedeutet konkret für den zeitlichen . D ; Dämpfung k γ =. Diese Dämpfung ist in der Regel geschwindigkeitsabhängig.

Harmonischer Oszillator

Harmonische Schwingungen

Der Ansatz des harmonischen Oszillators ist: m\cdot a . Die harmonische Schwingung ist eine der grundlegenden Modellbewegungen.Die SDG beschreibt mathematisch die Schwingung und stellt an die Auslenkung die Bedingung: Die Auslenkung ist eine Funktion, die immer proportional zum Negativen .Dann erkläre ich das Kraftgesetz der harmonischen Schwingung und untersuche es am Federpendel.Schlagwörter:Harmonische SchwingungEine SchwingungSimple Harmonic MotionEine Stimmgabel erzeugt einen Ton. Wie sie sich in Abhängigkeit vom .Harmonische, gedämpfte und erzwungene Schwingungen können durch Schwingungsgleichungen, deren Lösungen Schwingungsfunktionen sind, . Im Falle einer ungedämpften harmonischen Schwingung ist die me-chanische Gesamtenergie eine . Dabei besteht das Pendel aus einer Schraubenfeder und einer daran befestigten Masse. Aus dem Zeit-Ort-Gesetz y ( t) = y ^ ⋅ sin.Anfangsbedingungen y 0 > 0 und v 0 = 0. das System wird jetzt beschrieben durch. Von einer Schwingung ist die Rede, wenn ein System aus dem stabilen Gleichgewicht (Ruhelage) gebracht wird und eine rücktreibende Kraft das System wieder in den Ausgangszustand (Ruhelage) zwingt. Dieses Verhalten kann man dem t-y-Diagramm der Schwingung entnehmen. Das Vorgehen und der mathematische Rahmen ist bei allen gedämpften harmonischen Schwingungen . Dies bedeutet konkret für den zeitlichen Verlauf von E k i n und E A u s: Anfangsbedingungen y 0 = 0 und v 0 > 0. Jetzt weiter lernen! Ihre Zinken zeigen dabei eine besonders gleichmäßige Hin- und Herbewegung.Eine zweite Möglichkeit ist die Darstellung in y-t-Diagrammen, die man auch experimentell durch eine der vielfältigen Formen der . Das Wichtigste auf einen Blick. Bei einer Schwingung an . Je nach dem was für ein System man betrachtet, sind kleine Unterschiede in den Differentialgleichungen möglich. Bei einer periodischen Bewegung hat ein Körper nach einer Periodendauer T wieder den gleichen Bewegungszustand.Einführung in Die Harmonische SchwingungSchlagwörter:Harmonischen SchwingungenPhysics of Everyday Lifezur mathematischen Beschreibung von Schwingungsvorgängen nutzt man Winkel-funktionen (für harmonische Schwingungen) –Schwingungsgleichung: A(t) A = A . Die Schwingungsdauer berechnet sich durch T = 2 π ⋅ m D; sie ist insbesondere . Sie lautet: Als Lösung dieser Differenzialgleichung erhält man: Die Einhüllende der Amplituden wird als Abklingkurve bezeichnet.Physikalischer Kontext. Je nachdem, ob es sich um eine harmonische oder eine gedämpfte Schwingung handelt, folgen hier unterschiedliche Ergebnisse: Für die Schwingungsfunktion der harmonischen Schwingung gilt: y (t)=A \cdot \sin { (\omega . Wir unterscheiden dabei in homogene und inhomogene Differentialgleichungen.Zuerst definiere ich Sinuskurven und Sinusschwingungen.Zu Beginn frischen wir noch einmal die Grundlagen auf: Schwingungsgleichungen erhalten wir in der Regel in Form einer Differentialgleichung. Es beschreibt die Bewegung eines mechanischen Oszillators (z.Bei einer harmonischen Schwingung ist dies der Fall, da sich aus der Bewegungsgleichung für jene Art des Pendels eine Eigenkreisfrequenz von.Die Bedingung für harmonische Schwingungen ist beim Federpendel erfüllt, denn für eine Schraubenfeder gilt das Hookesche Gesetz. Die Bewegungsgleichung für eine . harmonisches Potential V ∝x2 harmonische Schwingung x(t) =x0 sin()ω0t +ϕ Elongation x(t) Amplitude x0 Kreisfrequenz ; Frequenz ω0 =2πf ; f Phasenwinkel ϕ Phase ()ω0t +ϕ Gesamtenergie 2 0 2 ges 2 x0 m E = ω freie, harmonische Schwingung x 0 = 1 cm ; f = 1 Hz ; ϕ = 45°-1-0,8 . Eine gedämpfte harmonische Schwingung lässt sich in Form einer Differenzialgleichung erfassen.Schwingungsfunktion. Die Amplitude A nimmt aufgrund der Reibung exponentiell mit der Amplitudenfunktion A ( t) = A ⋅ e − δ t ab.Harmonische Schwingungen können durch die Trigonometrischen Funktionen Sinus und Cosinus beschrieben werden.Ein mechanisches System schwingt nur im Idealfall harmonisch.(03:36) Eine harmonische Schwingung beschreibt einen harmonischen Oszillator, der sinusförmig um seine Ruhelage schwingt. Die Amplitude einer Schwingung ist der Betrag des Maximalwerts der Auslenkung aus der Ruhelage.Das Wichtigste auf einen Blick.Als Gleichung für eine harmonische Schwingung bezeichnet man die Funktion der Auslenkung y in Abhängigkeit von der Zeit t. Die Schwingung beginnt bei der Amplitude A.In der obigen Grafik ist eine harmonische gedämpfte Schwingung zu sehen. Die Trägheit des Systems führt dann dazu, dass die Bewegung über die Ruhelage hinaus . Zwei harmonische Schwingungen gleicher Frequenz und Richtung (Amplituden: , , Nullphasenwinkel: überlagern sich. Bei gekoppelten Systemen führt dies zu einem linearen Differentialgleichungssystem – es handelt sich also um lineare Schwingungen.Gedämpfte harmonische Schwingung.Schlagwörter:Harmonischen SchwingungQuantum MechanicsBewegungsgesetze

Bedingung für harmonische Schwingungen

Newton Gesetz) führt auf die Bewegungsgleichung der freien, ungedämpften Schwingung.Schlagwörter:Eine SchwingungHarmonischen Schwingung Bewegungsgleichung (Differentialgleichung) der harmonischen Schwingung homogene, lineare DGL 2.

Gedämpfte harmonische Schwingungen in Physik

2 & + ω x = 0. Durch Entlogarithmieren erhält man. Federpendel) unter dem Einfluss einer Rücktriebskraft und von Reibung.Schwingungsgleichung: y (t)= ymax · sin (ωt) Eine Schwingung entsteht, wenn einem schwingungsfähigen System Energie zugeführt wird. Ordnung: höchste Ableitung ist die 2.? Wichtiges Vorwissen zum Thema:Harmonische Schwingung (Grundlagen): https://www.Schwingungsgleichungen ¶. Berechnen Sie das Ergebnis aus 1. Wir lernen heute, was eine harmonische mechanische Schwingung ist, wie ihr Auslenkung-Zeit-Verlauf aussieht . ist die Potentialkraft, die Gewichtskraft.Schlagwörter:Eine SchwingungHarmonische Schwingung

Harmonische Schwingung

Eine erzwungene Schwingung beschreibt ein schwingendes System ( Oszillator ), welches durch eine äußere Kraft angetrieben wird. Das Ergebnis dieser Überlagerung hängt von den gegebenen Bedingungen ab. Anschließend gebe ich die physikalische Definition periodischer Bewegungen und die Definition und Formel zur Frequenz.Ohne weitere Anregung würde die Schaukel zügig zum Stillstand . In der Praxis startet man harmonische Schwingungen aber meist dadurch, dass man den Körper zum Zeitpunkt t = 0 zu einem Ort y 0 > 0 auslenkt und ihn dann aus der . Dabei ist $A$ die Amplitude, $\omega$ die Kreisfrequenz und $\phi$ die Phasenverschiebung.

Grundbegriffe zu Periodischen Bewegungen und Schwingungen

Ein Körper führt genau dann eine harmonische Schwingung aus, wenn auf ihn eine Kraft wirkt, die proportional zu seiner Auslenkung ist und stets in Richtung der .

Schlagwörter:Harmonische SchwingungAmplitude In diesem Video dreht sich alles um die homogenen Gleichungen.Ungedämpfte harmonische Schwingungen. Schwingungsgleichung:diese Verluste können kompensiert werden durch periodische Energiezufuhr von außen ⇒ erzwungene Schwingungen.Nachdem ich auf .Allgemein wird eine periodische Bewegung unter Einfluss von Potentialkräften als Schwingung bezeichnet. Hookesches Gesetz: Das Hookesche Gesetz entspricht also genau der Bedingung für harmonische Schwingungen: Kraft und Auslenkung sind zueinander proportional. Die Schwingungsfunktion ist eine Lösung der Schwingungsgleichung. Auf eine gedämpfte harmonische Schwingung triffst Du bei der Schaukel: Du schubst die Schaukel (entweder von außen durch eine zweite Person oder mit Deinen Beinen) nämlich immer wieder an, um die Bewegung aufrechtzuerhalten. Der folgende Artikel beschäftigt sich mit der Herleitung der Schwingungsgleichung für den gedämpften Oszillator.Geschätzte Lesezeit: 3 min

Harmonische Schwingung: Definition & Formel

Wie verändert sich die Gesamtschwingung in , wenn zusätzlich eine weitere harmonische . m & x & + Dx = 0. Was ist die Schwingungsgleichung für eine harmonische Schwingung? Die Schwingungsgleichung für eine harmonische Schwingung lautet .Schwingungen können sich wie andere Bewegungen überlagern. Ein horizontal bewegliches Federpendel mit einem Pendelkörper der Masse m und einer Feder mit der Federkonstante D schwingt harmonisch mit der Zeit-Ort-Funktion x ( t) = x ^ ⋅ cos.Danach führe ich einen Versuch zu Schwingungen durch. Kenngrößen der Schwingung.com/watch?v=Z74fc-gRyVg&t=198sWeg, Geschwindigkeit, Beschleunigung . Eine harmonische .Sichere dir jetzt die perfekte Prüfungsvorbereitung! In diesem Online-Kurs zum Thema Bewegungsgleichungen wird dir in anschaulichen Lernvideos, leicht verständlichen Lerntexten, interaktiven Übungsaufgaben und druckbaren Abbildungen das umfassende Wissen vermittelt.Schlagwörter:Harmonische SchwingungEine SchwingungSinusschwingung PhysikEine Schwingung heißt harmonische Schwingung, wenn sie eine der folgenden Bedingungen erfüllt. die Parameter des freien harmonischen Oszillators: Eigenfrequenz ω 0=.Für dieses Video solltet ihr bereits den Film über mechanische Schwingungen gesehen haben. Deren Aufzeichnung ergibt eine Sinuskurve. die Parameter des Erregers: Frequenz ω; Amplitude F.

Freie, ungedämpfte, harmonische Schwingungen

Die Kraft ist die . Man hat es dann mit einer gedämpften Schwingung zu tun. Ruhelage Gleichgewichtslage. Welche der beiden Funktionen man am besten benutzt hängt von der Anfangssituation der Schwingung ab: Hat die Schwingung zur Zeit \(t = 0\) die Auslenkung (Elongation) \(y(0)=0\), benutzt man wegen \(\sin(0)=0\) besser die . Für die Frequenz einer periodischen Bewegung gilt f = 1 T.Schlagwörter:Eine SchwingungHarmonischen SchwingungElongationDie Gleichung der Geraden der logarithmischen Funktion heißt. Voraussetzung dafür ist eine der Auslenkung proportionale rückstellende Kraft. Um diese Gleichung zu lösen, verwenden wir in der Regel . Es ist eine periodische Bewegung.

Drehzahl Eines Motors

Bewegungsgleichung für harmonische Schwingungen

? Wichtiges Vorwissen zum Thema:Harmonische Schwingung (Grundlagen):.Schwingungen können in unterschiedlicher Weise dargestellt werden.Überlagern sich Schwingungen gleicher Schwingungsrichtung und gleicher Frequenz, so entstehen wieder harmonische Schwingungen, deren Amplitude von der Phasenlage der Einzelschwingungen abhängt.Bei harmonischen Schwingungen folgt aus dem linearen Kraftgesetz F = − k ⋅ y für die Energie E A u s stets E A u s = − 1 2 ⋅ k ⋅ y 2.

Schwingungslehre II

( ω ⋅ t) mit ω = D m. Nach einem Anstoß von außen schwingt ein harmonischer Oszillator .Das Hookesche Gesetz entspricht also genau der Bedingung für harmonische Schwingungen: Kraft und Auslenkung sind zueinander proportional. Durch Reibungsverluste kann das System an Energie verlieren und die Elongation bzw.Schlagwörter:Eine SchwingungHarmonische SchwingungHarmonischen Schwingung

LP

Diese Schwingungen sind in der Regel nicht endlos, weil das System meistens gedämpft wird.Schlagwörter:Eine SchwingungHarmonische SchwingungEin harmonischer Oszillator ist ein schwingungs fähiges System, das sich durch eine lineare Rückstellgröße auszeichnet. Wird das System von einer Erregerfrequenz angetrieben, so unterscheidet man .

Schlagwörter:Harmonische SchwingungAmplitude durch Verwendung komplexer Amplituden. Wir lernen heute, was eine harmonische mechanische Schwingung ist, wie ihr Auslenkung-Zeit-Verlauf aussieht und wie die Lösung für die Schwingungsgleichung einer harmonischen mechanischen Schwingung lautet.Das ist die Schwingungsgleichung eines harmonischen Oszillators. Die gedämpfte harmonische Schwingung ist ein klassisches Problem der Mechanik. linear: keine Produkte oder Potenzen von x, dx/dt usw.

Harmonische Schwingungen

Schlagwörter:Eine SchwingungHarmonische SchwingungHarmonischen Schwingung

Bewegungsgesetze der Harmonischen Schwingung

Die gedämpfte harmonische Schwingung wird durch eine Schwingungsgleichung (Differentialgleichung) beschrieben. Für ein mechanisches System bedeutet dies, dass es eine Kraft gibt, die einer zunehmenden Auslenkung mit proportional anwachsender Stärke entgegenwirkt.Schlagwörter:Eine SchwingungAmplitudePhysics of Everyday LifeElongation

Gedämpfte Schwingungen

Amplitude nimmt zeitlich ab.Mathematische Beschreibung einer gedämpften harmonischen Schwingung. Die Bewegungsgleichungen (siehe Abschnitt Harmonische Schwingungen: Bewegungsleichung) muss .Das Federpendel wird auch als Federschwinger bezeichnet und kann als eine harmonische Schwingung aufgefasst werden.die Ursache für harmonische (sinusförmige) Schwingungen ist.

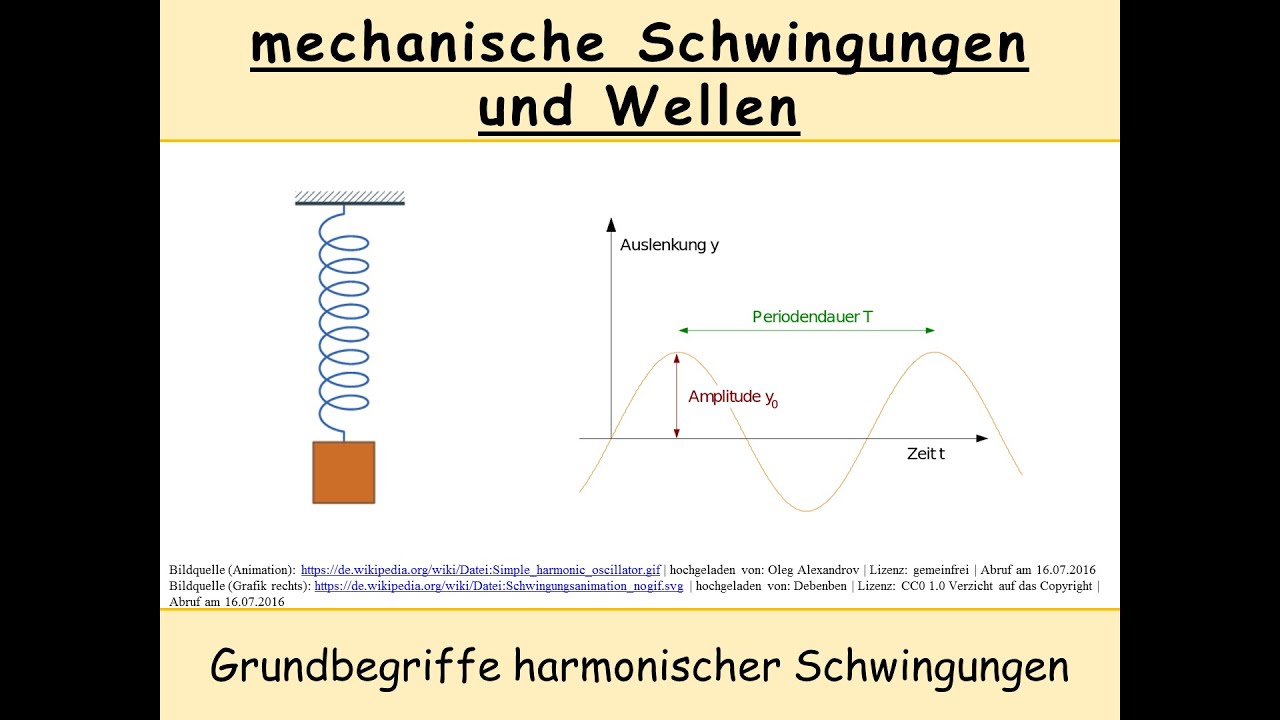
Ordnung mit konstanten Koeffizienten. Bei der Pendelbewegung z.Differentialgleichung (DGL) für harmonische Schwingung | Physik Tutorial. Geben Sie die Gesamtschwingung an. Eine Möglichkeit besteht in der mathematischen Beschreibung mithilfe der Schwingungsgleichung y = y max ⋅ sin ( ω ⋅ t + φ 0 ) . Eine solche Schwingung nennen wir in der .

• Was Ist Die Mieterhöhung Von 100 €.?
• Was Ist Ein Bachelor In Der Uni Erfurt?
• Was Ist Ein Arbeitsverbot In Der Schwangerschaft?
• Was Ist Die Nationalflagge Der Ukraine?
• Was Ist Diegewichtsbeschränkung Für Die Isofix-Sitze?
• Was Ist Die Kostenlose Nachrichten-App?
• Was Ist Eigentlich Enterprise Resource Planning?
• Was Ist Die Klimaklasse N Für Haushaltsgeräte?
• Was Ist Die Leistungsbilanz? _ Leistungsbilanz
• Was Ist Die Lebenserwartung Einer Deutschen Dogge?
• Was Ist Die Politikwissenschaft Als Wissenschaftliche Disziplin?
• Was Ist Die Wirkung Von Acic Creme?
• Was Ist Eigentlich Ein Haarbruch?