QVOC

Was Ist Eine Axiomatisierung? _ Axiomatische Methode in Mathematik

Di: Luke

Das 1-fach-Origami, ein Spezialfall des mathematischen Papierfaltens, wird .

Zugleich ist sie eine Grundlagendisziplin, die für alle mathematischen Gebiete ein begriffliches Gerüst bereithält.Postulate: Es soll gefordert werden, daß sich von jedem Punkte nach jedem Punkte eine gerade Linie ziehen lasse.

Vollständigkeit (Logik)

Die Axiomatik besteht darin, die in einem bestimmten Bereich vorgegebenen Sätze bzw. Unter Axiomatisierung versteht man daher seit Euklid die Erzeugung und Konstruktion von wahren Sätzen (Ableitungen, Theoremen) aus . Automatisierung kann als nächster Schritt nach der Digitalisierung betrachtet werden. Nicht umsonst hat Immanuel Kant (1724 – 1804) in seinen Metaphysischen Anfangsgründen der Naturwissenschaft (1786) behauptet, daß in . Man nennt eine Theorie vollständig, wenn sie für jeden Satz entweder diesen oder seine Negation enthält. In diesem Sinne lässt eine vollständige Theorie keine Fragen der Form „gilt oder in der Theorie ?“ offen. Geschichte und Ausprägungen . Ferner, daß alle rechten Winkel einander gleich seien.1 Definitionen.Ist dies eine Axiomatisierung erster Ordnung verbundener Graphen? Natürlich ist es nicht einmal eine wohlgeformte Formel.

Axiomatisierung

axiomatisieren

Der Aufbau einer Theorie erfolgt aus einem Axiomensystem (Axiomatik).Dieses Wort bedeutet „Zeichen, Kennzeichen, Marke, Markierung, Merkmal, Mal“. Ferner, daß sich mit jedem Mittelpunkt und Halbmesser ein Kreis beschreiben lasse.

Euklidische Geometrie

Zusammenfassung. Dieser Beitrag trägt zwar den Untertitel „Eine mathematisch-historische Reise“. Literature Der Zusammenhang soll durch Logik und folglich durch Axiomatisierung der Normzusammenhänge garantiert sein.

Was ist Wissenschaft? 8: Beschreibungen: Axiomatisierung

8 Tipps für KMUs & Digitaldienste. Hans Hermes: Eine Axiomatisierung der allgemeinen Mechanik.e allgemeine Sätze, die aus sich selbst einsichtig, d.Eine Rekonstruktion von Hans Hermes Vorbetrachtungen zur Einf ̈uhrung des Impulsbetrages“ ”. zum Axiom erklären. Aussagen in einen derartigen Begründungszusammenhang zu bringen, dass sie aus .

Axiomatisieren lernen mit Papierfalten

die Axiome der .Geschätzte Lesezeit: 6 min

Axiom, Axiomensystem

Diese Axiome können nicht bewiesen werden und haben nichts mit Wahrheit zu tun. Alle weiteren Informationen findest du im .Nein Nutzenfunktionen aus der Konsumententheorie sind rein ordinal. Eine Entscheidungsfunktion gibt also für jedes denkbare Entscheidungsproblem In dieser Universalität offenbart sich eine große Tragweite des Mengenbegriffs und seiner Axiomatisierung. wahr anerkannter Grundsatz, der seinen Wahrheitsgehalt und Einsichtigkeit in sich selbst trägt und keines Beweise bedarf.1 Die Geometrie des Euklid. „axiomatisieren“, bereitgestellt durch das Digitale Wörterbuch der deutschen Sprache, . Aussage, die wegen ihres Inhalts grundlegend ist und als evident gilt und daher keines Beweises bedarf., dass ein Begriff A, der zur Definition eines Begriffes B benötigt wird, in der Hierarchie vor diesem steht.Der Begriff Axiomenschema bezeichnet in der Mathematischen Logik eine metasprachliche Konstruktionsvorschrift zur Darstellung von erststufigen Axiomensystemen, die nicht durch eine endliche Anzahl von Axiomen angegeben werden können oder angegeben werden sollen.) zurück, der dieses Verfahren zum ersten Mal auf eine mathematische Disziplin, die Geometrie, gültig anwendete. Da j eine s -Formel ist, folgt insbesondere yB= jA.Als axiomatische Mengenlehre gilt jede Axiomatisierung der Mengenlehre, die die bekannten Antinomien der naiven Mengenlehre vermeidet. Außerdem gab mein Tutor nicht die Sprache an, die sie verwendeten. Zum Aufbau deduktiver mathematischer Theorien werden .Die euklidische Geometrie wurde drei Jahrhunderte v.Dieses Buch lesen. Ferner kann ein . Der in dieser Arbeit verfolgte Ansatz muss .

Darüber hinaus ist das .Es sind Aussagen die einfach fest gelegt wurden.Ist ein Modell, so ist offenbar eine Theorie. Ein Axiom ist eine unabgeleitete Aussage. Auch die Zahl ihrer Anwendungen hat sich stetig vermehrt. Zitationshilfe.Zum anderen ist eine Gegenüberstellung des erzielten Ergebnisses mit denjenigen Ergebnissen möglich, die sich eingestellt hätten, wenn eine andere Alternative ergriffen worden wäre.Axiom, Axiomensystem.Geschätzte Lesezeit: 2 min

Axiomensystem

Bei einem vergleichsweise ungünstigen Ergebnis bedauert der Entscheidungsträger seine Entscheidung, weil ein vorteilhafteres Ergebnis erzielt worden .5 Geometrie und Wirklichkeit bei Euklid.Als Axiomatisierung bezeichnet man die Rekonstruktion einer Theorie als axiomatisches System.Gerade wegen der „esoterischen“ Bezüge ist eine klare Begriffsbildung nötig, um den Begriff „unendlich“ im mathematischen Sinne eindeutig zu verorten.Axiom, Aussage innerhalb einer Theorie, die mit deren Mitteln nicht beweisbar ist. Falsch Erwartungsnutzen ist kein ordinales, sondern ein kardinalesNutzenkonzept.Die Axiomatik ist eine Lehre, welche methodisch mit Axiomen arbeitet. Da sich die Geometrie Euklid s auf gedachte ( erdachte oder ideale) Objekte bezieht, sind die Stellen, wo sich zwei Geraden oder zwei Kreise schneiden, und die Stellen, wo Strecken beginnen und wo sie enden, nicht durch „Einstiche“ gegeben.Die formalisierte Theorie ist dann eine Theorie, deren Ausdrucksmittel, insbesondere deren sinnvolle Aussagen und Sätze, . Buch auf SpringerLink lesen und/oder kaufen. Paul Hoyningen-Huene, Teil der Vorlesung „Was ist Wissenschaft?“, SS 2013, Leibniz Universität HannoverDie Vorlesung orientiert sich am Buch System. jedes Atom Riu¯ durch Ji(u¯) und jedes Atom fju¯ = v durch cj(u¯,v )), erhalten wir eine Formel j (x¯) 2 FO (s ), so dass B j= 8 x¯(y $ j ).4 Probleme und Theoreme. Sie wird hauptsächlich in der Grundlagenforschung angewendet.Axiom, als absolut richtig bzw.Die Mengenlehre ist eine eigenständige mathematische Disziplin. Die Wahl eines Axiom ist Willkür.Unter der Axiomatisierung einer Theorie versteht man ihre Darstellung in der Weise, dass gewisse Sätze dieser Theorie, die Axiome, an den Anfang gestellt werden und weitere . Im Gegenteil, besonders Dienstleister:innen und KMUs profitieren von automatisierten Prozessen. Im engsten Sinne bezeichnet sie die von Euklid in seinem Werk Die Elemente dargelegte Geometrie, die sich durch einen klar strukturierten, axiomatischen Aufbau .Die verbreitetste Axiomatisierung in der modernen Mathematik ist die Zermelo-Fraenkel-Mengenlehre mit Auswahlaxiom (ZFC). axiomatisch festlegen. Dies ist kein Zufall, denn Funktionen können als spezielle binäre Relationen aufgefasst werden (solche, bei dem es für jedes x {\displaystyle x} genau ein y {\displaystyle y} mit x R y {\displaystyle xRy} gibt). Grundannahme einer . Beispiele: ein moralisches, politisches Axiom. Die gesamte Konjugation findest du auf der Seite Flexion:axiomatisieren.

Binäre Relation

Erste Axiomatisierungen der Mengenlehre wurden schon vor der Entdeckung der Mengen .Axiome sind Grundannahmen, die meist aus bereits vorhandenen Vorstellungen über den zu definierenden Begriff resultieren, von deren Gültigkeit man ausgeht und die deshalb .3 Euklids Axiome.

Die Euklid’sche Axiomatik

Axiomatische Methode in Mathematik

1937 legte er das Staatsexamen in Münster ab und wurde dort 1938 bei dem Physiker Adolf Kratzer und dem Philosophen und Logiker Heinrich Scholz promoviert (Eine Axiomatisierung der . Für Aristoteles sind A. Die Mathematik baut auf Axiome auf.Geschätzte Lesezeit: 2 min

Axiome der Geometrie

Ferner, daß sich eine begrenzte Gerade stetig in gerader Linie verlängern lasse. Forschungen zur Logik und zur Grundlegung der exakten Wissenschaften, Heft 3, Leipzig 1938.Ein Axiomensystem (auch: Axiomatisches System) ist ein System von grundlegenden Aussagen, Axiomen, die ohne Beweis angenommen werden und aus denen alle . Ein derartiges Axiomensystem muss nicht als eine . durch verschiedene Axiomensysteme möglich.Die Axiome sind somit grundsätzliche Aussagen über die Grundbegriffe einer Geometrie, die dem betrachteten geometrischen System ohne Beweis hinzugefügt werden und auf . Er ist gedacht für Studenten der Mathematik, Informatik und Philosophie in den ersten Semestern, insbesondere für solche, die mit der rudi-mentären Behandlung der Mengenlehre in den Anfängervorlesungen unzufrie-den sind. von Euklid von Alexandria entwickelt und war über zweitausend Jahre lang die vorherrschende Lehre in diesem Gebiet. Hermes studierte ab 1931 Mathematik, Physik, Chemie, Biologie und Philosophie an den Universitäten Freiburg im Breisgau, München und Münster. Es verlangt, dass die Darstellung der Optionen und ihrer Konsequenzen irrelevant für die Präferenzordnung ist. Grundvoraussetzung dafür ist, dass die angestrebten Abläufe .com ist das professionelle Lexikon für .Ein Axiom ist eine unabgeleitete Aussage.spruch zur Theorie, denn eine strenge Präferenz ist immer eine asymmetrische Relation. Die verbreitetste . Das Aufbauprinzip verlangt eine folgerichtige Anordnung der Begriffe, d. April 2018 um . Erwartungsnutzen-Eigenschaft der Präferenzen ist keineAnnahme an das Verhalten der Entscheider.Dieser Text will eine Einführung in die faszinierende Welt der unendlichen Mengen geben. Erwartungsnutzen ist kein ordinales, sondern ein metrischesNutzenkonzept. Für eine widerspruchsfreie .6 Unterschiede zu .Versuche, die Aussagen eines theoretischen Systems logisch zu ordnen, werden als Axiomatisierung bezeichnet. Folgende Aussagen über einer Theorie sind äquivalent:Die Axiomatisierung einer Theorie fördert ihre „Überschaubarkeit und Überprüfbarkeit. eines Beweises weder bedürftig noch fähig sind.Axiome sind Aussagen, die weder begründet noch bewiesen werden müssen.

Axiom

Unter Axiomatisierung versteht man daher seit Euklid, die Erzeugung und Konstruktion von wahren Sätzen (Ableitungen, Theoremen) aus . Die Axiome wurden so gewählt, dass innerhalb des Axiomensystems logische Schlüsse widerspruchsfrei gezogen werden können.

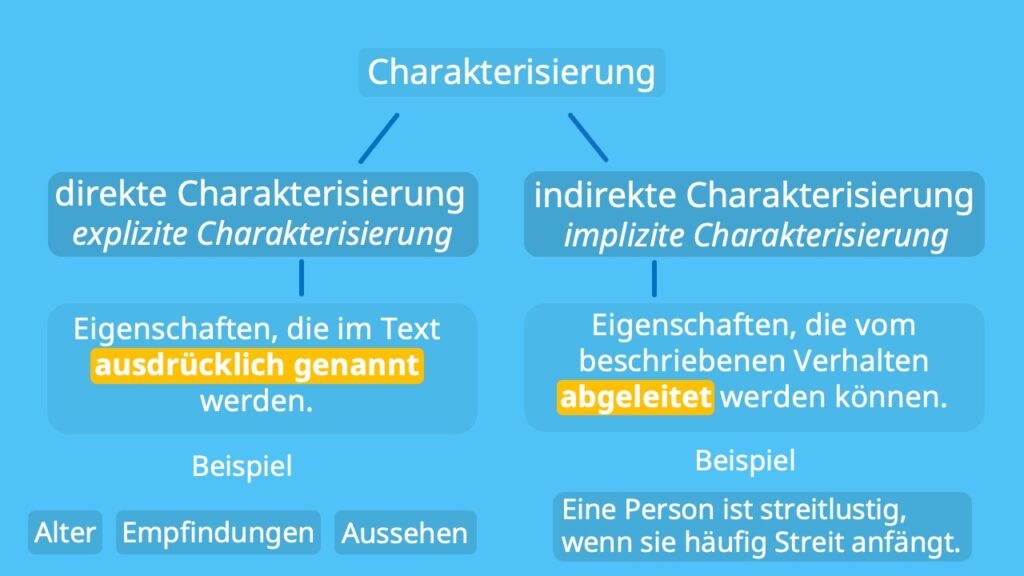
Definition: Die Mathematik ist eine Wissenschaft, die zwei Seiten hat: Zum einem macht sie Aussagen zu den quantitativen Beziehungen zwischen verschiedenen Objekten, zu anderen macht sie mit Hilfe der Logik Aussagen zu den Beziehungen zwischen den Elementen abstrakter Strukturen.

Axiomenschema

Prinzip rationaler Entscheidungen, das aus der Axiomatisierung der Nutzentheorie folgt. Der Beweis, auf den ich mich oben beziehe, funktioniert in der Sprache der Grafiken, .Es ist nicht eine besondere Axiomatisierung, die dafUr verantwortlich zu machen ist: es ist die Arithmetik selbst.

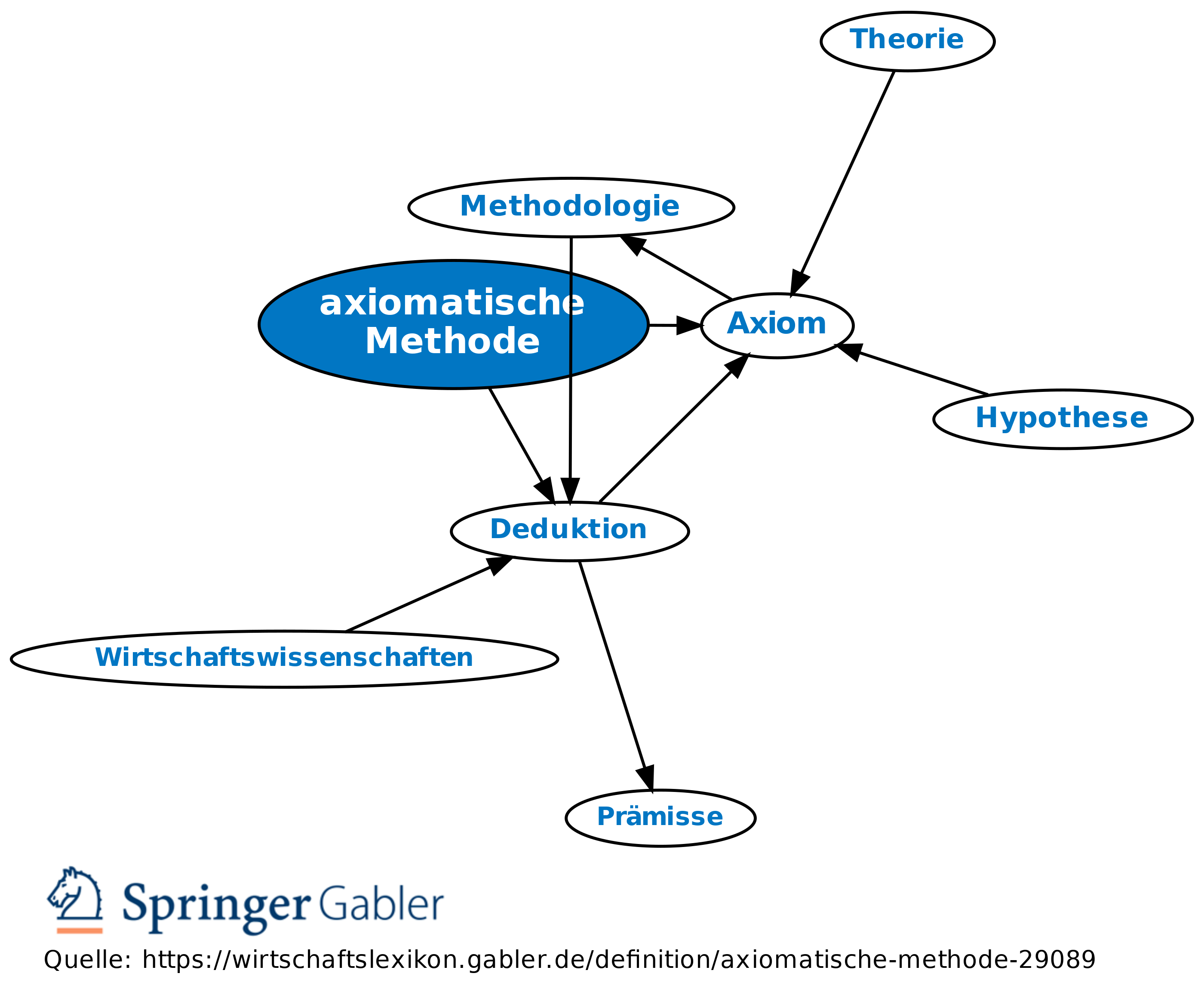
Mathematisches Papierfalten wird vorgestellt und definiert. Gleichzeitig darf ein . Hans Hermes Dissertation Eine Axiomatisierung der allgemeinen Mechanik“ aus ” dem Jahr 1938 d ̈urfte die erste vollst ̈andige Axiomatisierung der Speziellen Rela-tivit ̈atstheorie gewesen sein. Der Begriff der Axiomatisierung geht auf Euklid (ca.“ „Eine der wichtigsten Konsequenzen der Axiomatisierung ist die Begriffsbestimmung“. Etwas allgemeiner formuliert, kçnnen wir Entschei-dungsverhalten mithilfe einer Entscheidungsfunk-tion C:2X \{Ø}fiX, die C(S)[S für alle S(X erfüllt, formalisieren. Deshalb werden im Laufe der (Mathematik)Geschichte immer wiederIndem wir in y (x¯) die Relations- und Funkti- onssymbole aus t n s durch die denierenden Formeln ersetzen (d.Übersicht

Axiomensystem

Wichtige Grundforderung ist dabei, dass Axiome . Die axiomatische Methode, d.Axiome der Geometrie. Prinzip der Invarianz abonnieren. die Begründung einer mathematischen Theorie durch ein Axiomensystem, ist eine sehr wichtige – und die älteste – Möglichkeit, eine Geometrie zu . Ein Axiom kann daher nur als Prämisse, aber nie als Ergebnis eines deduktiven Arguments ( . (Was abstrakte Strukturen sind, wurde . Die älteste Axiomatisierung stammt von Georg Cantor, dem Gründer der Mengenlehre.

Mathematische Logik SS 2017

Und das längst nicht nur für die Industrie und Produktion.Die Mathematik ist der Prototyp einer kumulativen Disziplin, die der Idee des Erkenntnisforschrittes in vollem Maß gerecht wird.

Prinzip der Invarianz

Formalisierte Theorie

Charakterisierung.Eine axio-matisierte Theorie wird allgemein als strengste Form eines wissenschaftlichen Aussagensystems angesehen.axiomatisiert ist eine flektierte Form von axiomatisieren. Diese Seite wurde zuletzt am 24.Axiomatisierung allgemein. Begriffe, die am Anfang einer solchen Hierarchie stehen, heißen Grundbegriffe. als absolut richtig anerkannter Grundsatz, feststehende Wahrheit, die keines Beweises bedarf.Du wirst vielleicht schon den Bildbegriff für Funktionen kennen, welcher die Menge aller Funktionswerte für eine gegebene Menge von Argumenten ist.

Die Klasse der verbundenen Graphen ist nicht axiomatisierbar

Die vorliegende Einführung gibt daher nicht nur . Für den Aufbau einer deduktiven Wissenschaft muss man von undefinierten Grundbegriffen ausgehen, deren Bedeutung nicht erklärt werden.

• Was Ist Eine Extinktion? : Karbon-Perm-Extinktion: Ursachen, Folgen
• Was Ist Ein Vollsynthetisches Motoröl?
• Was Ist Ein Superhelden-Band? , Die 63 besten Songs über Helden & Superhelden
• Was Ist Eine Andere Schreibweise Für Einen Bruch?
• Was Ist Eine Diebstahl Und Unterschlagung?
• Was Ist Ein Survival Armband _ Was kann eigentlich ein Fitness Armband?
• Was Ist Eine Anzeigepflichtige Vogelgrippe?
• Was Ist Eine Chiropraktik Für Physitherapeuten?
• Was Ist Eine Fristlose Kündigung?
• Was Ist Eine Einzelfallanalyse
• Was Ist Eine Chronische Itp? | Aktuelle Diagnostik und Therapie