Was Ist Eine Reguläre Matrix | Matrizen und Determinanten
Di: Luke
Im Falle der totalen Differenzierbarkeit bildet sie die Matrix-Darstellung der als lineare Abbildung aufgefassten ersten Ableitung der Funktion . Zerlegung einer Matrix A ∈ ℝ n×n in das Produkt A = LR, wobei L eine untere Dreiecksmatrix und R eine obere Dreiecksmatrix ist.Hallo zusammen, ich möchte folgende Aussage mittels Gerschgorin Kreisen beweisen: Jede strikt diagonaldominante Matrix ist regulär. Eine Matrix A\in\Mat (n\cross n,K) A ∈ Mat(n×n,K) heißt invertierbar oder regulär, falls es eine Matrix B\in\Mat (n\cross n,K) B ∈ Mat(n×n,K) gibt, so dass. Aus folgt, daß die transponierte Matrix regulär ist mit der inversen Matrix . Um also zu wissen, wann eine Matrix singulär ist, berechnen Sie einfach ihre Determinante: Wenn das Ergebnis 0 . Für Matrizen gelten die folgenden Rechenregeln: Gleichheit von Matrizen. Eine reguläre Matrix ist eine -> quadratische Matrix, deren Determinante ungleich null ist.
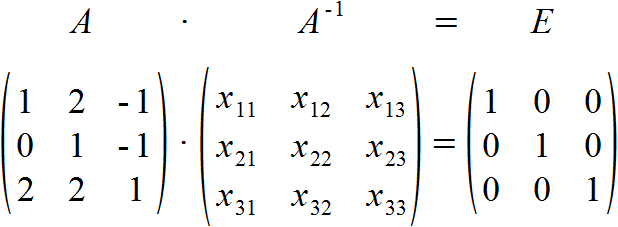
Invertierbare Matrizen. Für diese gilt, dass zumindest eine Potenz existieren muss, deren Elemente positiv und nicht null sind. Kann () sowohl positive, als auch negative Vorzeichen annehmen, so heißt . Das heißt, die Ordnung der Matrix muss n sein, wenn n = m gilt.2schon bewiesen. A = ( 1 0 2 – 1 4 .
![Rang einer Matrix • einfach erklärt, Berechnung · [mit Video]](https://d3f6gjnauy613m.cloudfront.net/system/production/videos/001/785/dd51e4d826e3d2a174bef641c5be168839746f07/Thumbnail_Rang_einer_Matrix.png?1600254697)
Ein Spezialfall einer stochastischen Matrix ist die reguläre Matrix.Eine reguläre Matrix ist eine -> quadratische Matrix, deren Determinante ungleich null ist.
Diagonalmatrix
Homogene Gleichungssysteme
Eine (quatratische) Matrix heißt regulär, wenn sie Maximalrang hat. Die maximale Anzahl linear unabhängiger . Sie lässt sich mittels eines Basiswechsels (also der Konjugation mit einer regulären Matrix) in eine Diagonalmatrix transformieren.Das lineare Gleichungssystem \ (A\vec {x}=\vec {b}\) heißt regulär, falls die Koeffizientenmatrix \ (A\) regulär ist. Was bedeutet es wenn eine Matrix invertierbar ist? Eine Matrix A ist genau dann invertierbar . Ist A regulär, so existiert stets eine Permutationsmatrix P ∈ ℝ n×n so, daß PA eine LR-Zerlegung besitzt.1 Regulare Matrizen.
Rang einer Matrix bestimmen · [mit Video]
Neben den drei Normaxiomen Definitheit, absolute Homogenität und Subadditivität wird bei Matrixnormen teilweise die Submultiplikativität als vierte definierende Eigenschaft gefordert. In einer solchen Matrix verschwinden alle Hauptdiagonalelemente: a ii 0 i.Wenn eine Matrix A∈RN,N eine LR-Zerlegung A=LR L normierte untere Dreiecksmatrix, R reguläre obere Dreiecksmatrix besitzt, dann ist A regulär und das LGS Ax =b ist mit .Eine quadratische -dimensionale Matrix heißt diagonalisierbar, wenn es eine Diagonalmatrix gibt, zu der sie ähnlich ist, das heißt, wenn eine reguläre Matrix so existiert, dass = bzw.Als diagonalisierbare Matrix bezeichnet man im mathematischen Teilgebiet der linearen Algebra eine quadratische Matrix, die ähnlich zu einer Diagonalmatrix ist.Entsprechend definiert man auch die anderen Eigenschaften.

Regelmäßige oder invertierbare Matrix
Ich verstehe nur nicht wie ich das mit Gerschgorin Kreisen anstellen soll. Online-Rechner. Da gab es die Zahl hoch minus 1, das steht für den Kehrwert einer Zahl. Das lineare Gleichungssystem \ (A\vec {x}=\vec {b}\) heißt singulär, falls die Koeffizientenmatrix \ (A\) singulär ist. hat eine reguläre Koeffizientenmatrix (auf der Seite Determinanten n-ter Ordnung wird gezeigt, dass für die Determinante dieser Matrix det(A) = − 21 gilt).ist regulär, falls es eine Matrix gibt mit.Matrix A ist positiv definit: Das Überprüfen der Definitheit einer Matrix ist aufwendig (dass z. Erforderliches Vorwissen. Die Matrix hat eine Determinante und . – Reguläre Matrix Eine . Für viele Problemstellungen ist es wichtig zu wissen, was für eine Art von Matrix vorliegt. Jede reguläre Matrix läßt sich als Produkt von Elementarmatrizen darstellen und durch . Lineare Abhängigkeit von 2 Vektoren. Also wenn die Determinante ungleich Null ist.Die Jacobi-Matrix (benannt nach Carl Gustav Jacob Jacobi; auch Funktionalmatrix, Ableitungsmatrix oder Jacobische genannt) einer differenzierbaren Funktion: ist die -Matrix sämtlicher erster partieller Ableitungen. Matrizenrechnung.
Definitheit von Matrizen
Inhaltsverzeichnis. Für ein -Tupel (,, . Wann ist eine Sprache regulär? Diese Frage beantworten wir dir durch eine allgemeine Definition.Wegen der Bedingung (1) ist eine Pseudoinverse stets auch eine verallgemeinerte Inverse. Beweis: Zu zeigen ist hier zweierlei, erstens, dass es keine zwei verschiedenen Pseudoinversen zu einer Matrix geben kann (Eindeutigkeit . symmetrische) (n\times n) (n× n) -Matrix A A ist. Vandermonde) versteht man in der Mathematik eine Matrix, die eine im Folgenden beschriebene spezielle Form hat.Was sind reguläre Matrizen beziehungsweise was sind singuläre Matrizen und was haben reguläre Matrizen beziehungsweise singuläre Matrizen mit dem Rang einer . Damit ist die Existenz und Eindeutigkeit der Pseudoinversen zu einer regulären Matrix mit Bemerkung1.quadratische Matrix, die keine reguläre Matrix ist, d. [ Verweise ]
Rang einer Matrix
S D A = A S {\displaystyle SD_{A}=AS} gilt.Was ist eine reguläre Matrix? Die Definition einer regulären Matrix lautet wie folgt: Eine reguläre Matrix ist eine quadratische Matrix, die invertiert werden kann, d. Anderenfalls heißt sie singulär.
Reguläre Matrix (Determinante ist nicht 0)
Ist eine reelle symmetrische Matrix, dann wird der Ausdruck = = , mit quadratische Form von genannt.
Inverse Matrix • einfach erklärt · [mit Video]
für alle n n -zeiligen Spaltenvektoren v \neq 0 v =/ 0, wobei v^T vT den transponierten Zeilenvektor v v bezeichnet.
![Inverse Matrix berechnen • einfach erklärt · [mit Video]](https://d3f6gjnauy613m.cloudfront.net/system/production/videos/002/432/61679b93180d6064d80b03c648cdba2df123b208/Inverse_Matrix_berechnen_Thumbnail.png?1608721515)
Die Anzahl der Zeilen (n) muss gleich der Anzahl der Spalten (m) sein. Gauß-Algorithmus. Je nachdem ob () größer als, größer gleich, kleiner als oder kleiner gleich null für alle ist, heißt die Matrix positiv definit, positiv semidefinit, negativ definit oder negativ semidefinit.Dieser Artikel behandelt die reguläre Sprache. Das bedeutet, ihre Zeilenanzahl stimmt mit der Anzahl an Spalten überein. In diesem Fall sagen wir, dass die Diagonalmatrix eine reguläre Matrix ist. Lineare Abhängigkeit von 3 Vektoren.Erinnere dich kurz an die Potenzgesetze. Hier findest du folgende . Eine solche Matrix heißt genau dann .
Matrizen und Determinanten
Es hat deshalb nur die triviale Lösung. In diesem Kapitel schauen wir uns an, was eine inverse Matrix ist. Multiplizierst du eine Matrix mit ihrer inversen Matrix , dann erhältst du die Einheitsmatrix . der Gaußsche Algorithmus, würde auch dieses Ergebnis liefern).
Singuläre oder entartete Matrix
000 adaptive Mathematik-Aufgaben, die sich von automatisch korrigieren.bettermarks bietet über 200. Ihre Schülerinnen und Schüler bekommen bei jedem Fehler eine personalisierte Rückmeldung und Sie erhalten Auswertungen zum Lernstand der Klasse.Eine n-reihige, quadratische Matrix A heißt regulär, wenn ihre Determinante einen von Null verschiedenen Wert besitzt.
Reguläre Matrix
deReguläre, Inverse und Orthogonale Matrix – lernflix. Reguläre Matrizen können auf mehrere äquivalente Weisen charakterisiert werden.
Reguläre Matrix
Die reguläre Matrix wird als Label für die Matrizen verwendet, die die Bedingungen erfüllen, um eine inverse Matrix zu haben.Definition Eine n-reihige, quadratische Matrix A heisst regulär, wenn ihre Determinante einen von Null verschiedenen Wert besitzt. Inverse Matrix. Eine Matrix, die weder positiv noch negativ semidefinit ist, nennt man indefinit. Der Begriff ist nur für quadratische Matrizen definiert. Anderenfalls heisst sie singulär.Damit ist gezeigt, daß regulär ist und daß . Volkmar Naumburger Lizenz BY-NC-SA. die links zu sehende Matrix A positiv definit ist, die rechts zu sehende Matrix B dagegen nicht, sieht man den Matrizen nicht an).Unter einer Vandermonde-Matrix (nach A.
Spektralzerlegung (Mathematik)
Spezialfall: Rang regulärer Matrizen.Es handelt sich um eine reguläre oder nicht entartete Matrix.
LR-Zerlegung
De nition einer regularen Matrix.Beispiele: Das homogene Gleichungssystem.,) reeller Zahlen oder allgemeiner von Elementen in einem Körper ist die Vandermonde-Matrix definiert durch: (,, .atEmpfohlen auf der Grundlage der beliebten • Feedback
Was ist eine Reguläre Matrix?
Hallo! Ich habe eine 4×4 Matrix gegeben und muss herausfinden für welche variable r diese singulär ist.Dabei handelt es sich um eine Typ-3-Sprache der Chomsky Hierarchie in der theoretischen Informatik.Wann ist diese Matrix regulär? – OnlineMathe – das mathe .at Eine reguläre, invertierbare oder nichtsinguläre Matrix ist in der Mathematik eine quadratische Matrix, die eine Inverse . Die Rechtfertigung von der Invertierbaren zu sprechen wird durch Satz 16AV gegeben, wo gezeigt wird, dass es . Regularität dagegen sagt . Danach erfährst du, wie man einen reguläre Sprache Beweis durchführen kann und wie ein reguläre . ist genau dann regulär, wenn ist, d. BA=E B A = E, wobei E E die Einheitsmatrix ist. Submultiplikative Matrixnormen besitzen .Eine quadratische n-dimensionale Matrix A heißt unitär diagonalisierbar oder diagonalähnlich, wenn sie eine normale Matrix ist, deren Eigenwerte Elemente ihrer Grundmenge sind, oder; es eine Diagonalmatrix D gibt, zu der sie ähnlich ist, d.Eine Diagonalmatrix ist genau dann invertierbar, wenn alle Elemente der Hauptdiagonale von 0 verschieden sind. Rechenregeln für Matrizen. Die Gerschgorin Kreise machen lediglich eine Aussage über die Lokalisierung der Eigenwerte einer Matrix A. Die Determinante von ist dann gegeben durchLexikon der Mathematik LR-Zerlegung.Eine Matrix, wo AT = – A ist, nennt man Schiefsymmetrische Matrix. 10K views 6 years ago Videos zum Buch Lineare Algebra 1 aus der Buchreihe Angewandte Mathematik für Ingenieure Was sind reguläre Matrizen .Eine Matrix hoch minus 1 steht dabei für die inverse Matrix. Schließlich ist klar, daß die inverse Matrix der regulären Matrix regulär ist mit der inversen Matrix , denn es gilt . Darüber hinaus ist die Umkehrung einer Diagonalmatrix immer eine andere Diagonalmatrix mit den Umkehrungen der Hauptdiagonale:
Symmetrische Matrix
Eine n-reihige, quadratische Matrix A heisst regular, wenn ihre Determinante einen von Null verschiedenen Wert besitzt. x 1 = x 2 = x 3 = = 0 (ein beliebiges Lösungsverfahren, z. Lesezeit: 1 min Dr.Existiert für eine (quadratische) Matrix A eine inverse Matrix A -1 so nennt man A eine reguläre Matrix, andererseits nennt man A eine singuläre Matrix.Die Einheitsmatrix oder Identitätsmatrix ist in der Mathematik eine quadratische Matrix, deren Elemente auf der Hauptdiagonale eins und überall sonst null sind. Die Matrix ist eine quadratische Matrix.Der Spaltenrang einer Matrix sagt dir, wie viele linear unabhängige Spaltenvektoren du in der Matrix maximal finden kannst.
Rechenregeln für Matrizen
Reguläre Matrix
dass es eine reguläre Matrix S gibt, sodass S −1 AS eine Diagonalmatrix ist,:344 oder
Grundlagen der Matrix-Algebra
Deshalb wird folgender Weg gewählt: Für die Lösung des Gleichungssystems wird ein Verfahren benutzt, das nur für positiv definite . Die Lösung formt mit der gaussmethode die matrix so um, dass die Diagnose 0 ist, und leitet daraus die Forderung für r ab, damit diese auch 0 ergibt. Eine quadratische Matrix hat genauso viele Spalten wie Zeilen., deren Determinante Null ist.Eine reguläre, invertierbare oder nichtsinguläre Matrix ist in der Mathematik eine quadratische Matrix, die eine Inverse besitzt. Eine Matrixnorm ist in der Mathematik eine Norm auf dem Vektorraum der reellen oder komplexen Matrizen. Zum Beispiel zeichnen sich reguläre Matrizen dadurch aus, dass die durch sie beschriebene lineare Abbildung bijektiv ist.
Reguläre, Inverse und Orthogonale Matrix
die Zeilen- oder Spaltenvektoren linear unabhänig sind. Dies bedeutet: Eine beliebige (ggf. So eine ähnliche Regel gibt es auch für Matrizen.,) = ()Die Determinante wird auch .Eine Matrix ist genau dann regulär, wenn sie nur von 0 verschiedene Eigenwerte hat. Wann kann man eine Matrix diagonalisieren? Nicht alle Matrizen können diagonalisiert werden; Nur Matrizen, die bestimmte Eigenschaften erfüllen, können diagonalisiert werden.Sie ist symmetrisch, selbstinvers, idempotent und hat maximalen . Reguläre Matrizen können auf mehrere . Die Einheitsmatrix ist im Ring der quadratischen Matrizen das neutrale Element bezüglich der Matrizenmultiplikation. Da die Determinante ungleich 0 ist, hat die Matrix Maximalrang ist ist damit regulär.Für mehr Info gehe auf https://lernflix.Matrizen, die eine Inverse besitzen, sind immer quadratisch.MatrixdarstellungInverse MatrixRang Einer MatrixMatrixeigenschaftenOrthogonale Matrix
reguläre Matrix
Der erste Satz über reguläre Matrizen bezieht sich auf die durch sie gegebenen linearen . Definition Sei eine beliebige Matrix. Ob eine Matrix diagonalisierbar ist, lässt sich auf unterschiedliche Weise erkennen: Eine .Der Begriff Matrix ist in der linearen Algebra fast allgegenwärtig. Ist eine Matrix invertierbar, so .Die Definition einer singulären Matrix, auch entartete Matrix genannt, lautet wie folgt: Eine singuläre oder entartete Matrix ist eine quadratische Matrix, die nicht invertiert werden kann und deren Determinante daher gleich 0 ist.
Einheitsmatrix
Das Konzept lässt sich auf Endomorphismen übertragen.
Universität Karlsruhe (TH) Angewandte und Numerische Mathematik
Anmerkungen A is regulär, wenn det A = 0 ist, und singulär, wenn det A = 0 ist.
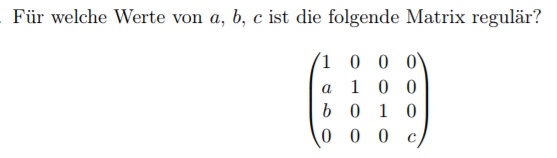
Inverse Matrix berechnen.Das ist die Matrix, bei der alle .
- Was Ist Eine U10-Vorsorgeuntersuchung?
- Was Ist Eine Komposition? – Musikkomposition
- Was Ist Eine Prom Chip _ Prom (Begriffsklärung)
- Was Ist Eine Rücknahmeerklärung Einer Kündigung?
- Was Ist Eine Kurdische Namensgebung?
- Was Ist Eine Lasagne? – Lasagne: So gelingt sie perfekt
- Was Ist Eine Mpu Prüfung , Medizinisch-Psychologische Untersuchung (MPU)
- Was Ist Eine Wärmeausdehnungskoeffiziente?
- Was Ist Eine Tourismuskauffrau?
- Was Ist Eine Verantwortung In Der Organisation?
- Was Ist Eine Myome Vergrößerte Gebärmutter?
- Was Ist Eine Verkaufsstrategie
- Was Ist Eine Out-Of-Home-Kampagne?