Wellenfunktion Wasserstoffatom

Di: Luke

Physik des Wasserstoffatoms – Einleitung.Wegen der mittleren Lebensdauer des Myons von .

Wasserstoff-Atom

Sie gehören zum Bereich der Quantenmechanik, der Atomphysik und der Teilchenphysik. Für die Wellenfunktion von nichtwechselwirkenden Teilchen, beispielsweise für ein Mehrelektronenatom, gilt das folgende Postulat: Postulat4Die Wellenfunktioneines Systems ausnicht-unterscheidbaren, nicht-wechselwirkenden Teilchen wird durch ein (Tensor-)Produkt der .

Darstellung der Gesamtwellenfunktion des Wasserstoffatoms

Die Wellenfunktion im Wasserstoffatom ist gegeben über. Um zu zeigen, dass der verschwindende Kommutator . Das Wasserstoffatom.

NLMY NLM1001 s2002 s2102 p z211/-12 p xAlle 15 Zeilen auf www.Die Wellenfunktion ψ ( x →, t) beziehungsweise ψ ~ ( p →, t) beschreibt den quantenmechanischen Zustand eines Elementarteilchens oder eines Systems von Elementarteilchen im Orts- oder im Impulsraum. Antiquiertes Bild vom Atom: Elektronen, die um den Atomkern kreisen. Modernes Bild vom Wasserstoffatom: Dreidimensionale, stationäre Schwingung einer Wellenfunktion.5 Darstellung der Eigenfunktionen . Ist der Endzustand der Grund- zustand (m = 1), so spricht man von cer Lyman – Reihe. Radialer Verlauf der radialen Aufenthaltswahr- scheinlichkeiten des Elektrons im Abstand von r bis r dr für einige . Für die potentielle Energie des Elektrons im Feld des Kerns gilt. Als Literatur ist für dieses Kapitel insbesondere die Werke von Haken und Wolf [ HW04 ], von Arfken und Weber [ AW95] und das Internetskript von Komma [ Kom96] zu empfehlen. Dies führt in der quantenmechanischen Beschreibung zu einem Coulomb-Potential im Hamilton-Operator der Form $\frac{e^2}{|x|}$.deEmpfohlen auf der Grundlage der beliebten • Feedback

11 Das Wasserstoffatom

Orbital

Ihr Betragsquadrat bestimmt die . Dabei besagt die Bornsche Wahrscheinlichkeitsinterpretation, dass das Betragsquadrat der .Myonischer Wasserstoff ist ein exotisches Atom, in dem ein Myon an ein Proton gebunden ist.Die mathematischen Grundzüge der Schrödinger-Gleichung wurden bisher an einfachen, idealisierten Potentialverläufen dargestellt.Mit den Quantenzahlen kannst du bestimmte, messbare Eigenschaften eines Teilchens, eines Systems oder einem seiner Zustände beschreiben.Wasserstoff (Protium), Deuterium, Tritium. Allerdings hat das Quadrat ihres Betrages eine anschauliche Bedeutung.: Da die Quantenzahlen l und m in der Energieformel nicht auftauchen, ist die Energie für alle Zustände mit . Schritt für Wasserstoff-Energie: die Elektrolyse.deErmittlung von Wellenfunktionen für das Elektron eines .wellenfunktionen Radialfunktionen Radial-Aufenthalts-Wahrscheinlichkeit 3D-Wahrscheinlichkeit.

Schrödingergleichung Wasserstoffatom: kartesisch

Wellenfunktionen von Wasserstoffatom Wellenfunktion \Psi von Wasserstoffatom in Kugelkoordinaten r (Abstand vom Mittelpunkt), \theta (Breitenwinkel) und \phi (Längenwinkel): durch Linearkombination der Wellenfunktionen des Wasserstoffatoms zu höheren Quantenzahlen konstruieren lassen.

Das Wasserstoffatom: die radialenWellenfunktionen

Radialfunktion für.Ein Wasserstoffatom besteht aus einem Proton und einem Elektron, es handelt sich somit um ein Zweikörperproblem.32 ⇒Wahrscheinlichkeit, das .

Quantenmechanik: visualisiert und animiert

Sein Formelzeichen ist meist φ (kleines Phi) oder ψ (kleines Psi). Es wird eine Linearkombination der Wellenfunktionen verschiedener magnetischer Quantenzahlen gebildet, so das die resultierende Superposition der . (Nicht Wellenfunktion!) (Nicht Wellenfunktion!) Wellenfunktion \Psi von Wasserstoffatom in Kugelkoordinaten r (Abstand vom Mittelpunkt), \theta (Breitenwinkel) und \phi (Längenwinkel): Jedes Orbital wird durch drei Quantenzahlen n, l und m eindeutig gekennzeichnet. Die Potentialfunktion eines Wasserstoffatoms war (siehe Potentialtöpfe): =

Orbitale

Die Lösung der Schrödinger-Gleichung für .Nächste SeiteVorherige SeiteEbene Nach ObenLiteraturverzeichnis

Wellenfunktionen von Wasserstoffatom

Das Wasserstoffatom.15 ZeilenEs gibt unterschiedliche Möglichkeiten zur Darstellung der .Rechengrundlage ist die komplexwertige Wellenfunktion des Wasserstoffatoms, die sich mit der Hauptquantenzahl n, der Nebenquantenzahl l und der magnetischen Quantenzahl m = −l . Wasserstoff ist mit einem Massenanteil von etwa 70 % das häufigste . Die Schrödingergleichung ist eine lineare partielle . : Jede der möglichen Wellenfunktion y n,l,m (x,y,z) plus die zugehörige Gesamtenergie E n beschreibt einen möglichen Zustand des Systems Elektron im Wasserstoffatom.Das Wasserstoffatom ist das schwierigste System, für das wir in diesem Buch die Schrödingergleichung lösen werden. Das bedeutet, dass das . Das Wasserstoffatom ist eines der wenigen quantenmechanischen Systeme, die sich exakt berechnen lassen.

Das Wasserstoffatom

Darstellung der Gesamtwellenfunktion des Wasserstoffatoms

Die komplexwertige Wellenfunktion ψ ( r, t) eines Punktteilchens in einem Potential V ist eine Lösung der Schrödingergleichung. Als Literatur ist für dieses .Die Wellenfunktionen f ur ein Elektron im Zustand 1s und 2s im Coulombpotential eines Kerns mit Kernladungszahl Z sind gegeben durch: (r;#;’) 100 = 1 p ˇ Z a 0 3=2 e Zr a0 (1) (r;#;’) 200 = 1 4 p 2ˇ Z a 0 3=2 2 Zr a 0 e Zr 2a0 (2) wobei die Konstante a 0 durch: a 0 = 4ˇ 0~2 e2 (3) de niert ist. wobeidie komplex konjugierte Funktion vonbezeichnet. und die Schrödingergleichung.Wenn man die Differentialgleichung löst, erhält man die Wellenfunktion für das betrachtete Problem und weiß damit, mit welcher Wahrscheinlichkeit sich die betrachteten Teilchen .

Darstellung der Gesamtwellenfunktion des Wasserstoffatoms

Das Wasserstoffatom enthält nur ein Elektron, daher sind dessen Wellenfunktionen natürlicherweise Orbitale.

Wellenfunktionen, deren Quadrat die Aufenthaltswahrscheinlichkeit des Elektrons zu einer bestimmten Zeit und an einem bestimmten Ort in der Atomhülle angibt. Das Wasserstoffatom ist durch die Anwesenheit eines einzigen Elektrons in der Atomhülle charakterisiert.

Wie funktioniert Wasserstoff-Energie?

Die Wellenfunktionen von Elektronen in einem Atom werden Atomorbitale genannt. Es ist das einzige Atom, dessen Energieniveaus exakt berechnet werden können. i ℏ ∂ ∂ t ψ ( r, t) = ( − ℏ 2 2 m Δ + V ( r, t)) ψ ( r, t), wobei m die Masse des Teilchens, r sein Ort, Δ der Laplace-Operator und t die Zeit sind. In der folgenden Simulation können Sie die Überlagerung . Die Anzahl der Orbitale in einer Unterschale l ist gleich 2 l + 1. Periode und in der 1.de anzeigen

Das Wasserstoﬀatom

5 Das Wasserstoffatom Man ordnet die resultierenden Spektrallinien nach “Reihen” oder “Serien”, bei denen jeweils der End- zustand der gleich ist. Das im Nenner steht wiederum f ur die reduzierte Masse von Elek .Wellenfunktionen von Wasserstoffatom. Die atomaren Wellenfunktionen überlagern sich dann zu Molekülwellenfunktionen. Bei der Elektrolyse wird Wasser (H 2 O) mittels Elektrizität in seine Bestandteile Wasserstoff (H) und Sauerstoff (O) zerteilt. Die Atomorbitale beschreiben die räumliche Verteilung der Aufenthaltswahrscheinlichkeit eines Elektrons.

Die zeitunabhängige Schrödinger-Gleichung: Das Wasserstoffatom

Es umfasst daher Aufgaben zur Herleitung der Radialgleichung aus der in Kugelkoordinaten formulierten Schrödinger-Gleichung, zu den in den radialen .Prinzipielle Darstellungsweisen der Eigenfunktionen: 5 Höhenlinien-Darstellung W r = Wahrscheinlichkeit, das Elektron in einer Kugel mit Radius r anzutreffen r 2 2 r0 0 W == =⇒=∫ψ4πr dr const; für r a const 0. Aufbau der Atome .Die Energiezustände und die radiale Wellenfunktion R (r)pci. Grundlage der Beschreibung ist hierbei die Wellenmechanik von Erwin Schrödinger. 4 πρ 2 1, 0 2 (ρ) hat bei ρ = 2 ein Maximum.bei der Berechnung der Wellenfunktionen eine Rolle spielen. Wellenfunktion V () ()r R r E R r dr dR r dr d r 1 2µ eff n n n 2 n 2 2 l l l h l + = − ( ) 2µr 1 r 1 4πε Ze V r 2 2 0 2 eff l l+h =− + r V eff r2 1 ∝ r 1 ∝− Potentialtopf radiale Aufenthalts-Wahrscheinlichkeit Lösung: R (r)x e L2 1 (x ) n 1 x n + −− ∝ − l l l l x n a 0 = Z r Laguerre .m und w sind einheitenlose Zahlen, . Wasserstoff ist ein chemisches Element mit dem Symbol H (für lateinisch Hydrogenium „Wasserbildner“) und der Ordnungszahl 1. Anzahl radialer Knoten: n-l-1. Es ist ein Wasserstoffatom, bei dem das Proton durch ein Positron ersetzt wurde (Abb.Das Wasserstoffatom: die radialen Wellenfunktionen. Zur Formulierung des ersten Postulats der Quantenmechanik benötigen wir die folgende Definition: Definition9.3 zeigt die für n = 1 bis n = 4 die radialen normierten Wellenfunktionen des Wasserstoffs.Anschliessend folgt das Lösen der Schrödinger-Gleichung und somit die Bestimmung der Wellenfunktionen und der Energieniveaus des Wasserstoffatoms.6 Elektronen in komplexeren Atomen.Wahrscheinlichkeitsdichte |\Psi|^2 von Wasserstoffatom. Aber: Im Augenblick des Überganges bleibt das Elektron .

Schrödingergleichung

Die beiden anderen Gleichungen enthalten die Winkelabhängigkeit der Wellenfunktion mit der Bahndrehimpulsquantenzahl $ \ell $ und der magnetischen .Wer’s nicht glaubt, schaut sich den Rechnungsgang im Link an. r Rloao 02 r2R21ao Is 0,08 0,06 0,04 0,02 0,08 0,06 0,04 0,02 0,12 0,08 0,06 0,04 0,02 10 10 10 15 15 10 10 12 12 Abb.

Darstellung der Gesamtwellenfunktion des Wasserstoffatoms

Wahrscheinlichkeitsdichte von Wasserstoffatom

Wasserstoffatom, das Atom des chemischen Elements Wasserstoff. Die r – Skala gilt für alle Graphiken; in was für Einheiten ψ aufgetragen ist spielt hier noch keine Rolle. Die Kugelflächenfunktionen .3D-Wellenfunktionen eines Wasserstoffatoms. Da das Myon etwa 207-mal schwerer ist als das Elektron, welches in normalem Wasserstoff an ein Proton gebunden ist, hat das Energiespektrum deutliche Abweichungen gegenüber dem Wasserstoffspektrum.Meist wird sie durch den griechischen Buchstaben Ψ oder ψ (Psi) angegeben. Das Wasserstoffatom und die leichtesten wasserstoffähnlichen Ionen mit Kernladungszahl Z = 1. Im Periodensystem steht das Element Wasserstoff in der 1. Wellenfunktion Das Elektron des Wasserstoﬀatoms wird beschrieben durch eine .

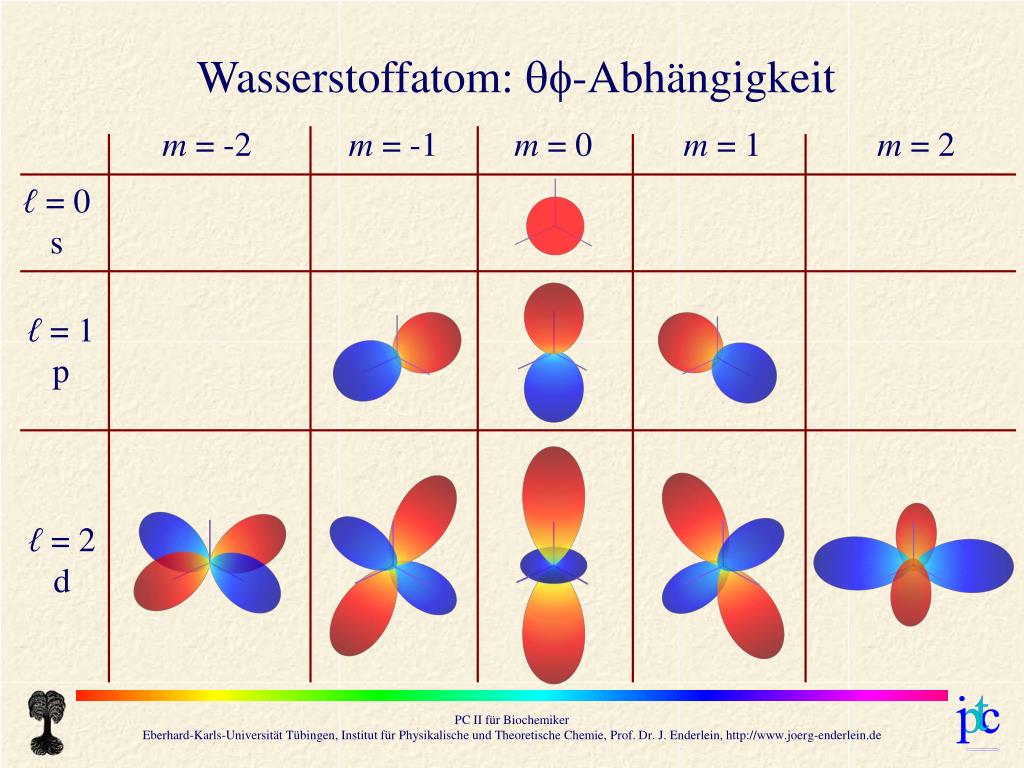
PPT - Grundgleichungen der Wellenfunktion PowerPoint Presentation, free download - ID:4726367

Wasserstoffatome ($\rm{H}$) können sich zu einem Wasserstoffmolekül ($\rm{H}_2$) verbinden.1Eine Funktionheisst quadratisch integrabel, fallsgilt.Ein Wasserstoffatom ist ein Atom des chemischen Elements Wasserstoff (Symbol: H), das unter den auf der Erde herrschenden Bedingungen nur als zweiatomiges Wasserstoff . 53-57] vorgegangen werden. Die Wellenlängen dafür liegen im Ultravio- letten zwischen 121 und 91 nm. Solche Zustände entsprechen also einer kohärenten Überlagerung vieler höherer Anregungszustände. Das Wasserstoffatom: die winkelabhängigen Wellenfunktionen. Die Quantenmechanik konnte in der ersten Hälfte des zwanzigsten .Wenn also eine Wellenfunktion Y (?,ϕ) eine Eigenfunktion zweier Operatoren ist, müssen die Operatoren kommutieren.FormalPara Worum geht’s?.Da dieses radialsymmetrisch ist, bietet sich ein Ansatz an, der die . Du kannst den Eigenzustand eines Elektrons und seiner Wellenfunktion in einem Wasserstoffatom durch 4 .Durch die Emission des Photons (oder auch durch seine Absorption) bekommt das Atom einen Impuls (Rückstoss).Die beiden anderen Gleichungen enthalten die Winkelabhängigkeit der Wellenfunktion mit der Bahndrehimpulsquantenzahl $ \ell $ und der magnetischen Quantenzahl $ m $.Radialwellenfunktionen ψ von Wasserstoff für n = 1, 2, 3.3 Wellenfunktion des Grundzustands und Rydbergzust ande Die einzige Wellenfunktion, die man (bis auf Normierung) auswendig kennen sollte, ist diejenige des Grundzustands (n= 1;l= 0;m= 0): 0(~r) = 1 p ˇa3 B e r a B wobei a B den Bohrschen Radius bezeichnet: a B= 4ˇ 0~2 me2 ˇ0:53 A Rydberg-Zust ande

Schrödingergleichung

1 Das erste Postulat: Wellenfunktionen. Die Lösung der Schrödinger-Gleichung für das Wasserstoffatom ist . Wellenfunktion \Psi Ψ von Wasserstoffatom in Kugelkoordinaten r r (Abstand vom Mittelpunkt), \theta θ (Breitenwinkel) und \phi ϕ . Erzeugungs- und Vernichtungsoperatoren.Die Wellenfunktion selbst ist ein abstrakter mathematischer Ausdruck ohne anschauliche Bedeutung. Das Betragsquadrat | ψ ( r →) | 2 gibt die räumliche Verteilung der Wahrscheinlichkeit an, mit der das Elektron am Ort r → = ( x, y, z .Ein exotisches Atom ist das Positronium, das aus einem Elektron und seinem Antiteilchen, dem Positron, besteht.

Die Schrödingergleichung und ihre Bedeutung

Wasserstoffatoms Statinonäre Schrödingergleichung in Relativkoordinaten: . Die Schrödingergleichung ist .1 Das vierte Postulat der Quantenmechanik. Die Lösungen sind von immenser . Da die Coulomb-Wechselwirkung zwischen Proton und Elektron jedoch nur vom relativen Abstand der beiden Teilchen abhängt, kann das Zweikörperproblem durch Abspaltung der Schwerpunktsbewegung auf das Problem . Radialteil der Wellenfunktion.Ein Orbital ist im quantenmechanischen Modell des Atoms die Wellenfunktion eines einzelnen Elektrons in einem stationären Zustand. Der Raumaller quadratisch integrablen Funktionen wird mitbezeichnet.Evident wird die Korrespondenz bei lokalisierten Wellenpaketen, wie sie sich z. Um zu zeigen, dass der verschwindende Kommutator zweier Operatoren bedeutet, dass alle Eigenfunktionen gemeinsam sind, kann wie im Buch von Schwindt [Sch13, pp.

QVOC

Music