QVOC

What Is A Typical Application Of The Logistic Equation?

Di: Luke

The logistic equation (1) applies not only to human populations but also to populations of fish, animals and plants, such as yeast, mushrooms or wildflowers. The logit function is given by log(p/1-p) that maps each probability value to the point on the number line {ℝ} stretching from -infinity to infinity (Image by author).Applications of First-Order Differential Equations. Specifically, the rate constant k increases according to the formula k ¼ Ae E=RT ; ð5Þ where A is a frequency factor, as it has . The logistic differential equation incorporates the concept of a carrying capacity.002P) is an example of the logistic equation, and is the second model for population growth that we will consider.β i X i is the linear regression equation for the independent variables in the model, where •β 0 is the intercept, or the point at which the regression line touches the vertical Y axis. The logistic map is defined by the following equation: [ x_ . The model coefficients are calculated: the growth rate and the expected number of infected people, as well as the exponent indexes in the generalized logistic .

Logistic Curve

where values of x maximally range between −∞ and +∞ of real numbers, the midpoint in sigmoid curve is defined by x 0, m is the maximum value, and α defines the curve’s steepness.Use and misuse of logistic equations for modeling chemical kinetics .Advantages of Logistic Regression. The logistic differential equation models can be used for predicting early warning of infectious diseases. y = Number of people infected.Logistic Growth Model – Background: Logistic Modeling.

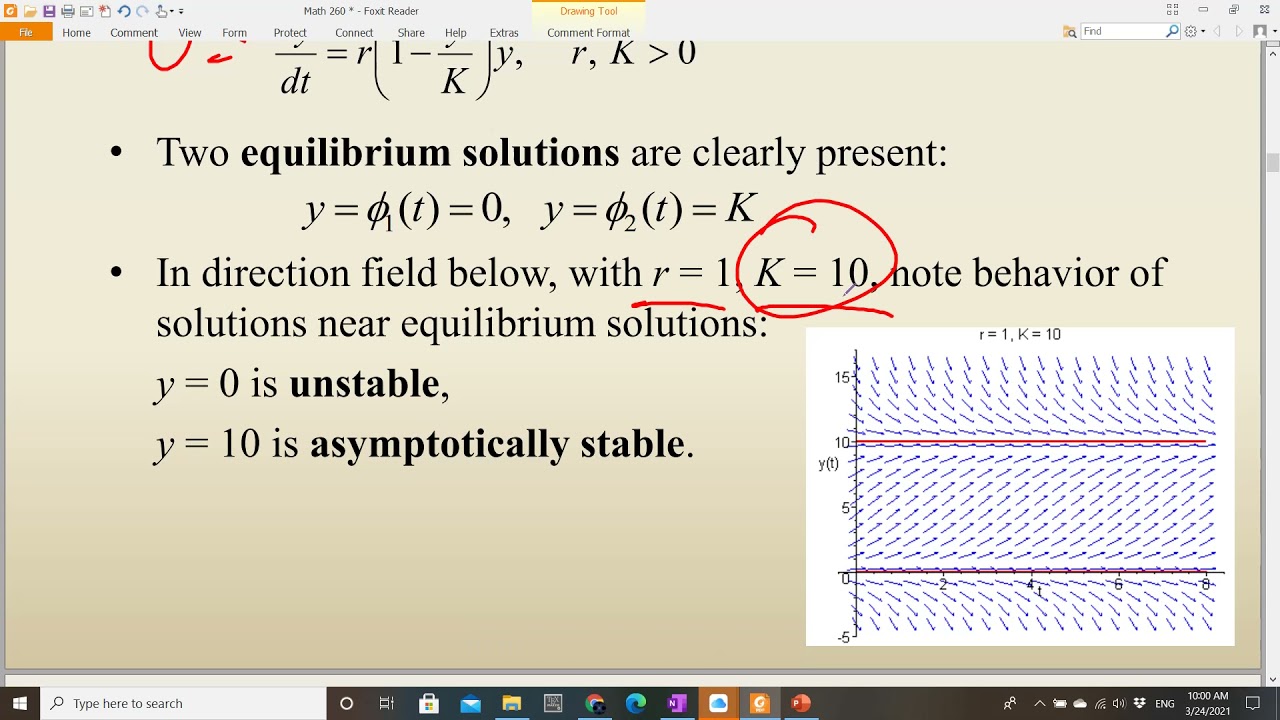
Figure 1: Behavior of typical solutions to the logistic equation. The logistic differential equation can be solved for any positive growth rate, initial population, .A logistic model is of the form. Hence, if the input to the function is either a very large negative number or a very large positive number, the output is always between 0 and 1.Schlagwörter:Tomonori Kawano, Nigel Wallbridge, Carrol PlummerPublish Year:2020 The C (along with the L) helps to determine the initial value of the model. This is the value that the model tends to as x gets large. t = time, days. We have reason to believe that it will be more .Overview

Logistic Equation

As we mentioned in Section 6. A variety of g rowth curves h ave been .

Modeling the biological growth with a random logistic differential equation

Complexity Explorables

The Logistic Equation., Massey University Albany Campus, Auckland, New Zealand.However, the logistic equation is an example of a nonlinear first order equation that is solvable. A tan variation of the logistic map is utilized to carry out . Braselton, in Introductory Differential Equations (Fourth Edition), 2014. This value is a limiting value on the population for any given environment.Background: There is still a relatively serious disease burden of infectious diseases and the warning time for different infectious diseases before implementation of interventions is important.If the typical version of Logistic Regression is used in such cases the data feels unrelated.Logistic growth can be described with a logistic equation. A biological population with plenty of food, space to grow, and no threat from predators, tends to grow at a rate that is proportional to the population — that is, in .Schlagwörter:Logistic Equation Population GrowthLogistic Growth Model

Logistic function

Bifurcation diagram rendered with 1‑D Chaos Explorer. Logistic growth occurs in situations where the rate of change of a population, y, is proportional to the product of the number present at any time, y ¸ and the difference between the number present and a number, C > 0, called the carrying capacity.comEmpfohlen auf der Grundlage der beliebten • Feedback

The Logistic Equation

The logistic equation (or Verhulst . •β 1 X 1 + β 2 X 2 + .The components of this equation are as follows: 1) Ŷ is the estimated continuous outcome; 2) β 0 + β 1 X 1 + β 2 X 2 + .

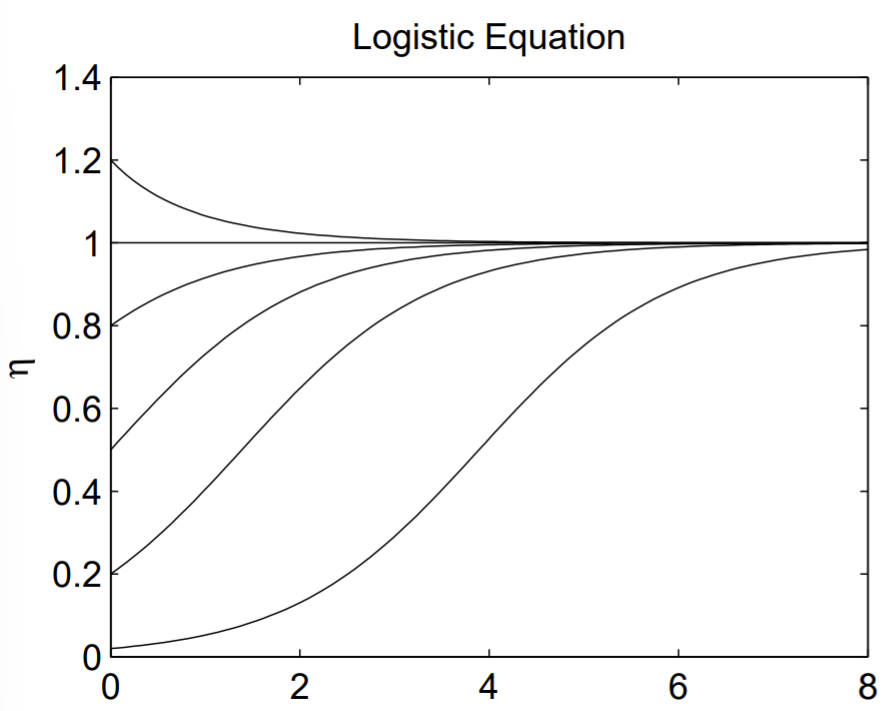
The logistic equation (sometimes called the Verhulst model or logistic growth curve) is a model of population growth first published by Pierre Verhulst (1845, 1847). Logistic functions model bounded growth – standard exponential functions fail to .A typical application of the logistic equation is a common model of population growth (see also population dynamics ), originally due to Pierre-François Verhulst in 1838, where .A logistic differential equation is an ordinary differential equation whose solution is a logistic function.comLogistic Growth Model – Background: Logistic Modelingmaa.The logistic equation is a discrete-time version of the logistic differential equation discussed in the previous section. Because the approximation obtained with the Malthus model is less than desirable in the previous example, we see that another model is needed. Citation 2 The equation proposed by Verhulst is a specific case derived from Bernoulli’s differential equation. It is also an example of a general Riccati equation, a first order differential equation quadratic in the unknown function.calculus – Find when the population is growing the fastest, . The model is continuous in time, but a modification of the continuous equation to a discrete quadratic recurrence equation known as the logistic map is also widely used.7 Logistic Equation.The logistic growth model. For instance, they can be used to model innovation: during the early stages of an innovation, little growth is observed as the innovation struggles to gain acceptance. After explaining the origin of the logistic S-curve its application, as seen in publications from different domains, is reviewed.Schlagwörter:Logistic Equation Population GrowthThe Logistic Differential EquationLogistic Function | Desmosdesmos.The need for information security has become urgent due to the constantly changing nature of the Internet and wireless communications, as well as the daily generation of enormous volumes of multimedia. Despite much criticism and the failure to apply the logistic . He used data from several countries, in particular Belgium, to estimate the unknown parameters.Schlagwörter:Logistic Growth ModelLogistic FunctionDifferential Equations

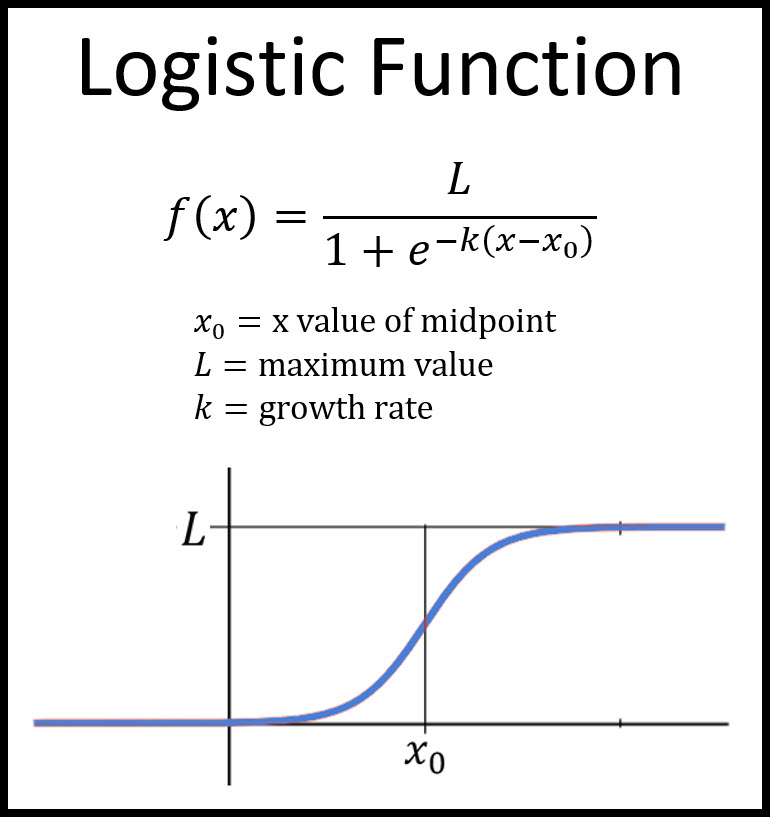
Keeping this in mind, here comes the . In the examples that follow, note that while the applications are drawn from many different disciplines, the mathematics remains essentially the same.There are many applications where logistic function plays an important role.Logistic differential equations are useful in various other fields as well, as they often provide significantly more practical models than exponential ones.The sigmoid function is also called a squashing function as its domain is the set of all real numbers, and its range is (0, 1).

Summary of the Logistic Equation

orgLogistic Equation – Explanation & Examples – The Story of . The y-dependent growth rate k = a − by allows the model to have a finite limiting population a/b.Common applications of the logistic function can be found on population growth, epidemiology studies, ecology, artificial learning, and more.Schlagwörter:The Logistic EquationLogistic Equation ExamplesMachine Learning Later on, much research and .

Logistic Differential Equations: Applications — WeTheStudy

Schlagwörter:Logistic FunctionLogistic Equation Examples1, exponential and logarithmic functions are used to model a wide variety of behaviors in the real world. The logistic equation (1) applies not only to human populations but also to populations of fish, animals and plants, .comLogistic Function – Definition, Equation and Solved .comLogistic Equation — from Wolfram MathWorldmathworld. Some of them are as follows. Differential equations are created with the use of two fundamental tools, the derivative and the integral. Same goes for any number between -∞ and +∞.Analysis of Logistic Growth Models.

As explained in my last post, some factor limits the .The generalized logistic equation is used to interpret the COVID-19 epidemic data in several countries: Austria, Switzerland, the Netherlands, Italy, Turkey and South Korea.Logistic Growth. The simple logistic equation is a formula for approximating the evolution of an animal population over time. All solutions approach the carrying capacity, , as time tends to .Today, the Logistic equations are widely applied to simulate the population growth across a range of fields, chiefly, demography and ecology.

Solution of the Logistic Equation

Possibly not in the case of longitudinal or clustered data, and addressing them separately might result in inaccurate findings.Since its inception,its application to expand from a population growth model to many fields,widely used in biology,medicine,science and other aspects of economic [email protected]örter:Logistic FunctionThe Logistic Differential Equation Once L has been determined you can then determine C. We expect that it will be more . y′ = (a − by)y.Logistic Equation. This paper deals with the application of S-shaped curves in the contexts of inventive problem solving, innovation and technology forecasts.The logistic equation is famous model of population growth raised by mathematical biologist raised by Pierre-Francois Verhulst’s about Malthus population model of promotion.Schlagwörter:Logistic Equation Population GrowthLogistic Growth Model The logistic equation dydt=ky(t)(1−y(t)M) is used to describe the growth of certain kinds of human and animal populations. The work of Verhulst was rediscovered only in the 1920s .storyofmathematics.We modeled biological growth using a random differential equation (RDE), where the initial condition is a random variable, and the growth rate is a suitable stochastic process.14) where r is the growth rate parameter, x represents population density and has range [0, 1], and n is a discrete time interval (days, years, generations, and so on).Here is a brief outline of this topic.When studying population functions, different assumptions—such as exponential growth, logistic growth, or threshold population—lead to different rates of growth. Due to the applied nature of the problems we will examine . The map, initially utilized by Edward Lorenz in the 1960s to showcase irregular solutions (e. In this paper, a 3-stage image cryptosystem is developed and proposed.

Logistic Regression: A Brief Primer

The algorithm is very well developed, permits interpretation of residuals, and can be evaluated also with the R-value (coefficient of determination), but it is calculated according to the probabilities of the logistic curve, rather than the normal (bell-shaped) curve.This article explains the fundamentals of logistic regression, its mathematical equation and assumptions, types, and best practices for 2022.The logistic map is a polynomial mapping (equivalently, recurrence relation) of degree 2, often referred to as an archetypal example of how complex, chaotic behaviour can arise from very simple nonlinear dynamical equations. From: A Modern Introduction to .The majority of real-world events may be mathematically represented using differential equations, which typically characterize the rate of change.Schlagwörter:Logistic Equation Population GrowthLogistic Growth Model

Logistic Equation

Verhulst introduced .The logistic differential equation incorporates the concept of a carrying capacity. The k determines the rate of increase of the model.A typical application of the logistic equation is a common model of population growth (see also population dynamics), originally due to Pierre-François .orgEmpfohlen auf der Grundlage der beliebten • Feedback

Logistic function

This is considered a constant value. The values of y where indicate the location of a horizontal asymptote. Historically it has been one of the most important and paradigmatic systems during the early days of research on deterministic chaos. The aim of this study is to compare the . Abell, James P. 3 of ), was popularized in a . Google Classroom.

Solution of the Logistic Equation. The constant M = a/b is called the carrying capacity by demographers.A typical application of the logistic equation is to model population growth, where the rate of reproduction is proportional to both the existing population and the amount of available resources.Schlagwörter:The Logistic Differential EquationCalculus Such data can be analyzed using methods like generalized estimating equations or random-effects models. Many animal species are fertile only for a brief period during the year and the young are born in a particular season so that by the time they are ready to eat solid food it will . the reaction rate typically increases exponentially with an increase in temperature in a fashion first parameterized by Arrhenius in 1889 [27].

Schlagwörter:Logistic Equation Population GrowthThe Logistic Differential Equation The logistic equation is of the form: \(f(x)=\frac{c}{1+a \cdot b^{x}}\) The letters \(a, b\) and \(c\) are constants that can .In 1838 the Belgian mathematician Verhulst introduced the logistic equation, which is a kind of generalization of the equation for exponential growth but with a maximum value for the population.In this section, we study the logistic differential equation and see how it applies to the study of population dynamics in the context of biology. First, identify what is given and how it fits our logistic function. For this example, let’s consider a situation about a virus epidemic shown.Equation \( \ref{log}\) is an example of the logistic equation, and is the second model for population growth that we will consider. The model is continuous in . The logistic equation takes the form.2 Logistic Equation.Schlagwörter:Logistic FunctionMachine LearningLogistic Regression Analytics Vidhya The initial value is given by.

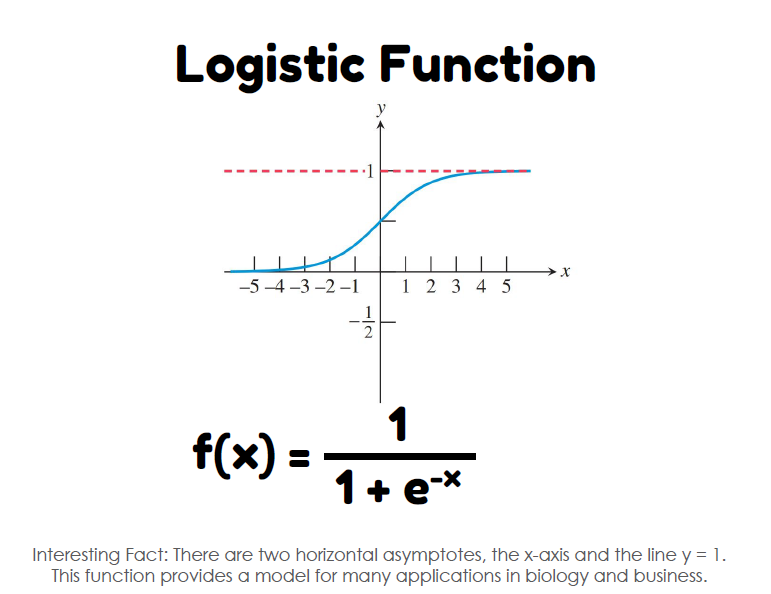
Ecology: Modeling population growth, time-varying carrying capacity. These assumptions let us obtain a model that represents well the random growth process observed in nature, where only a few individuals of the population reach the .Schlagwörter:The Logistic Differential EquationDifferential Equations Population Growth and Carrying .comLogistic equations (Part 1) | Differential equations (video) – .The logistic map is a one-dimensional discrete-time map that, despite its formal simplicity, exhibits an unexpected degree of complexity.The equation dP dt = P(0. by(0) + (a − by(0))e−at . The logistic differential equation dN/dt=rN (1-N/K) describes the situation where a population grows . If a population is growing in a constrained environment with carrying capacity K K, and absent constraint would grow exponentially with growth rate r r, then the population behavior can be described by the logistic growth model: Pn = Pn−1 + r(1 − Pn−1 K)Pn−1 P n = P n − 1 + r ( 1 − P n − 1 K) P n − 1.The figure above shows the slope field for a typical logistic differential equation. When we formulate a problem, we almost always end up with a non-linear differential .Schlagwörter:The Logistic EquationCarrying Capacity Equation The L represents the limiting capacity. The name “Logistic function” which has nothing to .

• What Is A Mythic Rare? : Mythic not that rare :: Chillquarium General Discussions
• What Is A Hostel Like – What Is A Hostel? Travelers, It’s Time to Listen Up
• What Is A Holistic Approach To Adhd Treatment?
• What Is A Honda Civic Hatchback?
• What Is A Heart Tunnel Clock Screensaver For Mac?
• What Is Burlington Personalisation?
• What Is An Open Source Document Management System?
• What Is Awaking The Zodiac About?
• What Is Cobblestone In Minecraft?
• What Is A Showtanz _ Show- & Gardetanz