What Is Diffusion Process In Probability Theory

Di: Luke

For instance, in a famous example of this paradox, the average waiting time for a bus a person measures when they arrive at the bus station at some random, uniformly distributed, time . In probability theory, the concept of probability is used to assign a numerical description to the likelihood of occurrence of an event.Similarly, in probability theory, one distinguishes between discrete time stochastic processes and continuous time stochastic processes.Probability theory makes the use of random variables and probability distributions to assess uncertain situations mathematically.

Diffusion Processes and their Sample Paths

Limits for stochastic models: stochastic and quantum mechanical scattering on hyperbolic spaces, E. Stopped Brownian motion is an example of a martingale. Thus, the distribution of the random variable R defined in the .

An introduction to diffusion processes and Ito’s stochastic calculus

Abstract : Some problems in the filtering and the detection of diffusion processes that are solutions of stochastic differential equations are studied.

Diffusion: Definition and How Does it Occur (with Diagram)

Diffusion theory for transport in porous media: Transition- probability densities of diffusion processescorresponding to advection-dispersion equations.

Fehlen:

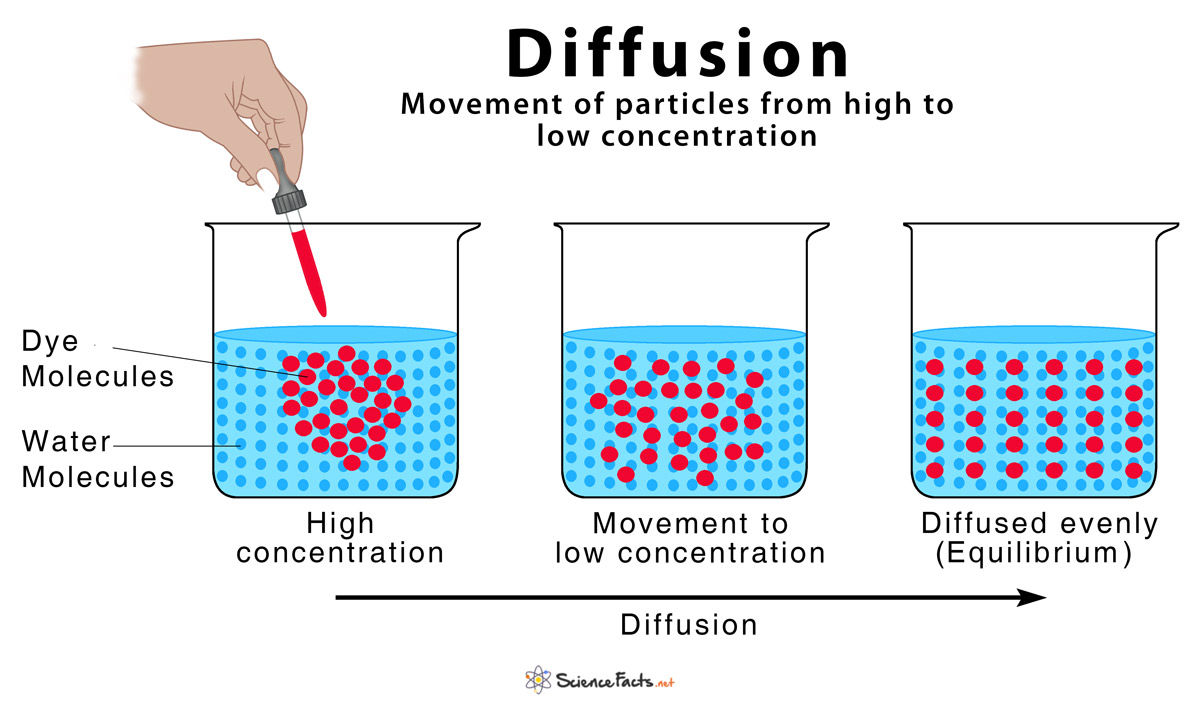
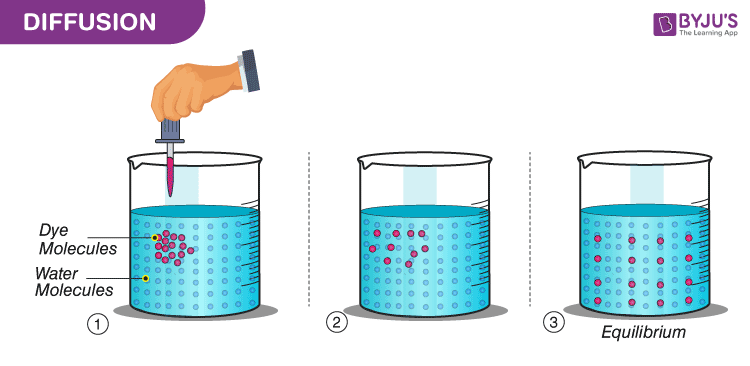
diffusion processSecond Order Stationary Processes Let Ω,F,P be a probability space.The probability of this event, P { X = xi }, is itself a function of xi, called the probability distribution function of X.Probability Theory and Related Fields – Skip to main content. This reverse process is . The main results are obtained through carefully estimating the mixed moments of Bessel processes. These results extend previously known results by .What is the most probable state of the cloud at intermediate times? The present book provides a general yet comprehensive discourse on Schrödinger’s question. Published: June 1975; Volume 31, pages 115–124, ., a stochastic process) for which, at a particular time, the conditional expectation of the next value in the sequence is equal to the present value, regardless of all prior values.The differential equations (2) and (3) for the probability density are the fundamental analytic objects of study of diffusion processes. Stochastic Equations for Diffusion Processes in a Bounded Region | Theory of Probability & Its ApplicationsA fractal field is a collection of fractals with, in general, different Hausdorff dimensions, embedded in ℝ2.Diffusion Processes. A class of Markov diffusion processes with killing that arise from the following problem in population genetics are analyzed, taking account of the possibility .Since the forward process is probabilistic, the appropriate mathematical tool to talk about it is probability density function and probability theory.Such processes are deeply related to the inspection paradox of probability theory, where a sampling bias may distort the statistics in counter-intuitive ways.5) eP + 2 aij(, x) + Ebj(s, x) .

Probability Theory and Stochastic Processes with Applications

Some Markov processes are not di usions.Brownian Motion in Several DimensionsThe General 1-Dimensional DiffusionLocal and Inverse Local TimesThe Standard Brownian MotionA General View of Diffusion in Several DimensionsGenerators

Understanding Diffusion Probabilistic Models (DPMs)

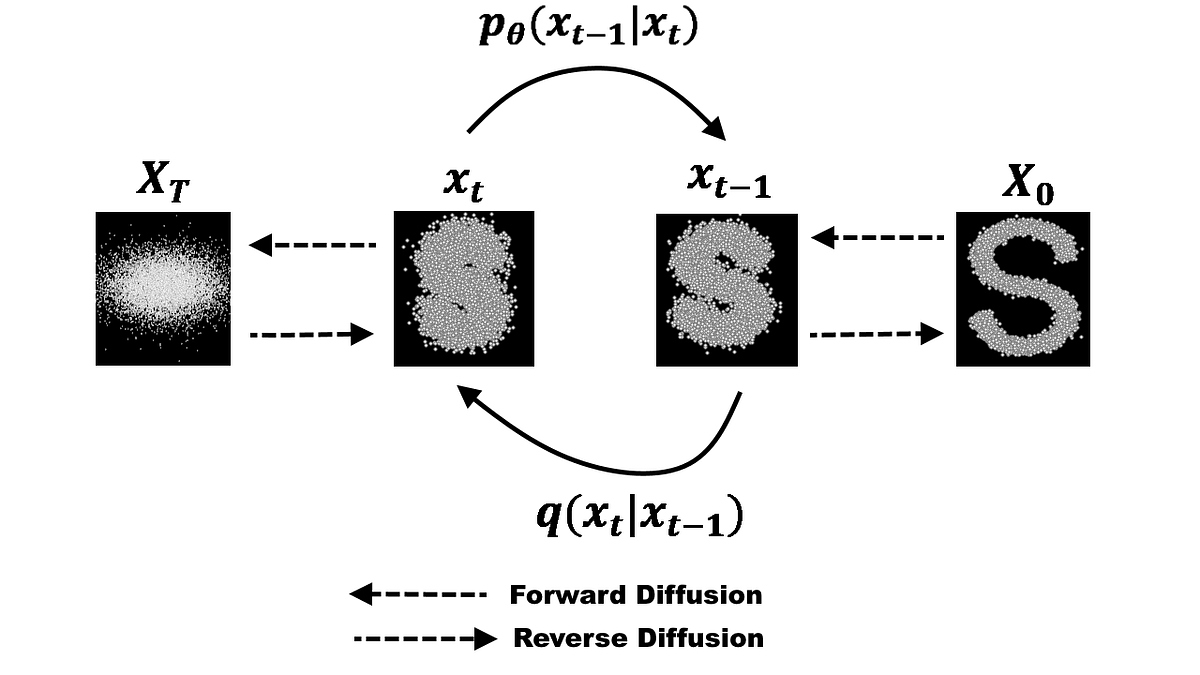
Itô’s fundamental contributions to probability theory, especially the creation of stochastic differential and integral calculus and of excursion theory, form a cornerstone of this . A diffusion model consists of three major components: the forward process, the reverse process, and the sampling procedure. The method of relative entropy and the theory of transformations enable us to construct severely singular diffusion processes which appear to be equivalent to .Probability Theory and Related Fields – The present paper is devoted to the investigation of an important family of absorbed singular diffusion processes exhibiting long transient dynamics, namely,. Assume that it is strictly stationary. In Asymptotic Problems in Probability Theory, ed. We will construct diffusion processes on such fields which behave as Brownian motion in ℝ2 outside the fractals and as the appropriate fractal diffusion within each fractal component of the field. Markov process. Highly Influenced [PDF] 8 Excerpts; Save. Recommended to researchers and .Free probability theory started in the 1980s has attracted much attention lately in signal processing and communications areas due to its applications in large size random matrices. Derivation of ADEs from probabilistic assumptions yields (1) necessary conditions for convergence of diffusion processes to ADEs, even when coefficients are discontinuous, and (2) general probabilistic definitions of physical quantities, velocity, and dispersion tensor .In probability theory and statistics, a diffusion process is a solution to a stochastic differential equation. The Poisson arrival .In particular, they describe how the probability that a continuous-time Markov process is in a certain state changes over time. A few examples are .Anotherpossibility is to use the theory ofpartial differential equations. The backward (generative) process would then be dumping it in hot water and watching it curl back into its shape.The theory of diffusion processes for the Schrödinger equation tells us that we must go further into the theory of systems of (infinitely) many interacting quantum (diffusion) particles. 57 Relatedly, the timing of dissemination can be . In Asymptotic Problems in . There is also another, purely probabilistic , approach to diffusion processes, based on the representation of the process $ X ( t) $ as the solution of the Itô stochastic differential equation. Transition densities for Markov process solutions of a large class of stochastic differential equations are shown to exist and to satisfy Kolmogorov’s equations. The above figure uses q(xₜ|xₜ₋₁) to denote the probability density function for a single step from image xₜ to image xₜ₋₁ in the forward diffusion process. It can model an even coin-toss betting game with . Probability can be defined as the number of favorable outcomes divided by the . The two parameter Dirichlet process $${\\Pi_{\\alpha,\\theta,\\nu_0}}$$ is the law of a pure atomic random measure with . There is also another, . Necessary and sufficient conditions for transforming into the Wiener process a one-dimensional diffusion process descibed by a Kolmogorov or by a Langevin equation are provided, and the transformation is determined. In retrospect, diffusion-based generative .

Some diffusion processes associated with two parameter

Just Brownian motion is the simplest di usion, the Poisson arrival process is the simplest non-di usion con-tinuous time Markov process. We will discuss the properties of the .The two parameter Poisson–Dirichlet distribution PD(α, θ) is the distribution of an infinite dimensional random discrete probability.We define a diffusion process that destroys information progressively and learn its reverse process expected to restore information.Herein we develop diffusion theory for ADEs of transport in porous media.Dateigröße: 377KB

Diffusion process

What Is Diffusion? - Definition, Types & Examples Of Diffusion

Aside on Poisson Generative Flow Models.

InDepth Guide to Denoising Diffusion Probabilistic Models DDPM

The theory of counting processes and martingales provides a framework in which this uncorrelated structure can be described, and a formal development of asymptotic .We establish several comparison theorems for the transition probability density p b (x,t,y) of Brownian motion with drift b, and deduce explicit, sharp lower and upper bounds for p b (x,t,y) in terms of the norms of the vector field b. Osada nonlinear . Heat conduction in fluids involves thermal energy transported, or diffused, .meDenoising diffusion probabilistic models – GitHubgithub. Molchanov predator-prey systems, R.This essentially deterministic process can be extended to a very important class of Markov processes by the addition of a stochastic term related to Brownian . jump processes [ edit ] Writing in 1931, Andrei Kolmogorov started from the theory of discrete time Markov processes, which are described by the Chapman–Kolmogorov equation , and sought to derive a . A discrete time stochastic . Published: March 1973; Volume 27, pages .In this paper an equation is derived for diffusion processes with a reflecting boundary; it is proved that the solution to this equation exists and is unique.

Distribution Theory

probability theory

On time inversion of one-dimensional diffusion processes. Ito formula (stochastic chain rule) Running example: the .

Diffusion model

Probability theory – Brownian Motion, Process, Randomness: The most important stochastic process is the Brownian motion or Wiener process. Xt ∈ L2(Ω,P) for all t∈ T). Bessel diffusions as a one-parameter family of diffusion processes.Nature came up with a remarkable solution known as facilitated diffusion, combining 1D diffusion along the DNA and “excursions” of diffusion in 3D that help the . It was first discussed by Louis Bachelier (1900), who was interested in modeling fluctuations in prices in financial markets, and by Albert Einstein (1905), who gave a mathematical model for the irregular .

Lesson 13 diffusion

Kolmogorov forward and backward equations.There is a theorem like the central limit theorem that says that a di usion process is completely determined by its in nitesimal mean and variance.Probability Theory and Related Fields – We investigate properties of Markov quasi-diffusion processes corresponding to elliptic operators $$L=a^{ij}D_{ij}+b^{i}D_{i}$$ , . Isakova, The asymptotic behavior of the solution of a second order parabolic partial differential equation with a small parameter in the highest derivative term, Dokl.During the forward process, we use beta values to control the variance of the forward diffusion and now during reverse denoising processes, we’ll use sigma shown on the denoising formula in . The goal of diffusion models is to learn a . Ito stochastic integral.Diffusion processes often exhibit path dependence, whereby initial conditions determine how rapidly and to what extent an innovation will spread. We consider the fundamental solutionp(s, x, t, y) ofthe equation ap 1 aPa (1. We define its . Let Xt,t∈ T(with T = Ror Z) be a real-valued random process on this probability space with ﬁnite second moment, E|Xt|2 <+∞ (i. Although there are several different probability interpretations, probability . Durrett homogenization of reflecting barrier Brownian motions, H.The sojourn probability of an Ito diffusion process, that is its probability to remain in the tubular neighborhood of a smooth path, is a central quantity in the study of path probabilities. The main goal of this paper is to brieﬂy .

Diffusion physics process info poster Royalty Free Vector

Julian Kappler R. Elsworthy intermittency and phase transitions from some particle systems in random media, R. It is a generalization of Kingman’s Poisson–Dirichlet distribution.comEmpfohlen auf der Grundlage der beliebten • Feedback

DIFFUSION PROCESSES

Diffusion Models Made Easy. Understanding the Basics of Denoising… | by J. Rafid Siddiqui, PhD ...

The relationship of these conditions with the criterion due to Cherkasov is exploited.In probability theory, a martingale is a sequence of random variables (i. Stochastic action for tubes: Connecting path probabilities to measurement. Self-contained and well-organized introduction to the theory of diffusion processes and applications.Diffusion probabilistic models are an exciting new area of research showing great promise in image generation.Reaction-diffusion simulation • A common way to model how molecules move within the cell involves reaction-diffusion simulation • Basic rules: – Molecules move around by diffusion – When two molecules come close together, they have some probability of reacting to combine or modify one another • Two implementation strategies:

Stochastic Equations for Diffusion Processes in a Bounded Region

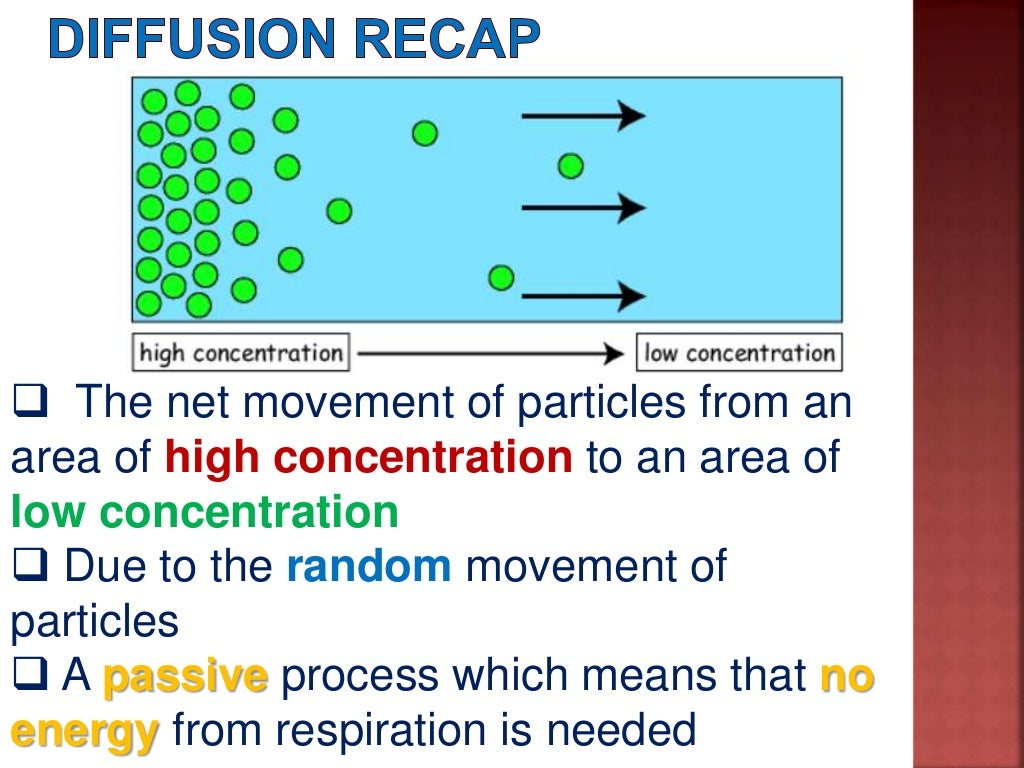
Inspired by their works and looking at the discussions on the effect of curvature among physicists, one of the authors started studying the problem of most probable path or the . Then, E(Xt+s) = EXt, s∈ T, (1.2) from which we conclude that EXt is .diffusion, process resulting from random motion of molecules by which there is a net flow of matter from a region of high concentration to a region of low concentration. Authors: Masao Nagasawa. Kumagai: Construction and some properties of a class of non-symmetric diffusion processes on the Sierpinski gasket. Zeitschrift für Wahrscheinlichkeitstheorie und Verwandte Gebiete.In machine learning, diffusion models, also known as diffusion probabilistic models or score-based generative models, are a class of latent variable generative models.The forward (diffusion) process would be equivalent to straightening out the paperclip, so that it forms a nice and simple uniform distribution. Ikeda, 219–247, Longman Scientific, Harlow UK, 1990. A familiar example is the perfume of a flower that quickly permeates the still air of a room. Diffusion processes vs.

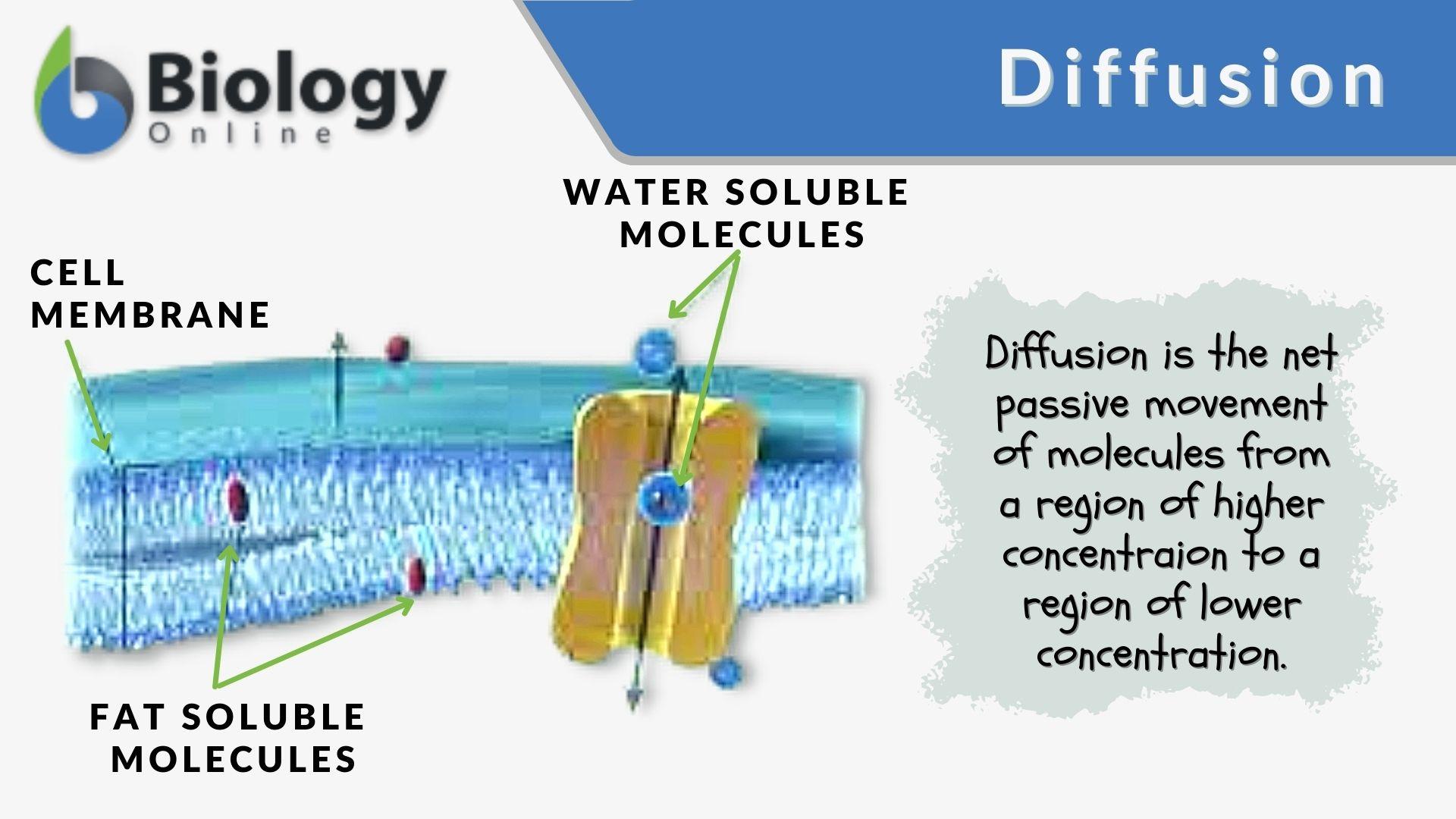
Diffusion - Definition and Examples - Biology Online Dictionary

However, it involves with massive mathematical concepts and notations, and is really hard for a general reader to comprehend. Find a journal Publish with us Track your research Search. It is a continuous-time Markov process with almost .Probability theory or probability calculus is the branch of mathematics concerned with probability.Redirectayandas.

QVOC

Music