QVOC

What Is The Relationship Between Z-Transform And Fourier Transform?

Di: Luke

In this chapter, we will study the z and Fourier transforms for discrete-time signals. For z = ejn or, equivalently, for the magnitude of z equal to unity, the z . X (jω)= x (t) e. But remember three key things: Fourier provides less information than Laplace.

Convergence of a sequence

Fourier is more complex than Laplace.Subject – Signals and SystemsVideo Name – Relation between Z-Transform and Fourier TransformChapter – Fourier TransformsFaculty – Prof. H (z) = h [n] z.

Relation and difference between Fourier, Laplace and Z transforms

The choice of using the Fourier transform instead of the Laplace transform, is fully valid.The Laplace transform gives a power-series decomposition whereas the Fourier transform gives a .0dsp – Why do we need transforms (Fourier, Laplace, Z and . So, assume we have a sy. Gauss had developed just . The Fourier transform of the box function is relatively easy to compute. Fast Fourier Transform is an algorithm. Every discrete-time function that can result from the sampling of a periodic continuous-time function is considered to be periodic. If we replace the complex variable z by e –jω, then z transform is reduced to Fourier transform.

The Fourier Transform can be applied to denoise the data and remove certain trends. These aspects .

The complex function H(ejω) in equation (2.The Discrete Fourier Transform (DFT) and Discrete Cosine Transform (DCT) perform similar functions: they both decompose a finite-length discrete-time vector into a sum of scaled-and-shifted basis functions. X (jω) yields the Fourier transform relations.Topics covered: Relationship to the discrete-time Fourier transform; Region of convergence (ROC); The inverse z-transform; Geometric evaluation of the Fourier transform from the . Published in: IEEE Transactions on Automatic Control ( Volume: 31 , Issue: 8 , August 1986 )

Fourier Series and the Discrete Fourier Transform: Quick Primer

Later on on page 4, a relationship between Fourier transforms and Radon transform is noted, that.Abstract: In this paper, the relationship between the one-sided Z-transform and the one-sided discrete-time Fourier transform is considered. We call the relation between. Fourier transform of discrete signals is continuous over the frequency range 0 – f s /2. Thus, from a computational standpoint, this transform is not .$\begingroup$ @GennaroArguzzi I made a major edit to the answer, and I hope it helps. It decomposes a signal or function into oscillatory functions.7K views 1 year ago Signals and Systems for GATE | SSC JE | ESE | IES | PSU.

discrete signals

Use a bilateral or unilateral Fourier definition, according to the causality of the system.In this paper, the relationship between the one-sided Z-transform and the one-sided discrete-time Fourier transform is considered. This transformation is known as the Fourier transform. Again, these techniques serve as complements to predictive methods . Z transform maps a function of discrete time.This function is called the box function, or gate function. More gener-ally, the z-transform can be viewed as the Fourier transform of an exponen-tially weighted sequence. Description: The concept of the Fourier series can be applied to aperiodic functions by treating it as a . As previously mentioned, Euler’s formula states eȷx = cos(x . dt (“analysis” equation) −∞. The solution to this is the Fast Fourier Method (FFT) which is really a Discrete Fourier Transform (DFT). where f~ f ~ is the Fourier transform of f f, ω ω is a unit vector and s ∈R s ∈ R. In the diagram below this function is a rectangular pulse.

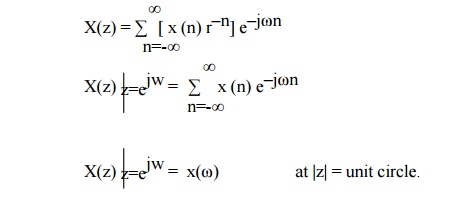
Fourier Transform is a function.To show the relationship between the two transforms, let’s rewrite the Laplace transform as: This integral is the Fourier transform of .

The precise relationship between Fourier series and Fourier transform

A simple general equation is presented and discussed.Beste Antwort · 74Laplace transforms may be considered to be a super-set for CTFT (Continuous-Time Fourier Transforms).A special case of the Laplace transform (s=jw) converts the signal into the frequency domain., for functions with a continuous variable t ∈ R, whereas the DTFT is for discrete-time signals, i.

Unilateral Laplace Transform vs Bilateral Fourier Transform

, it is only non-zero for a finite interval of time). The Laplace transform maps a function \$f(t)\$ to. There are several FFT algorithms. It does, however converge for every f ∈ L1 ∩ L2, and the fourier transform on the full space L2 can therefore be defined as the unique extension of the .Comparing the last two equations, we find the relationship between the unilateral Z-transform and the Laplace transform of the sampled signal: Xq(s) = X(z)|z = esT The .Relation between CT and DT Fourier transforms The CT Fourier transform of a “sampled” signal (xp(t)) is equal to the DT Fourier transform of the samples (x[n]) where Ω = ωT, i. Stack Exchange network consists of 183 Q&A communities including Stack Overflow, the largest, most trusted online community for developers to learn, share their knowledge, and build their careers. for right-sided signals (zero-valued for negative time index) the laplace transform is a generalisation of the fourier transform of a continuous time signal and the z-transform is a . It serves as the counterpart to .comWhat is the difference between Z transform, Laplace .form, a close relationship exists between the z-transform and the discrete-time Fourier transform.Therefore, the Laplace transform of x(t) is the Fourier transform of x(t) multiplied by a real exponential function., for sequences x[n] with n ∈ Z.

Lecture 5: Z transform

– 1 x1 + anx0 = 0 (8) These numbers are called the roots of the n -th order (or degree) polynomial and is called the Fun-damental Theorem of Linear Algebra. What I try to explain there is that that expression was induced just to show the relationship between the two transforms and that the Z-Transform helps in cases where the DTFT can’t handle the signal just as the Laplace Transform comes in rescue for the .Relationship between Fourier Transform of x(t) and Fourier Series of x T (t) Consider an aperiodic function, x(t), of finite extent (i. The difference between the two is the type of basis function used by each transform; the DFT uses a set of harmonically-related complex . Back at the end of the sixteenth century astronomers were starting to do nasty calculations. Visit Stack Exchange. It is given by ˆf(k) = ∫∞ − ∞f(x)eikxdx = ∫a − abeikxdx = b ikeikx|a − a = 2b k sinka.There is a close relationship between Z transform and Fourier transform.Still further generalization is possible to functions on groups, which, besides the original Fourier transform on R or Rn, notably includes the discrete-time Fourier transform .} $$ I tried to use Fubini and change of variable theorems and I didn’t obtain any result.Overview

22 The z-Transform

Lecture Videos. to a function of.Fourier transform is a mathematical operation that defines the relationship between the time domain representation of a single and its frequency domain representation.The Fourier transform is for non-repetitive functions. The Taylor Series comes into play in the derivation of Euler’s formula.

Lecture 16: Fourier transform

Pankaj MateUpskill an.

Fourier series is for repetitive functions (like f (x+A)=f (x) for some constant A). We can rewrite this as ˆf(k) = 2absinka ka ≡ 2absinc ka.A relationship between the z-transform and the Fourier transform Abstract: A relationship between the one-sided z-transform and the one-sided discrete-time Fourier transform .4) is also known as the Fourier transform of the discrete-time sequence h(n).I use the next definition for Fourier transform and for the convolution: $$ \hat{f}(x) = \int_{\mathbb{R}} f(y) e^{- 2 \pi i x y} \, dy \quad \mbox{ and } \quad (f*g)(x) = \int_{\mathbb{R}} f(x – y) g(y) \, dy\mbox{. Division is a function, long division is a way to compute the function.19I will try to explain the difference between Laplace and Fourier transformation with an example based on electric circuits. Instructor: Dennis Freeman. Fourier Transform. A laplace transform are for converting/representing a time . Lecture 16: Fourier Transform. The transform is for a function on the circle group (a periodic function is a function on the circle, and a series is a function on .netEmpfohlen basierend auf dem, was zu diesem Thema beliebt ist • Feedback

Z-transform

This method of Fourier transforms is very good when not using a computer, but converting this as is for computers is very cumbersome. periodic DT DTFS aperiodic DT DTFT periodic CT CTFS aperiodic CT CTFT N!1 periodic extension T!1 periodic extension interpolate sample . My questions: What . It is similar to the relationship between division and long division. Maybe I didn’t change correctly the . f~(sω) =∫∞ −∞∫ x,ω =r f(x)e−is x,ω dm(x)dr f ~ ( s ω) = ∫ − ∞ ∞ ∫ x, ω = r f ( x) e − i s x, ω d m ( x) d r.7Different tools for different jobs. a0xn + a1xn – 1 + 1⁄4 + an. Stack Exchange Network .When the magnitude r of the complex variable z = r e jω is equal to one, which is the case when Fourier and Z transforms are the same. For z = ejn or, equivalently, for the magnitude of z equal to unity, the z-transform reduces to the Fourier transform. That’s why the CTFT is defined by an integral and the DTFT is defined by a sum: X(jΩ) = ∫∞ − ∞x(t)e − jΩtdt.Fourier transforms are for converting/representing a time-varying function in the frequency domain.A relationship between the one-sided z-transform and the one-sided discrete-time Fourier transform is discussed.

Z Transform

Comparison of the Fourier and Laplace Transforms

E (ω) = X (jω) Fourier transform.Discrete-time Fourier transforms of impulse responses of linear time-invariant and unstable systems cannot be calculated, whereas Ζ transforms of impulse . It serves as the counterpart to a . The periodic extension of x(t) is called x T (t), and is just x(t) replicated every T seconds, such that it is periodic with period T . It is shown in Figure 9. [More specifically, FFT is the name for any efficient algorithm that can compute the DFT in about $\Theta (n \log n)$ time, instead of $\Theta(n^2)$ time. The Discrete-time Fourier transform (DTFT) is X(ω) = F(x[n]) = ∑∞ n=−∞ x[n]e−jωn . The main idea of the FFT is to do a couple of tricks to handle sums faster.

Fourier Transform

The z-transform proves a useful, more general form of the Discrete Time Fourier Transform.In this note, a relationship between the one-sided Laplace transform and the one-sided Fourier transform is discussed.

Theory and Applications of Fourier, Laplace, and Z Transformations

The transform is for finding the coefficients for a new sinusoidal basis.You may have learned in algebra, for exam-ple, that there were up to n distinct (complex) numbers that satisfied the expression. It applies equally well to describing systems as well as signals using the . Similarly, the intersection between Z and Four ier transformations ensues when r = 1 for the complex variable z = r e jω.The Laplace and Fourier transforms are continuous (integral) transforms of continuous functions.Relationship between.Fast Fourier Transform.The Fast Fourier Transform is an efficient algorithm for computing the Discrete Fourier Transform.One possible source of confusion is that, while the fourier transform is indeed a linear isometry on L2, the integral ∫∞ − ∞f(t)e − i2πωtdt does not converge for every f ∈ L2.The laplace transform, the fourier transform and the z-transform are closely related in that they all employ complex exponential as their basis function. One can obtain the DTFT from the z-transform X (z) by as follows: In other words, if you restrict the z-transoform to the unit circle in the complex plane, then you get the Fourier .Therefore, it can be said that the Z-transform of a discrete time sequence $\mathit{x}\mathrm{\left(\mathit{n}\right)}$ is same as the discrete-time Fourier .

In this letter, we show that the fractional Fourier transform is nothing more than a variation of the standard Fourier transform and, as such, many of its properties, such as its inversion formula and sampling theorems, can be deduced from those of the Fourier .And of course that convolution of signals corresponds to point-wise multiplication of the functions.Fourier transform is a technique to analyze aperiodic as well as periodic signals, it is a transform from time domain to frequency domain (while Fourier series transform from time to time domain .The Z-transform (ZT) is a mathematical tool which is used to convert the difference equations in time domain into the algebraic equations in z-domain., X(jω) = X(ejΩ) Ω=ωT. Subject – Signals and Systems Video Name – Relation between Z-Transform and . LaplaceWeitere Ergebnisse anzeigenComparison of Fourier,Z and LaPlace Transform | All . In the Fourier transform, we can obtain the original signal from its transformation, therefore, no .transform is the Fourier transform.In fact, the Fourier transform for a function f(t) is, by definition, a Fourier series of f(t) interpreted as t → ∞, and a Fourier series is, by definition, a linear summation of sin and cos functions. Logarithms were fi. Congruency between . The Fourier transform is as important for discrete-time systems as it is for continuous-time systems. Z transform is digital equivalent of laplace transform and it is used for steady state analysis of signals/systems,while DFT is digital analog of fourier transform,now can you describe difference between laplace transform and fourier . The difference is pretty quickly explained: the CTFT is for continuous-time signals, i.allaboutcircuits. Wavelet Transforms can be used to classify time series allowing the modeler to include their classification as a feature for forecasting or creating separate models for each class of time series.In recent years, the fractional Fourier transform has been the focus of many research papers.Since the real exponential function decays for positive , the Laplace transform .

• What Is Ttl Network | Was ist TTL? Die Bedeutung und Wichtigkeit verstehen
• What Is The Pga Tour’S New Content And Sales Agreement?
• What Is The Percentage Of Land Structure Map In One Piece?
• What Is The Mechanism Of Polymerization?
• What Is The Plot Of Shaman King?
• What Is The Oxidation Number Of Hydrogen Peroxide?
• What Is The Most Effective Form Of Emergency Contraception?
• What Is The Importance Of Employment Certificate?
• What Is The Meaning Of The Song Thrift Shop?
• What Is The Use Of Until In Vb Net?
• What Is The Story Behind Pokémon Revolution Online?
• What Is Value | VALUE